基于灰色马尔可夫模型的均值偏移算法
2013-09-17欧阳飒飒冀小平
欧阳飒飒,冀小平
(太原理工大学信息工程学院,山西太原 030024)
基于灰色马尔可夫模型的均值偏移算法
欧阳飒飒,冀小平
(太原理工大学信息工程学院,山西太原 030024)
针对Mean Shift算法中存在的不足,提出了结合均值偏移和灰色马尔可夫预测模型的目标跟踪算法。该方法利用灰色马尔可夫模型预测目标在当前时刻的中心位置,以此点作为均值偏移算法进行目标搜索的起始位置。同时,提取目标的几何特征,根据目标的面积来改善跟踪窗口的大小,利用“目标模型”和“候选模型”之间目标特征的变化产生模型更新策略。经实验得,该方法能实时稳健地进行跟踪。
Mean Shift;灰色马尔可夫预测模型;几何特征;目标跟踪
【本文献信息】欧阳飒飒,冀小平.基于灰色马尔可夫模型的均值偏移算法[J].电视技术,2013,37(3).
Comaniciu等[1]提出的基于Mean Shift的跟踪算法取得了很大成功,并且吸引了越来越多学者的研究兴趣。Mean Shift算法是一种非参数密度估算法,它具有良好的实时性,且对形变、目标遮掩的稳健性良好,易于与其他算法集成,广泛地应用于目标跟踪中。但该算法也存在一定的缺陷,为了解决传统均值偏移算法不能自适应改变核函数带宽的缺陷,Collins等将Lindeberg尺度的空间理论和Mean Shift算法相结合[2],并在某种程度上改善了此缺陷;Li Jinping等提出了采用Level Set描述目标轮廓方法与Mean Shift算法组合进行跟踪,使得在光线变化、目标颜色发生改变时取得好的效果[3],改善了相似颜色干扰问题;为了解决遮挡情况下均值偏移算法的跟踪缺陷,许多学者采用了目标预测结合Mean Shift的跟踪方法,Maggio E等提出了采用粒子滤波结合Mean Shift算法的跟踪[4],取得了好的跟踪效果,但计算量大。
本文在灰色GM(1,1)模型的基础上引入马尔可夫链预测理论,建立运动目标的灰色马尔可夫GM(1,1)预测模型,利用少量的数据来预测目标的运动轨迹,并以当前时刻的目标预测位置作为Mean Shift算法进行迭代搜索的起始位置;利用提取的几何特征表示相似度函数来自适应性地更新搜索窗口,以此减少迭代次数,最后根据模型更新策略来更新目标模拟。
1 Mean Shift算法
Mean Shift算法是一个自适应地寻找概率密度局部最大值的迭代方法。在目标跟踪中,采用归一化的加权颜色直方图来描述目标模型。假定跟踪目标的中心位于x0,xi是d维Euclidean空间Rd中的一组点,用向量表示xi(i=1,2,…,n),使用带宽为h的核函数K(x)作为多变量核密度估计,则目标模型可以表示为
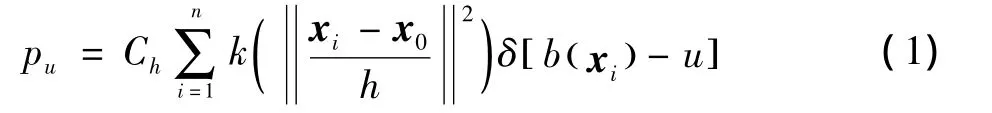

u个直方图,该函数值为1,否则为0。
令候选模型的中心坐标为y,则可以描述为
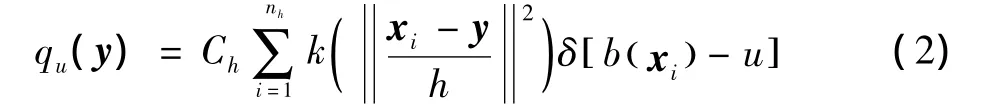
pu与qu(y)的相似性用Bhattacharyya系数^ρ(y)来度量,即
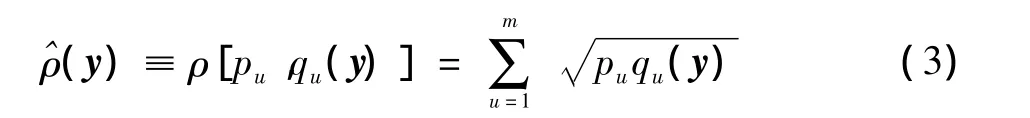
从式(3)可以看出,两个模型越相似,则^ρ(y)的值越大,为使其值最大,令yk表示目标的初始位置,将^ρ(y)在该点进行一阶泰勒展开求导为零,可以得到Mean Shift向量
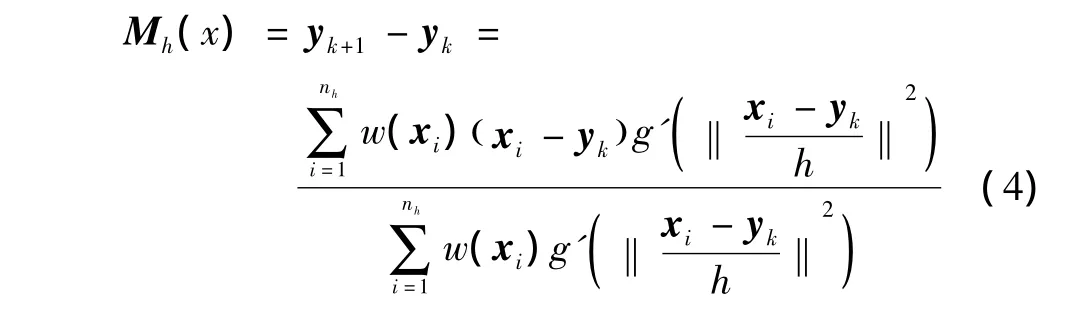

2 灰色马尔可夫预测模型
灰色系统预测的概念是由邓聚龙教授首先在国内提出,之后灰色系统理论的研究得到了迅速发展。灰色预测方法的优点在于对缺少基础资料的预测能够得到较好的预测效果,与别的预测方法相比较而言它用到的样本数据较小,而预测的精度相对较高。马尔可夫概率矩阵是对随机过程每个时刻状态的描述,它是根据状态之间的转移概率来预测系统的发展,把在不相同状态范围的内在波动规律展现出来,使随机作用造成的波动得以修正。灰色马尔可夫预测模型就是将两者的优势相结合进行预测。
2.1 建立 GM(1,1)模型
假设有原始序列为

将该序列x(0)进行一次累加生成处理,得到x(1)(记作1-AGO)
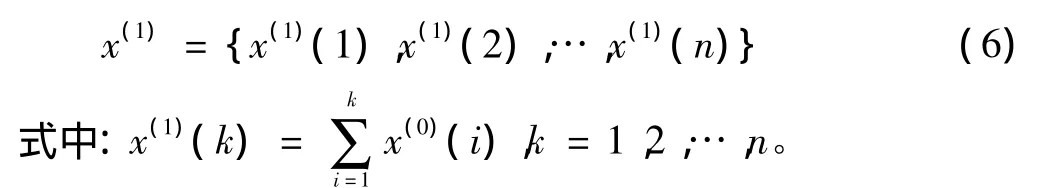
建立GM(1,1)灰微分方程

式中:a为发展系数;b为灰作用量,是待估参数。
把式(7)转化为矩阵方程


GM(1,1)模型的离散响应方程为
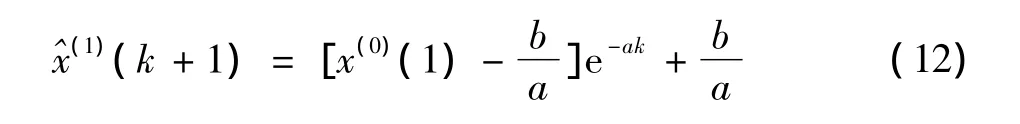
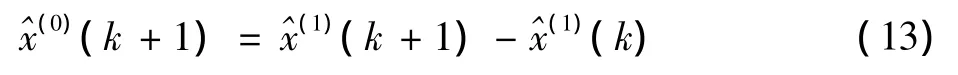
2.2 建立转移概率矩阵


由状态i经k步转到状态j的频率也可以用式(14)来表示,将状态转移概率依次排序,可得到矩阵
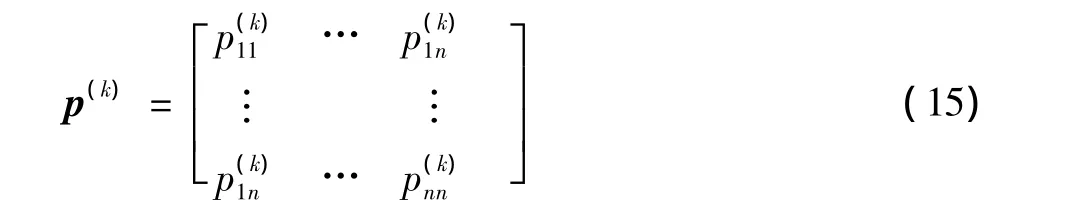

从以上分析可知,灰色GM(1,1)模型用来预测目标轨迹变化的总趋势,对其轨迹状态的修正则是通过马尔可夫转移概率矩阵来完成的,最终精确地预测出目标的位置,为均值偏移算法提供搜索初始位置,避免了由于遮挡造成的目标丢失。
3 Mean Shift算法和灰色马尔可夫模型的结合
跟踪的过程中,会产生一系列的时间序列{yi},i=1,2,…,表示迭代的次数,这种时间序列有平稳收敛(呈递增和递减两种形式分布)和波动收敛(呈交替状分布)两种形式。针对这两种形式,可以采用灰色马尔可夫模型进行目标中心位置的预测。在Mean Shift搜索之前先进行目标在下一帧中位置的初步预测,并用预测中心位置作为目标搜索的起始位置,之后再进行迭代搜索,不仅可以提高搜索准确性,还能够减少迭代搜索次数。灰色马尔可夫模型采用“新陈代谢”更新策略,保证用于预测的数据是最新的,一般用当前帧的前4帧数据作为基本数据,既保证了预测的准确性,也减少计算量。
如图1所示,提取的颜色特征用于传统的Mean Shift算法进行迭代计算,找出最匹配的目标位置,具体过程见本文第2节;利用文献[6]中的迭代投影算法来近视计算目标的面积,通过前后两帧面积的差值来判断是否更新跟踪窗口的大小;再设置一个阀值,根据相邻两帧的目标面积的比值是否小于阀值来判断是否更新目标模型,避免了目标模型过更新。
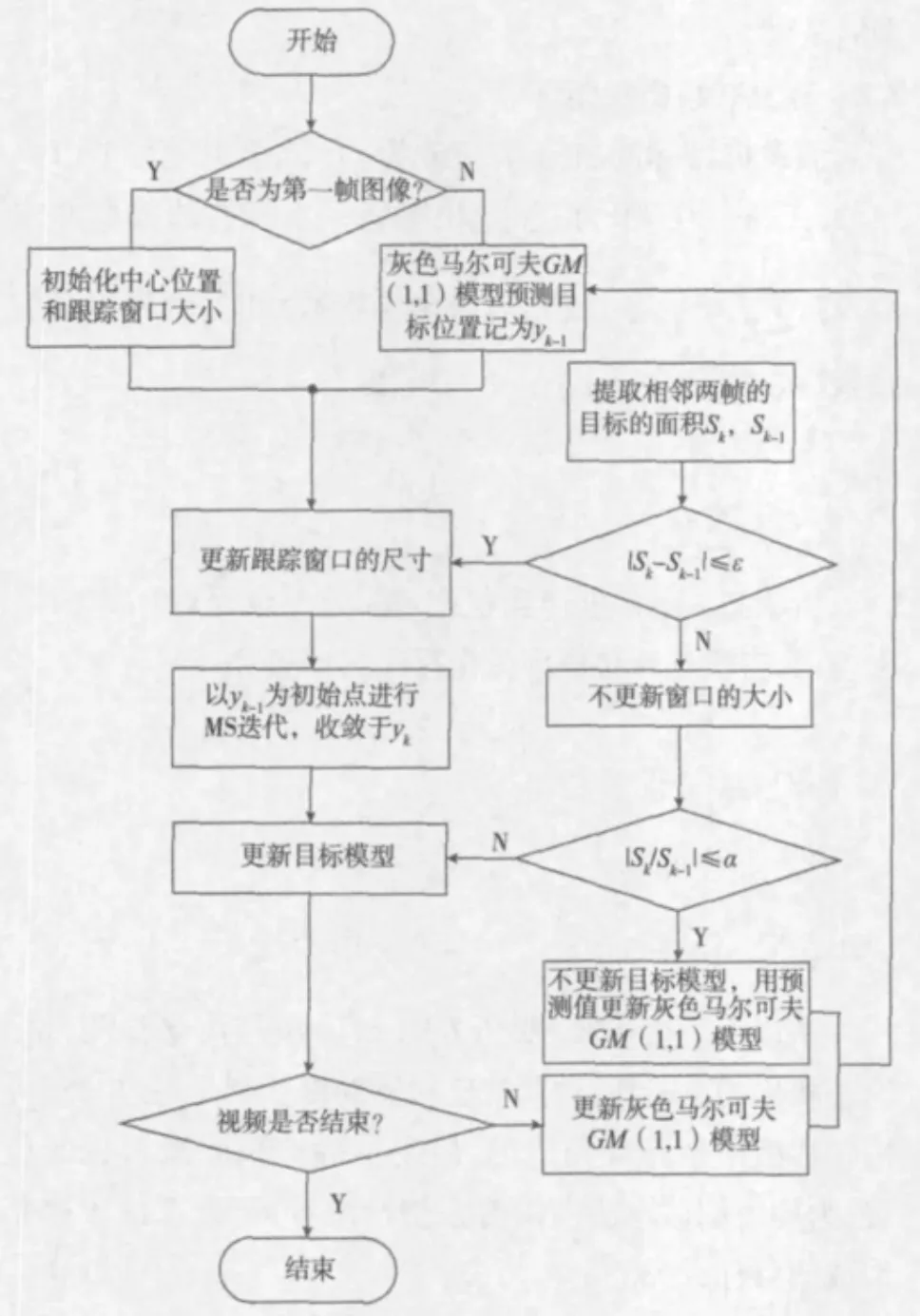
图1 本文算法流程图
4 实验结果与分析
本文实验使用的硬件平台为2.53 GHz的CPU、2 Gbyte内存,在Windows7操作系统下的计算机,软件平台为MATLAB 2010a编程环境。测试视频选取一段橄榄球的运动视频序列,视频图像大小为352×288,共88帧。根据反复的实验,选取模板更新阈值为0.2。在整个视频序列中,橄榄球的运动都是随机波动的,前42帧被跟踪的橄榄球从大到小,再从小到大,其大小一直在不断变化;后40多帧发生遮挡情况。
图2为传统的均值偏移算法跟踪的仿真图,当球的大小不断变化时,跟踪窗口不能自适应地调整大小,当球快速运动时,目标窗口的中心位置严重偏移,在42帧发生遮挡时,跟踪失败,跟踪窗口停留在第42帧时的位置。本文算法的仿真图如图3所示,根据灰色马尔可夫模型和均值偏移算法相结合,在球快速运动时能准确地确定目标的中心位置,再根据提取目标的几何特征的变化来改善跟踪窗口的大小,能很好地进行实施跟踪,效果也比传统的均值偏移算法要好;在发生遮挡时,以灰色马尔可夫GM(1,1)的预测值为中心来开窗,避免丢失跟踪目标。从两个仿真图来看,本文提出的算法要优于传统的均值偏移算法,可以取得良好的实时性和稳健性。

5 结论
当在运动目标跟踪的过程中,发生遮挡、多种运动方式存在的情况下,本文提出通过灰色GM(1,1)模型对目标的运动轨迹进行总趋势预测,再用马尔可夫概率转移矩阵来对轨迹进行修正,这样能准确预测出目标在每一帧中的中心位置,并比一般的预测方法计算量小、精度高;再结合Mean Shift算法进行匹配跟踪,最终确定目标。其中通过提取的几何特征的变化来更新跟踪窗口和目标模型,这样可以适应目标的尺度变化和避免了目标模型的过更新。实验表明,该方法能够对目标进行实时有效的跟踪。
:
[1]COMANICIU D,RAMESH V,MEER P.Real-time tracking of non-rigid objects using mean Shift[C]//Proc.IEEE Conference on Computer Vision and Pattern Recognition 2000.[S.l.]:IEEE Press,2000:142-149.
[2]COLLINS R T.Mean Shift blob tracking through scale space[C]//Proc.IEEE Conference on Computer Vision and Pattern Recognition 2003.[S.l.]:IEEE Press,2003:234-240.
[3]LI J P,LI Q J.Real-time tracking by combining level set and Mean Shift[J].Journal of Information & Computational Science,2008,5(2):829-836.
[4]MAGGIO E,CAVALLARO A.Hybrid particle filter and mean shift tracker with adaptive transition model[C]//Proc.ICASSP 2005.[S.l.]:IEEE Press,2005:221-224.
[5]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1992.
[6]叶有时,唐林波,赵保军,等.基于SOPC的深空目标实时跟踪系统[J].系统工程与电子技术,2009,31(12):3002-3006.
Grey Markov Model-based Mean Shift Algorithm
OUYANG Sasa,JI Xiaoping
(Collge of Information Engineering,Taiyuan University of Technology,Taiyuan 030024,China)
According to the existing shortcomings of Mean Shift algorithm,a combination of Mean Shift and the grey Markov forecasting model of the target tracking algorithm is presented.The method utilizes the gray Markov model to predict the center of the target at the present time,and this point is used for a starting position of the tracking window in the Mean Shift algorithm.Meanwhile,a geometric characteristics of the target is extracted.And then,the size of the tracking window is resized on the basis of the target area.The target characteristics’change between the target model and the candidate model is used to produce the model update strategy.By means of experiments,the method is validated to have a good real-time and robustness.
Mean Shift;Grey Markov forecasting model;geometric characteristics;target tracking
TP911.73;TP391.4
A
责任编辑:时 雯
2012-07-23
