基于GEM算法的地铁车站乘客疏散能力研究

许文超 周磊山

(北京交通大学交通运输学院 北京 100044)

基于GEM算法的地铁车站乘客疏散能力研究

许文超 周磊山

(北京交通大学交通运输学院 北京 100044)

为分析和提高地铁车站通过设施的疏散能力，保证乘客的运行安全，在分析地铁车站行人流运动特性的基础上，利用GEM(generalized expansion method)算法，求解地铁车站乘客疏散模型，通过计算得到车站疏散设施的拥堵概率、吞吐量等指标，给出地铁车站疏散能力的瓶颈点。以西直门地铁站为案例，证明将GEM算法应用于解决地铁车站人员疏散问题的可行性，并在此基础上提出合理的进站线路疏散优化方案。

地铁车站;乘客;疏散能力;GEM算法

对于现代化的都市而言，地铁的运营在很大程度上缓解了地面交通的拥堵状况。然而，随着市民出行需求的增长及地铁通行能力的限制，地铁站各疏散设施在高峰时段极易形成拥堵。地铁作为城市交通的重要组成部分，如何保证乘客的生命财产安全，提高地铁站内设施的疏散能力成为地铁运输组织工作中的重中之重［1］。

国内外很多学者对于拥堵的疏散问题进行了深入的研究，文献［2］在分析拓扑结构的基础上，提出了通过计算机仿真结构来计算拓扑结构网中拥堵问题的相关变量的算法;文献［3］在此基础上加以扩展，应用一般扩展节点分析法来分析和解决拥堵问题;文献4在M/G/c/c排队模型的基础上，提出了相关网络排队模型。国内的学者在人员疏散问题上也做出了一定的贡献，如方正等提出的空间网格疏散模型［5］;宋卫国教授等提出了社会力模型，并对实际疏散中出现的某些现象进行模拟［6］等。

在诸多研究中，国内学者针对地铁站楼梯、通道等疏散设施衔接性疏解的问题研究较少，且尚没有应用GEM(Generalized Expansion Method)算法求解人员疏散模型的先例，GEM算法可以方便地达到输入疏散设施及乘客运动特性数据，即可输出地铁站疏散设施拥堵指标的功能，为进一步研究人员疏散提供依据。笔者以北京市西直门地铁站为例，针对地铁站的人员疏散问题，以行人流运动特性分析为基础，利用GEM算法求解M/G/c/c排队模型，并利用调研得到的数据计算、分析地铁站疏散设施的瓶颈点，最后针对瓶颈点提出相应的疏散优化方案。

1 地铁站行人流特性分析

楼梯和通道作为疏散地铁行人流的主要站内设施，是影响行人通过时间、通过能力以及疏散过程中的运输组织效率的重要环节。分析行人流在楼梯、通道内的运动特性是研究地铁站拥堵状况及其瓶颈点产生的基础［7］。

结合地铁站的空间结构特点，将地铁站拆分成通道、楼梯等基本单元，通过采集的基本单元的长度、宽度等物理参数以及行人在基本单元内部的运动特性数据，得到基本单元行人流的速度-密度关系散点图，依据格林希尔茨(Greenshields)提出的交通流理论公式

(vf为畅行速度，kj为阻塞密度)构建每个基本单元的行人流速度-密度拟合曲线图，通过曲线拟合趋势分析各楼梯、通道内行人流的运动特性，得到地铁站行人流运动速度随行人密度变化的关系，为构建地铁车站疏散能力瓶颈的分析模型提供支持。

2 地铁车站疏散模型与算法设计

乘客在地铁站通道、楼梯等基本单元中因运动而产生的排队及拥堵，可看成是满足某些特征的排队活动。以基本单元为服务台，乘客的运动特性可以通过排队系统内部的各物理参数进行描述。

2.1 模型建立

通过计算、分析调研获得的数据，采用M/G/c/c排队模型描述西直门地铁站乘客运动特性［8］。M/G/c/c排队模型是指满足乘客到达间隔时间服从负指数分布、服务时间服从一般服务时间的分布、系统容量和乘客到达量有限、先到先服务的单服务台排队模型。

定义如下符号和变量:c为基本单元最大容纳人数;l为基本单元长度，m;w为基本单元宽度，m;vn为基本单元内有n个乘客行走时的平均速度，m/s;v1为基本单元内乘客行走的自然速度，m/s;va和vb分别为基本单元内乘客密度为2人/m2及4人/m2时乘客的平均行走速度，m/s;γ和β为指数模型参数;λ为基本单元内乘客的到达率，人/s;N为基本单元内乘客的随机数量，人;E［T1］为乘客自然行走时的期望服务时间，s，即 E［T1］=l/v1;f(n)表示楼梯或通道中第n位乘客的服务率。

2.2 模型求解

2.2.1 GEM 算法设计

利用单节点GEM算法求解M/G/c/c排队模型。

GEM算法是基于离散事件仿真模型的一种算法，该算法将地铁站内楼梯及通道等基本单元看成依次连接的有通过能力的节点，并将各个节点分别等效为一个长方体水平通道，假设水平通道内行人流的到达率为λ，行人流在节点内运动时，节点内共有n个乘客时的行人流速度可近似为

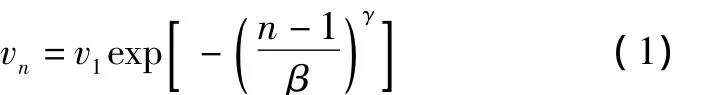
则有n个乘客行走时基本单元的拥堵概率为

其中，P(0)为基本单元中没有乘客的概率，即

其他描述排队系统物理特性的指标为

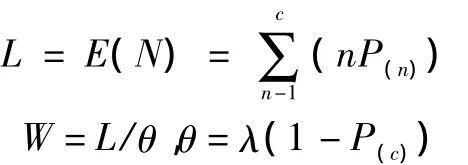
其中，L为基本单元内的期望乘客人数，即E(N);W为期望服务时间，s;θ为基本单元吞吐量，人/s;P(c)为乘客数量达到或超过基本单元最大容纳人数时发生阻塞的概率。

2.2.2 GEM 算法步骤

文献［8］的研究表明，当行人流密度达到5人/m2时，行人流的运动速度较小，取基本单元的最大容纳人数c=5lw，对行人运动速度及基本单元参数赋值:

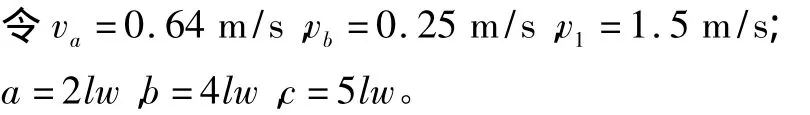
其中a和b依次表示行人流密度为2人/m2和4人/m2时基本单元的容纳人数，则单节点GEM算法流程为

步骤1:数据初始化，其中n［－1］=1，sum=1

2.2.3 GEM 算法程序

利用Mathematica软件的符号编程语言，将GEM算法封装成一个与节点内乘客的到达率、节点长度及宽度有关的函数，通过与用户的交互，实现用户通过输入节点内乘客的到达率、节点长度及宽度等数据，即可在程序指定区域输出节点的拥堵概率、吞吐量、排队的队长及排队等待时间等指标的功能。

此外，用户通过改变乘客到达率，利用此程序实时输出节点的拥堵概率随到达率变化的曲线，其中斜率变化最大的点，即为通道能力的瓶颈点，如图1所示。

图1 节点拥堵概率随到达率变化的曲线

3 案例分析

北京市西直门地铁站是地铁2号线、4号线和13号线交会的重要换乘车站，其周边地带经济繁华，大量的出行和到达客流量已经大大超过了地铁站的设计通行能力，给乘客出行带来了极大的阻碍。以西直门地铁站作为研究对象，应用GEM算法求解M/G/c/c排队模型，得到西直门地铁站疏散能力的瓶颈点，并根据实际情况提出相应的优化方案。西直门地铁站的站内结构如图2所示。

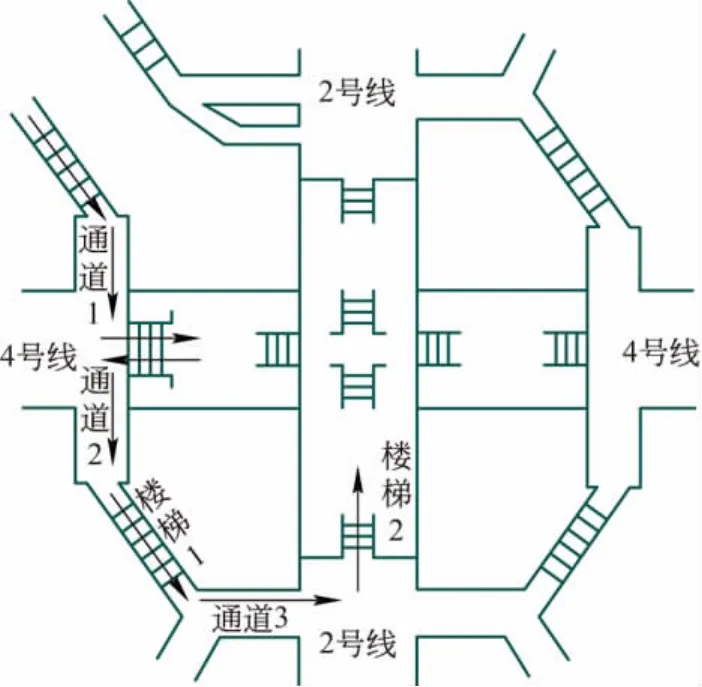
图2 西直门地铁站站内结构

3.1 地铁站行人流速度-密度函数关系

将西直门地铁站拆分成通道、楼梯等基本单元，选取图2所示进站线路的2个楼梯和3个通道作为研究对象，按照乘客经由通道1、通道2、楼梯1、通道3、楼梯2进入地铁2号线的顺序，采集每个基本单元的行人流运动特性数据。对于乘客有规模流动的区域，乘客运动速度与密度的关系趋势是相似的，如图3所示。

图3 基本单元速度-密度散点

借助Matlab软件的Cftool工具箱对5个基本单元的行人流速度-密度关系进行曲线拟合，拟合函数及其相关系数如表1所示。

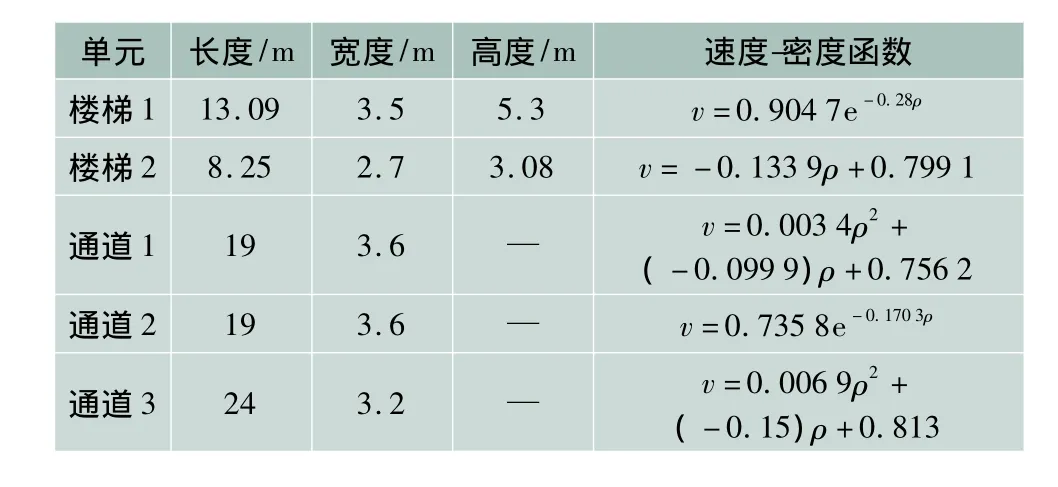
表1 楼梯、通道速度-密度函数

由图3及表1可知，对于行人有规模运动的区域，乘客运动速度随行人流密度的增加而下降，在密度较低(0～1人/m2)时速度下降幅度较小，乘客可自行选择步行速度;随着行人流密度的增加，不同方向行走的乘客间开始受到相互干扰;行人流密度增加到3～5人/m2时，乘客处于聚集状态，行走速度需要不断调整;行人流密度达到5人/m2以上时，乘客处于拥挤状态，行走速度很低，不能超越旁人。

3.2 进站线路疏散能力瓶颈点分析

将进站线路上的各疏散设施(通道、楼梯)简化成节点，并相互连接形成一个排队系统。对于通道1，给定初始的到达率λ，利用GEM算法计算其拥堵概率、吞吐量、通过时间和排队长度等数据，并将通道1的吞吐量作为下一单元(通道2)的到达率，这样依次计算出剩余基本单元的行人流相关数据;同时，通过改变到达率λ，观察不同到达率情况下各个基本单元的拥堵变化状况，并根据各个基本单元的拥堵概率找出西直门地铁站疏散设施的拥堵瓶颈点。

经过实地调研可以发现，通过通道1的行人流，一部分进入4号线站台，其余进入通道2，同时由4号线换乘到2号线的乘客也将有一部分进入通道2。分析行人流数据，可以得到由通道1进入4号线站台的行人流约为0.3人/m2，由4号线进入通道2的行人流约为0.5 人/m2，则通道2 的到达率为 λ(t2)=θ(t1)－0.2+0.5。同理，通过楼梯1的行人流与由西南口进入地铁站的行人流，合并在一起进入通道3，经由地铁站西南口输入到系统中的行人流约为0.2人/m2，则通道3的到达率为 λ(t3)=θ(l1)+0.2。

综上所述，各基本单元到达率的算式分别为:

设定到达率λ为1～8人/s，得到各个基本单元的拥堵概率如表2所示。

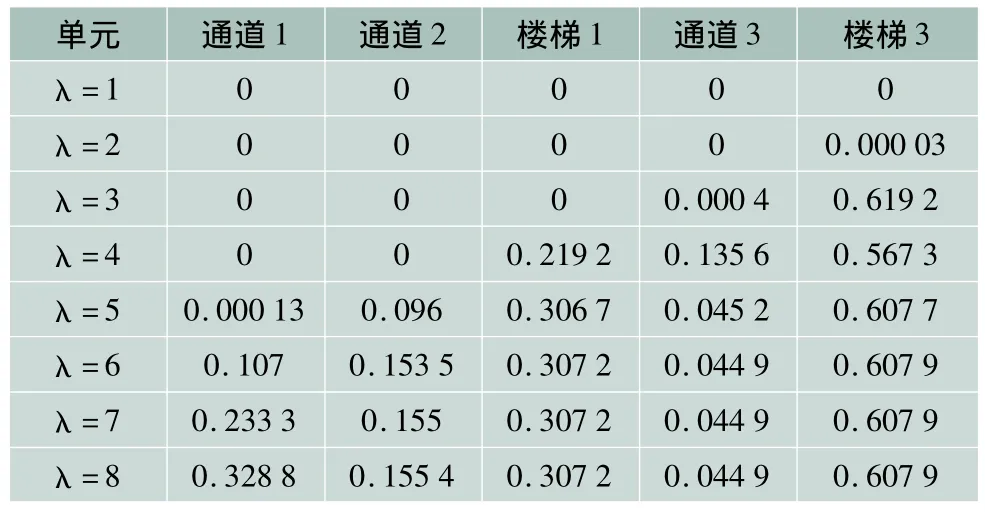
表2 不同到达率情况下各基本单元的拥堵概率

将表2中各基本单元在不同到达率下的拥堵概率以折线图表示，横轴表示拥堵概率，纵轴用序号1～5依次代表通道1、通道2、楼梯1、通道3和楼梯2等基本单元，则不同到达率下的拥堵概率折线如图4所示。

图4 基本单元拥堵概率对比分析

从图4可以看出，楼梯1和楼梯2处拥堵概率较大，即进站路线的拥堵瓶颈主要产生在楼梯1与楼梯2处。此外，基本单元的拥堵概率也会随到达率的不同发生相应的变化。当到达率λ＜2人/s时，进站路线通畅无阻，各通道楼梯拥堵概率P(c)基本为0;当λ=3人/s时，进入站台的楼梯2开始发生拥堵，拥堵概率为0.6左右;当λ≥5人/s时，楼梯1也发生了一定的拥堵，拥堵概率为0.3左右。

3.3 进站线路疏散优化方案

针对上文中分析得出的疏散能力瓶颈点，拟定了以下2套疏解方案。

1)适当增加楼梯2的宽度。从GEM算法计算拥堵概率的公式中可以看出，拥堵概率P(c)与基本单元的宽度w及速度va成正比，与速度vb和v1成反比。其中va、vb和v1是行人流运动特性，无法直接进行控制和改变，因此可以调整楼梯的物理宽度以降低拥堵概率。

由图2可知，楼梯2是进入2号线站台的下行楼梯，其宽度要受到站台宽度的限制，假设站台宽度为wt，楼梯外站台两侧须保证一定的安全距离，设为ws，其他占用宽度设为wp，则楼梯2的宽度w的限制条件为:w≤wt－2ws－wp。由西直门交通枢纽的测量数据可知，2号线站台宽度wt=12 m，安全距离须保证wn=1.5 m，相关设施须预留宽度wp=4 m，这样楼梯2宽度w≤5 m。在此限制条件下，改变楼梯2的宽度，研究其在不同到达率情况下的拥堵概率，如表3所示。

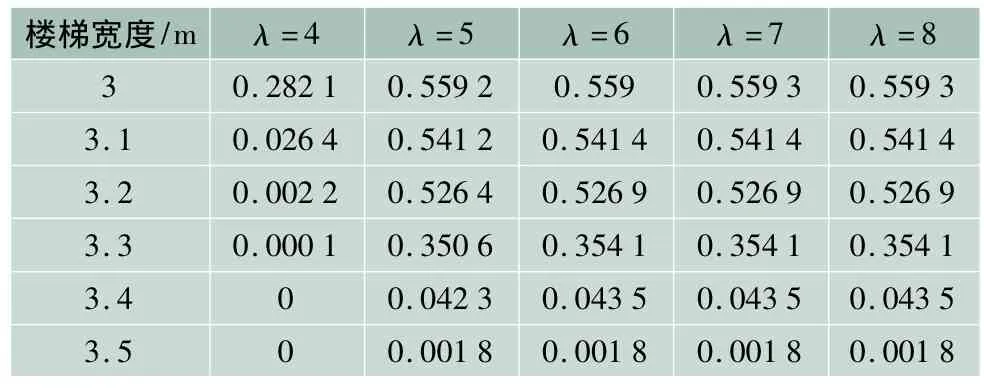
表3 楼梯2不同宽度下的拥堵概率

由表3可以看出:当λ≥5人/s时，楼梯宽度须到达3.4 m才可将拥堵概率降低到0.04左右。因此，为保留一定的通过能力，建议将楼梯2的宽度由2.7 m拓宽到3.4 m，这样可在一定程度上缓解拥堵现象。

2)将楼梯1更换为自动扶梯。对比调研得到的基本单元物理数据，楼梯1的高度相对较高，行人在楼梯上的行走速度较慢，且由于体力的消耗导致行人通过楼梯1后的运动速度会有一定下降。因此考虑将楼梯1更换为自动扶梯，以提供较大的通过能力，并且确保行人可以较高的速度通过之后的通道3，加快乘客的流动。

根据 GB 50157—2003《地铁设计规范》［9］，单向自动扶梯通过能力为9 600人/h，设计速度为0.65 m/s，而对楼梯1来说，其到达率在高峰时期为3～4人/s，但高峰时间一般持续45 min，且到达率会有一定波动，自动扶梯能力可基本满足其需求;且扶梯设计速度高于行人在楼梯上行走的速度，可快速运送乘客。

4 结论

为提高地铁站疏散能力，在分析地铁站行人流运动特性的基础上，构建乘客排队模型，并利用GEM算法进行求解，根据得到的节点拥堵概率、吞吐量等指标，定量分析地铁站疏散能力的瓶颈点，并结合西直门地铁站的空间布局，提出了合理的进站线路疏散优化方案。

将GEM算法应用于解决M/G/c/c排队问题，对于解决地铁车站拥堵和人员的疏散问题进行了比较有建设性的探索。然而由于时间和精力有限，没有针对全站进、出站线路进行统一的建模和分析。另外，在计算线路疏散能力瓶颈点时没有考虑收费闸机等设施对通过能力的影响，有待进一步的研究。

［1］陈绍宽，刘爽，肖雄，等.基于M/G/c/c模型的地铁车站楼梯通道疏散能力瓶颈分析［J］.铁道学报，2012，34(1):7-12.

［2］Cheah J，MacGregor S J.Generalized M/G/C/C state dependent queueing models and pedestrian traffic flows［J］.Queueing Systems，1994(15):365-386.

［3］MacGregor S J.Application of state-dependent queues to pedestrian/vehicular network design ［J］.Operations Research，1994，42(3):414-427.

［4］Cruz F R B，MacGregor S J.Approximate analysis of M/G/c/c state-dependent queueing networks［J］.Computers ＆Operations Research，2007(34):2332-2344.

［5］方正，卢兆明.试论建筑物人员疏散的量化研究［J］.武汉大学学报:工学版，2002，5(2):71-74.

［6］宋卫国，于彦飞，陈涛.出口条件对人员疏散的影响及其分析［J］.火灾科学，2003，12(2):100-104.

［7］柳伍生，余朝玮.地铁站楼梯行人流交通特征的数据拟合分析［J］.计算机工程与应用，2008，44(3):50-52.

［8］Cruz F R B，MacGregor S J，Medeiros R O.An M/G/C/C State-dependent network simulation model［J］.Computers ＆Operations Research，2005(32):919-941.

［9］GB 50158—2003地铁设计规范［S］.北京:中国计划出版社，2003.

Capability of Passenger Evacuation of Metro Station Based on GEM Algorithm

Xu Wenchao Zhou Leishan
(School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044)

Abstract:For analyzing and improving the evacuation ability of metro station facilities and ensuring the passengers' safety, GEM(Generalized Expansion Method) algorithmfor passenger evacuation was adopted to establish the model of passenger evacuation based on analyzing the characteristics of passenger movement.Congestion probability and handling capacity of the evacuation facilities of the station were calculated; evacuation bottlenecks to the metro station were found out. Case study of Xizhimen Station was carried out to verify the feasibility of GEM algorithm to determine the evacuation capability of a metro station with the evacuation optimization scheme proposed with feasible approaching lines to the station.

Key words:metro station; passengers; capability of evacuation;GEM algorithm

U231.92

A

1672-6073(2013)01-0024-05

10.3969/j.issn.1672-6073.2013.01.007

收稿日期:2012-04-12

2012-12-04

作者简介:许文超，女，硕士研究生，从事交通运输规划与管理的研究，11121016@bjtu.edu.cn

周磊山，男，教授，博士生导师

国家科技支撑计划重点项目(2009BAG12A10)

(编辑:曹雪明)