知识驱动的三角网格模型分割

贺 强，张树生，白晓亮

(西北工业大学 现代设计与集成制造技术教育部重点实验室，710072 西安)

逆向工程是根据已有实物或模型重建计算机辅助设计(computer aided design，CAD)模型的过程.基于特征的逆向工程技术是产品创新设计的有效手段，分割是其中的关键技术之一［1］.国内外学者提出了多种分割算法，如区域生长［2－4］、分水岭［5－7］、聚类［8－9］、特征线提取［10－11］等.区域生长方法通过选取不同类型的种子元素，搜索与种子具有相似性质的点以构成曲面.该类算法的主要缺点是高度依赖初始种子的选取，会产生过分割.分水岭方法计算顶点的曲率或其他高度函数来确定子网格之间的分界线(即分水岭)，然后根据分界线将模型分割为多个子网格.由于噪声，高度函数的估算必然有一定的离散性，因此该方法容易发生过分割.文献［7］通过动态拟合曲面的方式提高了曲率估算的精确性，从而提高了分水岭算法对噪声的鲁棒性.聚类方法将具有相同属性的元素聚类，实现网格分割.文献［8］根据顶点间的测地线距离，利用模糊聚类的方式实现了网格模型的层次分割.文献［9］将平面、球面和圆柱面拟合的最小误差作为聚类准则对模型的三角形进行聚类.这类方法在一定程度上降低了曲率或其他几何属性估算的准确性对分割的影响，但常常丢失曲面间的拓扑关系.特征线提取利用法矢和曲率信息识别出模型中尖锐的边和顶点，连接它们形成分割依据的特征线.这类方法在处理含过渡面的模型时，特征线的完整性差.文献［11］在消除了过渡区域的低分辨率网格上提取特征线，然后将特征线映射到原始模型上，从而得到相对完整的特征线.

综上，当前的分割算法几乎不以高层次的特征为目标，因此分割的结果难以体现意义.本文将模型分割成曲面，进而提取模型所含有的、具备一定工程语义的特征，从而从曲面这一基本造型元素和工程语义的角度来体现分割的意义，为基于特征的逆向工程中的关键步骤——CAD 模型重建中的特征重建和约束施加奠定了基础.

1 知识库的构成

工程领域产品的三角网格模型通常能够分解成基本的曲面元素，如平面、圆柱面、圆锥面和球面等.这些几何元素满足一定拓扑约束关系的有机组合就形成了具有工程语义的、可以更高层次反映设计意图的基本造型体特征和加工特征.知识库作为有意义分割的知识先验，应该能反映该领域具有代表性的几何结构及其工程语义.因此，知识库由包含了长方体、圆柱体、圆台体、孔、台阶、凸块、型腔和槽等特征的以面为节点的属性邻接图表示构成.每个特征的属性邻接图的边的属性对应为特征的面与面之间的平行、垂直和相交的凹凸性等关系.知识库可以根据需要进行种类的扩充.

2 基于二次曲面拟合误差和曲率的曲面分割

二次曲面频繁出现在工程产品的外形上，甚至很多产品外形完全由平面、圆柱面、圆锥面和球面组成［12］.因此，逆向工程中，以这几类曲面的拟合误差作为分割的准则能体现分割的意义.此外，对复杂模型，提取简单类型的曲面比复杂类型要可靠得多，因此按照曲面类型的几何复杂性指定一个分割次序是很有意义的.除二次曲面外，模型中还存在自由曲面，对其分割则需采用基于曲率的方法，本文改进了噪声鲁棒的法向量投票方法［13］来计算曲率.本文曲面分割的整体流程如图1 所示.

图1 曲面分割流程

2.1 误差和曲率的计算

曲面拟合误差和曲率的计算必须准确且高效才能满足网格分割效果和时间效率的要求.本文采用如下方式计算曲面的拟合误差和曲率.

平面待拟合点集的协方差矩阵为

式中:wi是顶点vi一阶邻接三角形的面积和.n 是拟合点的数量.矩阵Mc的三个特征值中最小的一个对应的特征向量即为拟合平面的法向，拟合误差计算如下

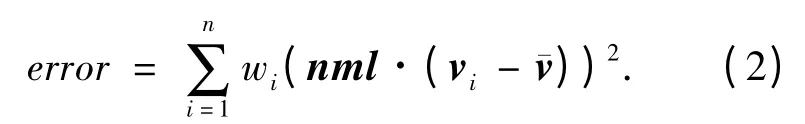
球面 球面由球心(x0，y0，z0)和半径r 确定，将球面方程转化为如式(3)所示的向量表示，采用线性最小二乘法即可求出球心、半径.

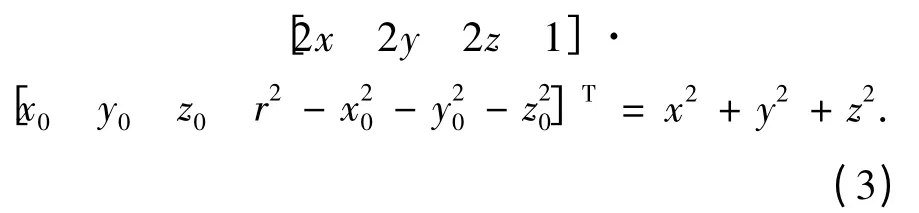
则拟合误差为

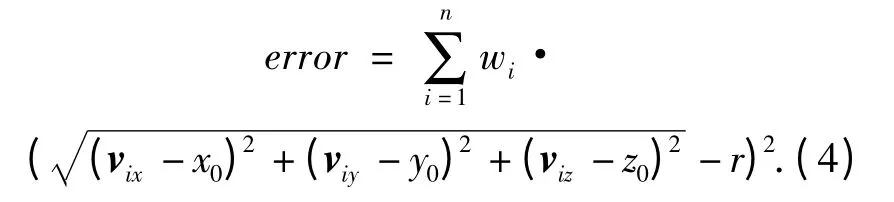
圆柱面圆柱面由其轴线上任意一点o，轴线的单位矢量n，横截面圆的半径r 确定.圆柱面上任意点的法向量都与n 垂直.因此，圆柱面上任意一点的法向量都在过原点，法向为n 的平面上.首先对拟合点的法向量采用上述拟合平面的方式求出圆柱面的轴线方向n.以拟合平面过程的协方差矩阵的三个特征值对应的特征向量建立坐标系，将点投影到该坐标系下.在二维空间中，以圆方程拟合投影点集，得到圆心和半径.将圆心变换到原始坐标系下即为o，则圆柱面的拟合误差为

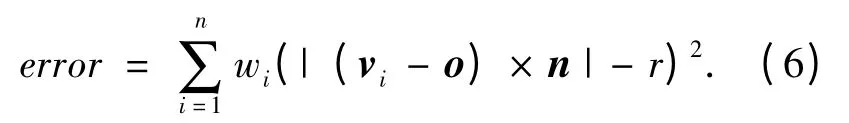
圆锥面圆锥面由锥顶点p，轴线方向n，圆锥角的一半a 确定.圆锥面上任意一点的法矢与n的夹角为π/2－a，因此圆锥面上点的法向量构成平面(n，－sin a).首先拟合顶点的法矢量求得圆锥的轴线方向和圆锥的锥顶角.然后将获得的参数带入圆锥面方程，通过线性最小二乘拟合剩余的待求参数，则圆锥面的拟合误差为

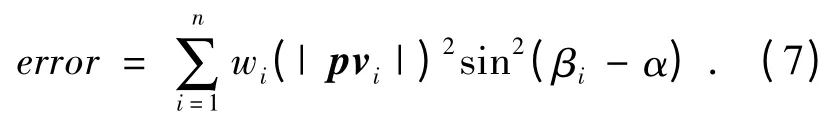
式中:βi是pvi与n 的夹角.

曲率 顶点v 的二阶邻接三角形集合为Mv，由如图2 所示的标号为1，2 的三角形组成.集合中的三角形Fi的重心为ci，法矢为Nfi，面积为Ai.它在v 上的“投票”Ni定义为

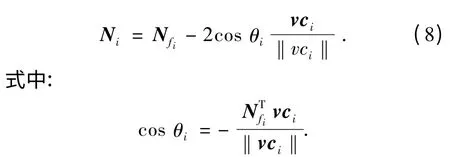
对Mv中每一个三角形计算其对v 的投票，则Mv的投票效应矩阵为

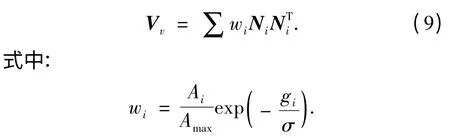
其中，Amax是模型中三角形面积的最大值.σ=gm/3，gm是模型网格边的平均边长，gi是ci到v 的测地距离.由于测地距离计算非常耗时，因此本文采用如图2 所示的方式来近似计算.对标号为1 的三角形直接利用其重心到顶点v 的欧式距离近似，对标号为2 的三角形，若是与一阶三角形共边，则用重心到边的欧式距离与顶点v 到垂足的欧式距离之和近似;若是与一阶三角形共顶点，则用重心到该顶点的距离与顶点v 到该顶点距离之和近似.投票效应矩阵为3×3 的对称矩阵，特征值为λ0≤λ1≤λ2，两个主曲率为:k1=3λ1－λ2，k2=3λ2－λ1.

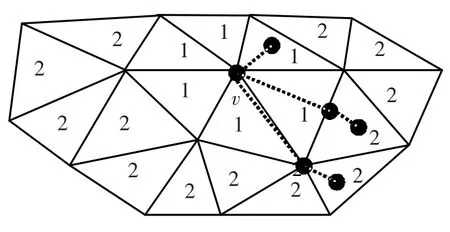
图2 顶点v 的二阶邻接三角形集合

2.2 初步的分割方法

设M(V，E，T)是三维空间中的二维流形的三角网格模型.V 是模型顶点的集合，E 是连接顶点的边的集合，T 是模型中的三角面片的集合.M对应的图G(C，A)定义如下:图节点集合C 中每一个节点对应T 中的一个三角面片，M 中两个相邻的三角面片对应的图节点构成的边形成图边集合A，如图3a 所示，虚线网络即为网格模型对应的图结构.建立了模型对应的图后，利用上述曲面拟合误差和曲率的计算方法来计算图边的权值.图边的权为该边两个节点对应三角形拟合某种曲面的误差或曲率差.具体的分割流程如下:

首先以平面的拟合误差作为图中边的权值，分割出模型中所包含的平面，然后分别以球面、圆柱面和圆锥面的拟合误差作为权值进行对应曲面类型的网格分割，对图中已经确定了曲面类型的节点，不再分割.最后对剩余的节点，计算其对应的网格顶点的曲率，图边的权值更新为对应节点所包含三角形顶点的曲率差.本文的曲率差定义为顶点平均曲率的差的绝对值.分割的结果统一标记为“其他”.每类曲面的分割流程如下:

Step 1 根据边的权值为所有图边构建一个小顶堆，并设置边折叠的阈值ε1和对应曲面分割完成的阈值ε2.首先获取堆顶的边，以该边的任意一个节点作为种子节点，如图3(b).

Step 2 折叠与种子节点直接连接的且边的权值在ε1之内的所有边，生成一个新的图节点，并更新邻接关系和边的权值，如图3(c)，删除小顶堆中所有已经折叠的边.

Step 3 以新生成的图节点作为种子节点，进行Step2 的处理，直至所有与种子节点直接连接的边的权值均大于阈值ε1，则该节点对应的三角形集合构成一个曲面，对该节点进行相应的曲面信息的标记，如图3(d).

Step 4 从小顶堆中取出堆顶的边，以该边的任意一个节点作为种子节点.转至步骤Step 2，Step 3 直至堆顶的边的权值大于ε2.

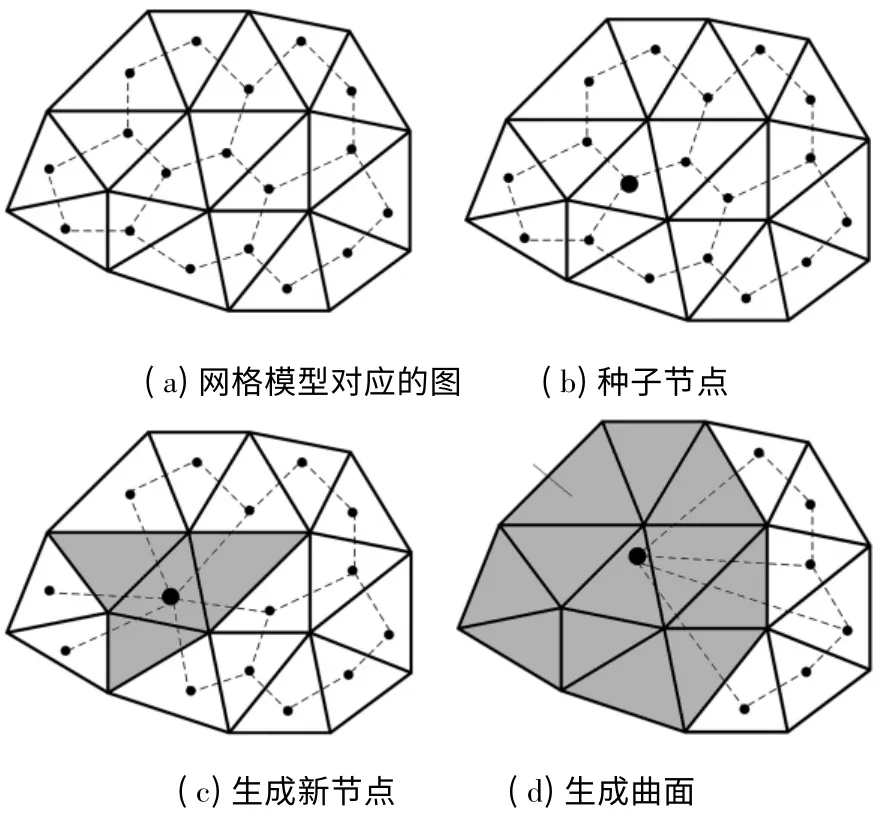
图3 网格模型对应的图及其分割示意

完成曲面分割后，会形成如图4 所示的聚类图.

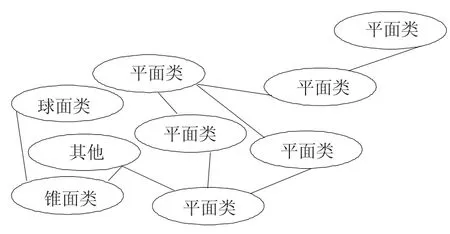
图4 曲面分割结果的示意

图4 中的边表示对应曲面类型的两个子网格拥有相同的边界.因此曲面分割的结果不仅确定了各个子网格对应的曲面类型，还获得了曲面间的拓扑连接关系，为后续的特征分割打下了坚实的基础.

3 基于知识的特征分割

根据初步分割的结果，为模型建立以面为节点的属性邻接图(此处称为大图).以知识库中的属性邻接图作为输入子图，这样从工程语义角度体现分割意义的问题被转换为在大图中寻找同构子图的问题.匹配出大图中与知识库中同构的子图所对应的子网格模型并赋予相应的语义信息就完成了特征分割.

属性邻接图的构建:通过上述初步分割过程，网格模型被分解成平面、球面、圆柱面、圆锥面等曲面的集合(包括曲面的参数信息和邻接关系).根据这些信息，可将模型转化成一种属性邻接图.在该属性邻接图中，每一个图节点对应模型曲面集合中的一个曲面，曲面面的几何属性(类型、几何参数)作为节点的属性;节点与节点之间的关系对应模型中面与面之间的关系，常见的关系包括相邻、邻边的凹凸性、平行、垂直、同轴和共面等.具体构建步骤如下:

Step 1 遍历组成网格模型的曲面集合中的每一个面，同时对应地创建一个属性邻接图节点，将面的几何属性作为对应属性邻接图节点的属性.

Step 2 对集合中的每两个面，利用初步分割得到的聚类图中的图节点之间的邻接关系和面的几何参数计算出两者之间的关系，作为其对应的属性邻接图的节点之间的关系.

局部匹配算法:在模型的属性邻接图中搜索与知识库中的图同构的子图被证明是一个NP 完全问题［14］.NP 完全问题，即完全多项式复杂程度的非确定性问题，是不存在多项式时间算法问题的一个子类，它的特征是如果它们中的一个是多项式可解的话，那么所有其他问题也是多项式可解的.该类问题求解的时间复杂度较高.文献［14］的方法被认为能够代表子图同构问题当前的技术发展水平.该算法的关键在于增量地建立连接图并使用方便的剪除规则和设计了低内存消耗的数据结构.本文在此基础上，充分利用了模型的自身特征，如考虑模型面的类型极其邻接关系等，来使得模型属性邻接图中所含有的、与知识库中的图同构的子图能够较快地匹配.具体过程如下:

设知识库中的某个特征的属性邻接图g(V，E)的邻接矩阵为MB×B，模型曲面分割构成的属性邻接图G1(V1，E1)的邻接矩阵为MI×I.图g 的节点集合V 中的节点数量为B;图G1的节点集合V1中的节点数量为I;E，E1分别为两个图的边的集合.设置一个映射矩阵MB×I，其中任意一个元素mij(0 ≤i ≤B－1，0 ≤j ≤I－1).若图g 的第i 个节点与图G1中的第j 个节点属性相同且与两个节点直接连接的边的数量一致，则mij=1;否则mij=0.图g 与图G1子图同构就是存在这样一个映射矩阵，其每一行有且只有一个1，每一列至多只有一个1.

映射矩阵MB×I设置完成后，开始子图同构匹配搜索.定义两个集合V2，V3分别用于存储搜索过程中2 个图上已匹配的节点，初始时都置为空.从MB×I的第一行开始，从左到右查找值为1 的列.对第i 行，若其第j 列的值为1，并且该列未被占用，则表示找到一个可能匹配的顶点对:图g 的第i 个节点和图G1的第j 个节点对应，将这两个节点分别加入到V2，V3中.如果新加入的2 个节点在最终的同构映射中确实是对应匹配的节点对，则当前图g 中已匹配上的节点集合V2与图G1中已匹配上的节点集合V3构成的子图必定也是同构的.根据这一原理，通过测试V2构成的子图与V3构成的子图是否同构来判断新找到的列是否有效;如果两个集合构成的图子图同构，则该新找到的列是有效的，设置占用标志，进入下一行;反之，在当前行继续搜索下一个有效列;如果当前行搜索完成都没有找到一个有效列，则退回上一行，并且从上一行已经占用列的下一列开始搜索.

4 实验结果

在VS2008 的环境下，利用C++语言实现了算法，在主频1.8 G，内存1 G 的PC 机上运行程序.从分割成曲面、分割成特征和算法时间效率三个方面来验证本文提算法的有效性.

4.1 分割成曲面

为了验证本文曲面分割的效果，将本文初步分割的结果与文献［9］进行对比.图5(a)为待分割的三角网格模型，图5b 为文献［9］在聚类数目为18 下的分割结果(每一种颜色对应一个聚类).图5(c)为本文的曲面分割的结果(对应各个曲面类型的子网格单独显示).图6 为含有自由曲面类型的模型的分割.图6(b)为文献［9］聚类数目为9 的分割结果.图5 的结果表明，以平面、圆柱面、球面的拟合误差为曲面分割准则，本文的初步分割能取得与文献［9］相当的效果.本文曲面分割的各个子网格精确对应相应的曲面，也证明了本文曲面拟合误差计算的精确性满足分割的要求.图6 结果表明，文献［9］由于缺少对自由曲面的处理，因此不能有效分割出自由曲面类型的网格，而本文的算法则增加了这一能力.此外，文献［9］的方法不能得到曲面间的邻接关系和曲面类型信息，因此不能获得更高层次的分割结果.

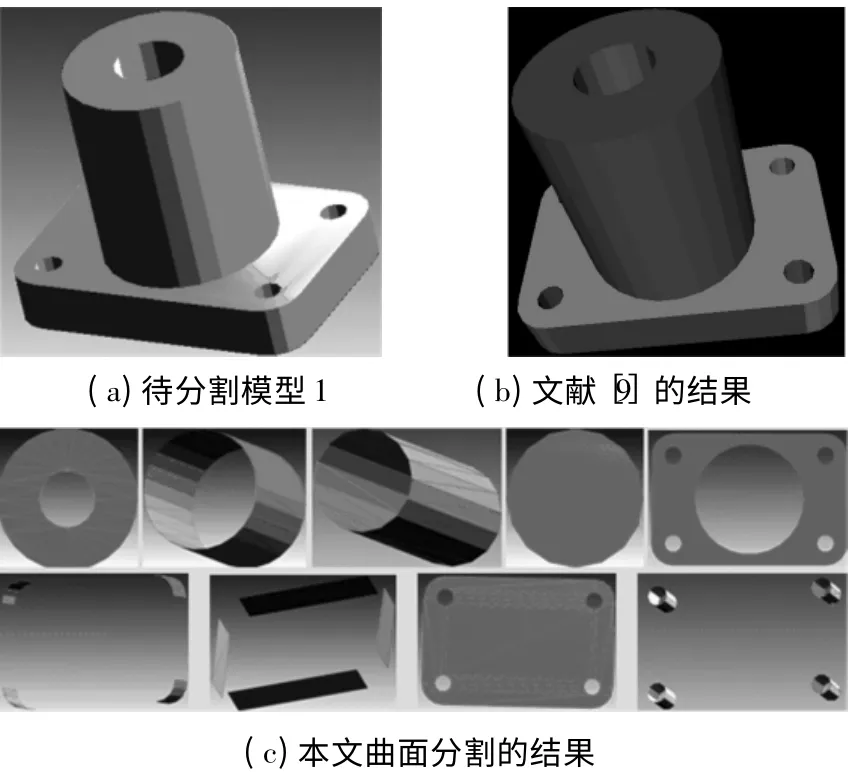
图5 模型1 的分割与比较

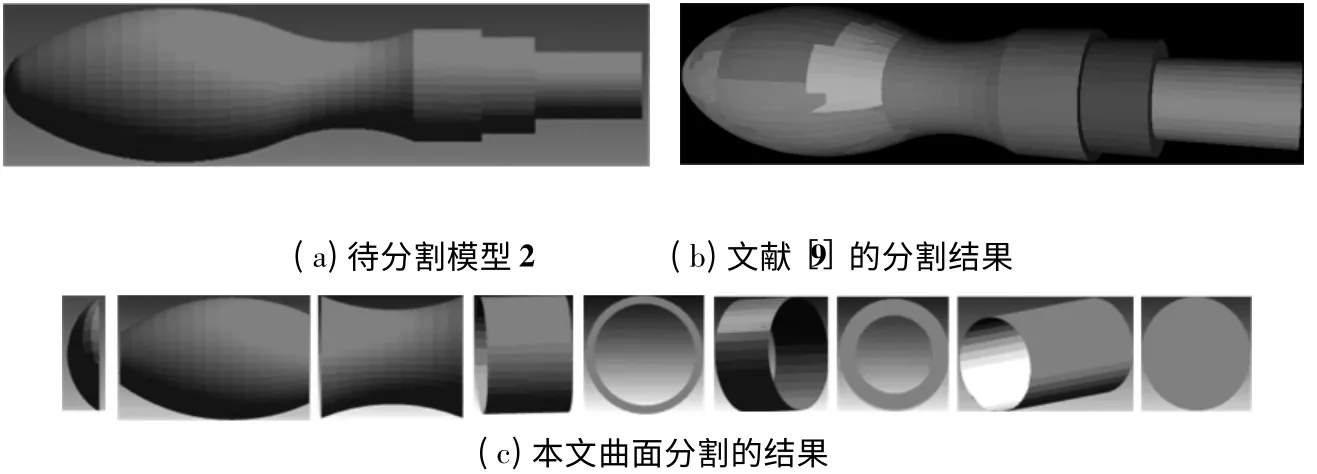
图6 模型2 的分割与比较

4.2 分割成特征

根据本文初步分割得到的曲面集合及其相互之间的邻接关系，以知识库中的属性邻接图作为输入，匹配出模型中对应知识库中的特征的子网格.图7 为模型1 根据知识库分割得到对应特征的网格部件.实验结果表明，分割的结果能显著地体现工程语义，为逆向工程的特征重建打下了坚实的基础.

4.3 分割执行时间

文献［9］的算法具有极高的时间效率.本文虽然增加了一类曲面的拟合误差和曲率的计算，但采用了逐次分割的策略，每次只需要计算一种曲面的拟合误差并只对部分顶点计算曲率，因而时间效率也较高.表1 为本文初步分割的计算时间与文献［9］的比较以及本文对模型1 分割出对应特征类型的子网格时，图同构匹配的时间.

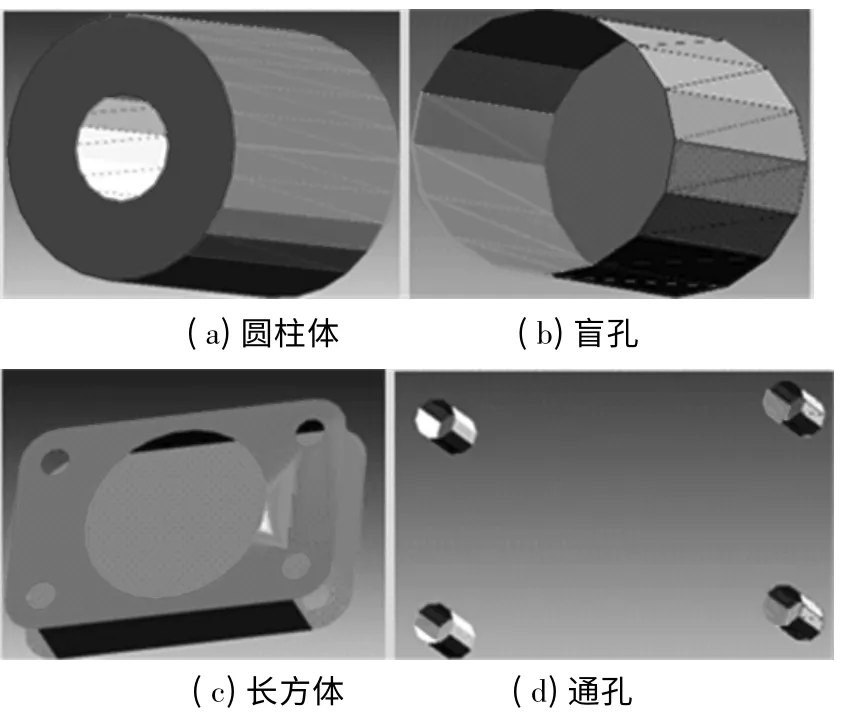
图7 模型1 的体现工程语义的特征分割

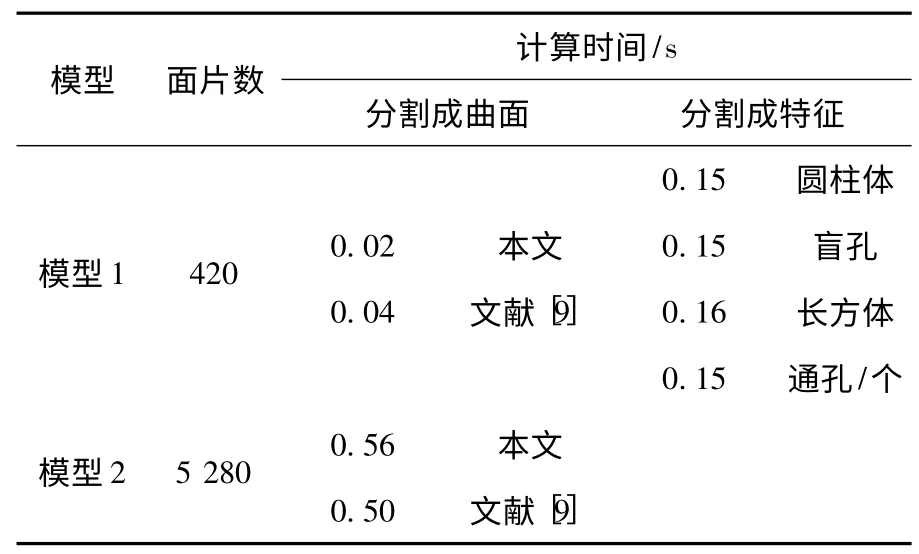
表1 曲面分割和图匹配的执行时间

5 结论

本文针对机械领域的三角网格模型，设计了一种快速的、能从曲面和工程语义两个角度体现分割意义的分割算法.建立了指导网格有意义分割的先验知识库;逐次地分割出模型中的平面、球面、圆柱面、圆锥面，并利用曲率将剩余的模型分割成曲面，同时获得了曲面的类型信息和拓扑连接关系;利用知识库的特征的属性邻接图匹配出具有工程语义的网格部件从而完成了网格模型有意义的分割.实验证明，对不含复杂自由曲面的模型，本文在曲面这一基本造型元素和工程语义两个层次上取得了有意义的分割结果，为基于特征的CAD 模型重建奠定了基础.本文主要从加工特征和基本造型特征方面体现工程语义，然而从模型重用的角度而言，机械领域中常见的典型结构的重用粒度更高，因此，如何从模型重用的角度来体现分割的意义是一个有意义的研究方向.

［1］Ye Xiuzi，Liu Hongzheng，Chen Lei，et al.Reverse innovative design—an integrated product design methodology［J］.Computer-Aided Design，2008，40(7):812－827.

［2］LAVOUE G，DUPONT F，BASKURT A.A new CAD mesh segmentation method based on curvature ［J］.Computer-Aided Design，2005，37(1):975－987.

［3］ZUCKERBERGER E，TAL A，SHLAFMAN S.Polyhedral surface decomposition with applications［J］.Computers＆ Graphics，2002，26 (5):733－743.

［4］GUILLAUME L，FLORENT D，ATILLA B.Constant curvature region decomposition of 3D meshes by a mixed approach vertex-triangle［J］.Journal of WSCG，2004，12 (1):245－252.

［5］PAGE D L，KOSCHAN A F，ABIDI M A.Perceptionbased 3D triangle mesh segmentation using fast marching watersheds［C］//Proceeding of Computer Vision and Pattern Recognition.Madison，Washington DC，USA:IEEE，2003:27－32.

［6］ZHOU Yinan，HUANG Zhiyong.Decomposing polygon meshes by means of critical points［C］//Proceedings of the 10thInternational Multimedia Modeling.Washington DC，USA:IEEE，2004:187－196.

［7］钱江，陈志扬，叶修梓，等.噪声鲁棒的分水岭网格分割算法［J］.计算机辅助设计与图形学学报，2008，20 (3):310－315.

［8］KATZ S，TAL A.Hierarchical mesh decomposition using fuzzy clustering and cuts［J］.ACM Transactions on Graphics，2003，22(3):954－961.

［9］ATTENE M，FALCIDIENO B，SPAGNUOLO M.Hierarchical mesh segmentation based on fitting primitives［J］.The Visual Computer，2006，22 (3):181－193.

［10］LEE Y，LEE S，SHAMIR A，et al.Mesh Scissoring with Minima Rule and Part Salience［J］.Computer－Aided Geometric Design，2005，22(5):444－465.

［11］白晓亮，张树生.多分辨率三角网格基础上的区域分割［J］.中国机械工程，2009，20(9):1097－1101.

［12］VANCO M，HAMANN B，BRUNNETT G.Surface reconstruction from unorganized point data with quadrics［J］.Computer Graphic Forum，2008，27(6):1593－1606.

［13］PAGE D L，SUN Y，PAIK J，et al.Normal vector voting:crease detection and curvature estimation on large，noise meshes［J］.Graphical Models，2002，64(1):199－229.

［14］CORDELLA L，FOGGIA P，SANSONE C，et al.Performance evaluation of the VF graph matching algorithm［C］//Proceedings of the 10th international conference on image analysis and processing.Washington DC，USA:IEEE，1999:1172－1177.