薄壁箱型结构仿真与实验稳定性分析*
2013-09-16陈玉振陈亚峰
陈玉振,陈亚峰
(南京电子技术研究所, 江苏 南京 210039)
薄壁箱型结构仿真与实验稳定性分析*
陈玉振,陈亚峰
(南京电子技术研究所, 江苏 南京 210039)
文中以单节薄壁箱型结构为研究对象,针对不加筋和加筋2种结构形式,利用ANSYS特征值屈曲分析和实物试验对其进行稳定性研究,得到了加筋前后薄壁结构的极限失稳载荷和屈曲形态。仿真与试验结果都表明,加强筋的设置显著提高了薄壁箱型结构的极限失稳载荷,是一种非常有效的提高薄壁结构稳定性的方法。特征值屈曲分析得到的屈曲形态与试验比较一致,可方便快速地为加强筋的形状和位置优化提供理论依据。
屈曲分析;稳定性;有限元;薄壁箱型结构
引 言
现代工程结构的设计,经常会采用由高强度合金制成的细长杆件和薄壁板壳等结构型式。对于此类结构,其破坏往往不是由于结构材料达到了强度极限,而是由于发生了屈曲失稳。这种屈曲失稳可能是弹性的,也可能是非弹性的,可能是局部性的,也可能是全局性的。局部性失稳在引起弹性压屈的载荷作用下并不发生破坏,相反,其抗力随着压屈的进展而不断增大;全局性失稳会使结构在无任何征兆的情况下完全失去承载能力,发生灾难性破坏,造成严重的后果。因此,为保障薄壁壳体结构的安全性,不仅要校核其强度和刚度状态,还必须考虑其失稳破坏应力,即进行屈曲稳定分析,确定结构开始变得不稳定时的临界载荷和屈曲模态形状[1-2]。
某型雷达升降塔塔身采用了将薄壁钢板折弯后焊接成方管的加工方法。在塔身一侧承受较大风载荷的情况下,由于弯矩作用,背风面处于受压状态。取塔身其中一节进行失稳计算, 并为试验提供加载和初始缺陷参考,为塔身整体稳定性设计改进提供依据[3]。
1 有限元仿真计算
近年来由于计算机的迅速发展,在关于壳体问题的数值解法方面,有限单元法得到了日益发展和应用,特别是对解决复杂结构的失稳问题很有成效。本文利用ANSYS有限元通用软件对薄壁方管构件进行了特征值(线性)屈曲分析,得到了一阶屈曲模态和结构临界失稳载荷。
1.1 基本理论
有限元法中屈曲问题的平衡方程为
(t[K]0+t[K]σ+t[K]L+t[K]g)×{Δq}=
[K]T×{Δq}={ΔΨ}
(1)
式中:t[K]0为通常意义的刚度矩阵;t[K]σ为初应力刚度矩阵;t[K]L为初位移或大位移矩阵;t[K]g为初载荷刚度矩阵;Ψ表示内力和外力的向量和;q表示位移。
根据虚位移原理,对平衡状态有:
dП=d{q}T{Ψ}=0
(2)
则有:
d2П=d{q}T[K]Td{q}=0
(3)
若П的二阶变分是正值,则平衡是稳定的;反之,若是负值,则平衡是不稳定的。这就是大变形下结构稳定性的判断依据。
1.2 建立有限元模型
对实体模型进行取中面建模,利用壳单元进行网格划分,截面尺寸为364mm× 364mm,为使结果尽可能精确,采用扫略网格划分,单元尺寸选为10mm。材料为高强钢,弹性模量为2.068e5MPa,泊松比为0.3,屈服强度为700MPa。加载方式为底部固定,顶部定义加载质量点来施加水平集中力。其几何模型及有限元模型如图1所示。
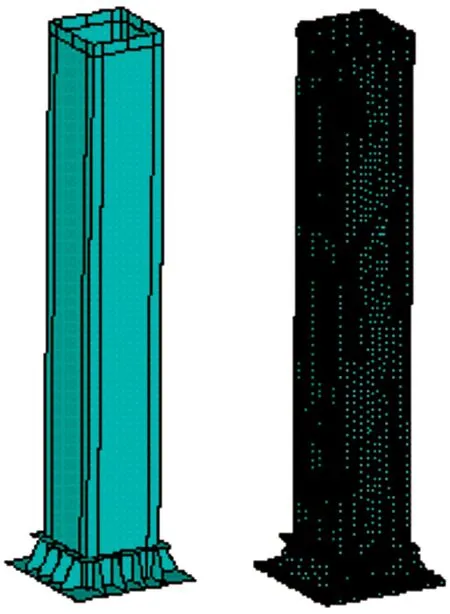
图1 几何模型及有限元模型
1.3 屈曲计算[4]
对方管进行特征值(线性)屈曲计算,得到局部失稳时的一阶屈曲模态,如图2所示。屈曲发生在方管受压侧一面的根部,为一列纵波。施加载荷为1t,计算得到屈曲载荷因子为1.6,所以结构的失稳临界载荷为1.6t,远小于强度破坏载荷7.1t,可见结构在强度破坏之前已发生屈曲失稳。从图2可以看出,受压侧钢板在压应力方向上皱损成3个半波,在垂直方向仅有1个半波,这与板的屈曲理论规律一致。

图2 不加筋试件局部屈曲形态图
为提高结构的稳定性,在筒内壁四周焊装冲压成形的加强筋,如图3所示。

图3 加筋示意图
对加筋后的方管进行特征值屈曲计算,在顶部施加的集中力为1t,得到的屈曲因子为9.0,所以加筋后结构的临界失稳载荷为9t。加筋后的一阶屈曲模态如图4所示,与不加筋时有所不同,方管根部出现了两列纵波。

图4 加筋试件局部屈曲形态图
2 屈曲试验
如图5所示,方管底端固定,顶部水平施加周期为60s的正弦位移波。加载峰值位移从1mm到60mm,实行逐级加载且每次加载完毕后都卸载到零。根据仿真计算得到根部屈曲波形图,在底部波峰处安装位移计和应变片,并在根部贴应变片以监测最大应力。

图5 模型及试验加载示意图
2.1 未加筋方管加载试验
如图6所示,当水平位移加载到8mm、对应加载力为1.1t时,应变量发生突变,说明薄板已经发生了局部屈曲。数据分析发现,当方管发生局部凸凹变形时,褶皱处的测试应力仅为12MPa,还远未达到其屈服强度700MPa。当加载载荷达到2.6t时,方管在下部的板面出现了明显的屈曲特征;当水平力增大到2.7t时,薄板根部测试应力为691MPa,基本达到了材料的屈服强度极限。
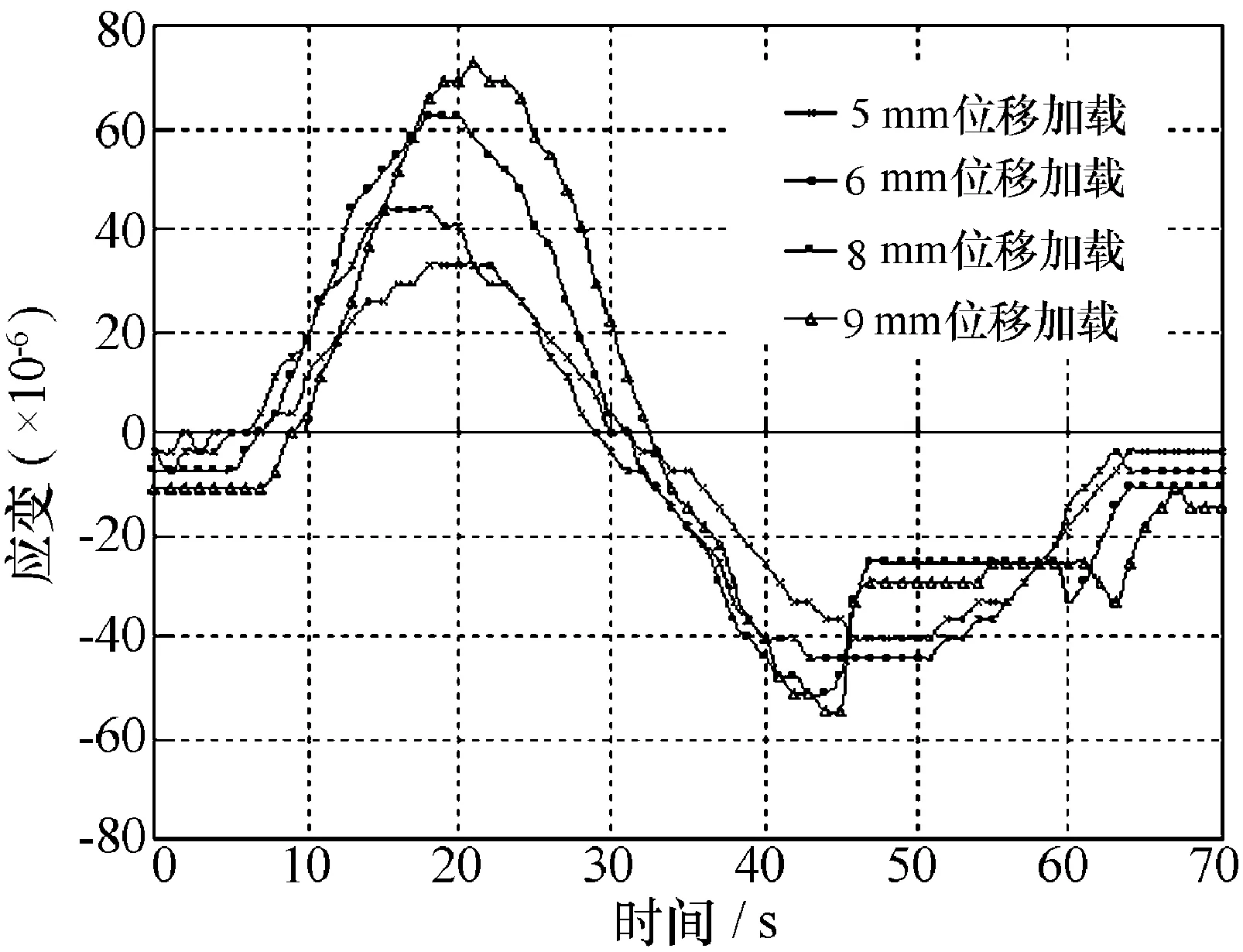
图6 波峰处应变片应变-位移曲线
材料达到屈服极限之后,结构的承载能力仍继续提高。当顶部载荷达到4.6t时,结构完全失去承载能力,发生整体破坏。但从图7可以看出,整体破坏之前结构的力-位移曲线基本上还是线性的,说明局部屈曲并没有明显改变此薄壁结构的承载能力,结构在发生局部屈曲后,不会出现整体垮塌现象。
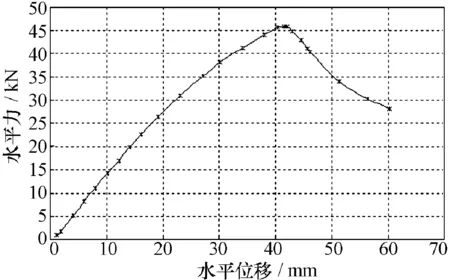
图7 未加筋构件整体承载力-位移曲线
2.2 加筋方管加载试验
采用相同试件,如图3所示在方管内四周焊装加强筋,测试方法如图8所示。

图8 加筋试件位移计及应变片安置图
加筋后,加载直至结构件完全破坏,未出现异常现象,说明在完全强度破坏之前未发生局部失稳。如图9所示,加筋后结构极限破坏载荷为7.6t。
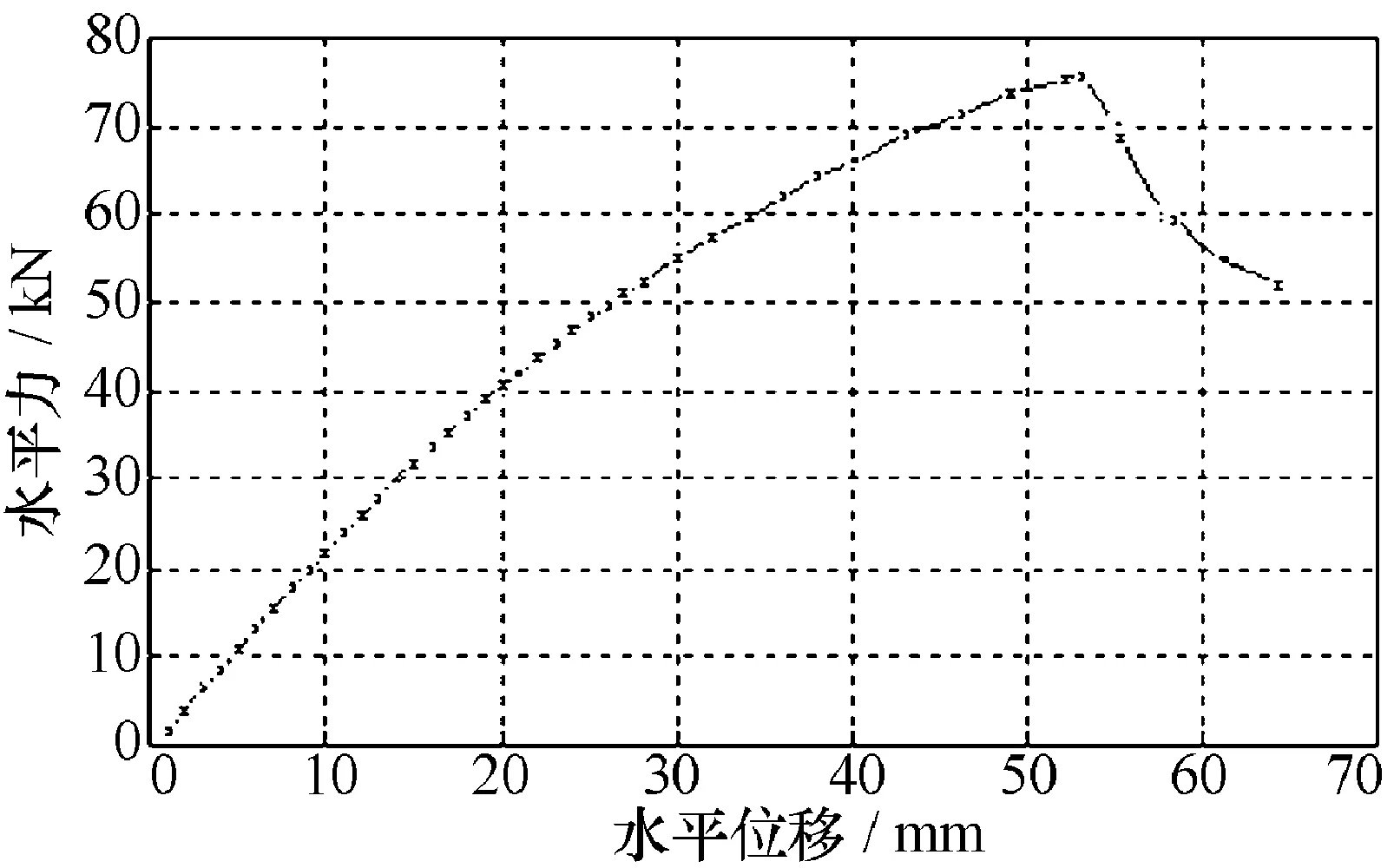
图9 加筋构件整体承载力-位移曲线
仿真与实验结果显示,板的纵向加筋能减小薄板的宽厚比,从而能有效增强板受压时的稳定性,使其屈曲承载力成倍提高。由于试件材料性能的随机性以及试件在加工过程中的残余应力及其他未知缺陷都不能通过现有设备进行度量,因此,理论分析与试验数据分析有一定的差距,实验测得的失稳极限载荷约为有限元计算结果的70%。
3 结束语
从仿真和试验结果可以看出,薄壁方管结构在受侧向力作用时,受压侧一面的根部易发生局部屈曲失稳。但失稳后结构的承载能力并没有受到显著影响,仍能继续承载,并且极限承载能力大大高于临界失稳载荷。
加筋对提高薄壁方管构件的稳定性和极限承载能力都有非常显著的效果,特别是加筋后的临界失稳载荷提高了数倍之多。所以在受结构重量限制不能过多增加壁厚时,加筋是一种简单有效的方法。
在稳定性问题的计算方面,有限元仿真准确地预测了结构的屈曲形态,与试验现象相符。由于模型加工过程中几何缺陷和材料缺陷等因素的影响,仿真计算得到的临界失稳载荷约为试验结果的70%,结构设计时可通过适当提高安全系数予以补偿。
特征值屈曲计算得到的临界失稳载荷与试验研究相比,仿真计算成本低,效率高,在产品设计周期较短的情况下,其易于修改的特点为技术人员进行结构优化设计提供了可靠的理论依据。
[1]YOUNGWC,布迪纳斯. 罗氏应力应变公式手册[M]. 岳珠峰, 高行山,译. 北京:科学出版社,2005.
[2] 彭云, 易龙, 南英.复合材料盒段结构屈曲稳定性分析及优化技术[J]. 航空计算技术,2006,36(5):80-82.
[3] 程林.复合材料桅杆稳定性分析[J].电子机械工程,2010,26(1):47-49.
[4] 刘相新, 孟宪颐.ANSYS基础与应用教程[M].北京:科学出版社,2006.
陈玉振(1982-),男,工程师,硕士,主要从事雷达机械传动设计仿真工作。
陈亚峰(1975-),男,工程师,硕士,主要从事雷达机械传动设计仿真工作。
Stability Analysis of Thin-walled Box by Simulation and Test
CHEN Yu-zhen,CHEN Ya-feng
(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
In this paper the instability ultimate load and the first order modal are obtained against box structures with reinforcement and non-reinforcement by ANSYS eigenvalue buckling analysis and experiment, with the single thin-walled box structure as the research object. Both the theoretical calculation and experimental results show that with reinforcement the instability ultimate load has been evidently improved and thus it is an effective method of improving the stability of box structures. The buckling form obtained by eigenvalue buckling analysis is the same as the experiment results, which can provide theoretical support for the design of reinforcement.
eigenvalue buckling analysis;stability;finite element;thin-walled box
2013-06-06
TN876.7
A
1008-5300(2013)05-0061-04
