非线性克里格法在矿体储量估算中的应用

刘修国，尤超，张唯

(中国地质大学 信息工程学院，湖北 武汉，430074)

在采矿过程中，不可避免地伴随着一些不确定因素[1]。这些不确定因素将会对矿床储量品位的估值有严重影响。可靠的矿产资源和矿床储量的估计对于所有的采矿作业都是十分重要的，不合理的矿产资源分类对项目的可行性有重大的影响。地质统计学方法通常基于随机函数而同时考虑样本数据的空间关系[2]，所以，它能够有效地对储量参数(品位、厚度和累积量)空间分布进行研究。地质统计学方法一般被分为线性克里格，非线性克里格、非参数克里格和随机模拟等[3]。由于线性克里格的平滑效应，它有时不能准确地预测待估点属性值是否超过某一阈值。相反地，非线性克里格与非参数克里格方法(多元高斯克里格和指示克里格)则可以利用条件概率分布对这些待估点进行较准确估值[4]。本文作者将选择某铜矿区实际数据作为实验数据，并利用指示克里格和多元高斯克里格2种非线性克里格方法进行研究与应用，研究主要包括 2部分内容：(1) 通过指示克里格对矿体的边界进行圈定；(2) 利用多元高斯克里格估算矿体的品位值。为了进行对比，将应用有矿化带边界的普通克里格的估值方法和无矿化带边界的多元高斯克里格估值方法对同一矿体进行品位估值，最后对估值结果进行讨论。

1 基本原理

1.1 指示克里格估值方法

指示克里格方法其实质就是通过一系列指示阈值，求出相应阈值对应的条件累积概率分布，并用条件累积概率分布表示位置点Z(u)的不确定性概率模型。指示克里格估值首先需要对数据进行指示变换，即先选择1个阈值，一般为矿体的边界品位Z。其指示化的公式如下：

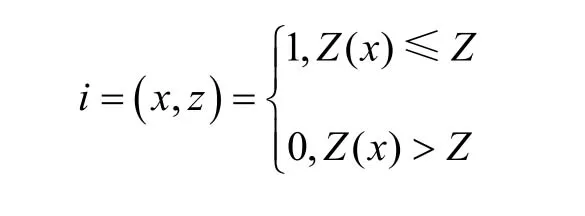
指示变换后得到一组以0和1形式组织的指示化数据。利用这组指示化数据，可对待估区域内平均值在某一范围中的概率进行估计，其原理如下。

设在待估位置u处出现阈值小于或等于Z的概率为F(u,z)，P表示概率，E(u,z)表示在待估位置u处出现阈值小于或等于z的数学期望，可得到关系式如下：

根据数学期望的求取公式可得：

其中：F(u,z)为未知点u处出现品位zu小于或等于阈值Z的累积概率。

1.2 多元高斯克里格估值方法

多元高斯克里格估值方法是对原始样品数据进行正态变换，用变换后的数据进行线性克里格估值，再对结果进行逆变换。正态变换后y(ua) =φ(z(ua))被定义为正态点数[5]。多元高斯克里格估值方法是建立在多元高斯分布假设基础之上的。原始变量在待估位置u处的条件累积分布函数(ccdf)为

在多元高斯克里格模型下，在位置u处ccdf的平均值和方差分别等同于正态点数y(ua)的普通克里格估值的均值(u)和方差(u)。因此，在位置u处的条件累积分布函数为[6]

式中：μOK(u)为拉格朗日乘数；普通克里格权重(u)和误差(u)可由普通克里格方法计算得到。Y(u)的期望值可表示为

式中的估计值即为地质统计学多元高斯克里格的估计值。

2 研究矿区概况

研究矿床是以铜为主的铜锌硫化物矿床。该铜锌矿共由2个矿体组成，编号分别为Ⅰ和Ⅱ矿体。Ⅰ矿体总体呈南北向展布，总体形态为透镜状，呈隐伏—半隐伏状产出，地表有铁帽覆盖；产于细碧岩与石英角斑质火山碎屑岩之间的接触面上[7], 由于矿体类型不同，故矿体品位的空间连续性也大不相同，所以，对于不同矿体应分别采用不同模型进行储量估算。由于Ⅰ矿体倒转翼厚度较正常翼大，矿体厚度变化比较稳定[8]，故本文以Ⅰ矿体的倒转翼为研究对象。

Ⅰ矿体倒转翼原始取样数据为3 271个，铜品位最小值为0，最大值为14.85%，平均品位为2.37%。图1所示为原始样品数据的直方图。从图1可看出：原始数据为单峰分布，并且存在拖尾现象。

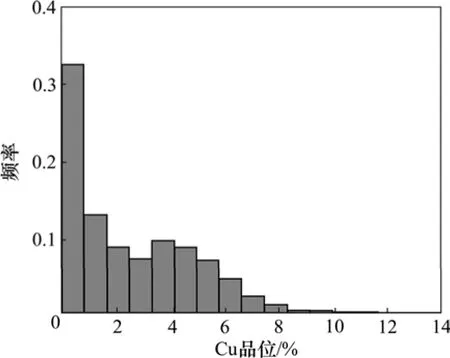
图1 原始数据样品直方图Fig.1 Histogram of original sample

3 圈定矿体边界

在进行矿体储量估算之前，首先需要圈定矿体。 在这种情况下，指示概率模型可用于确定矿体的边界；利用指示概率模型进行矿体边界的确定包括 2个主要步骤：(1) 对数据进行指示变换，利用变换后的数据采用普通克里格方法计算待估点的条件累积概率函数的估计值，也就是每一个待估点大于指示品位的概率；(2) 根据已经得到的每个待估点大于边界品位的概率，并同时考虑矿体的连续性，确定1个用于标识矿和非矿的阈值对矿体进行圈定。

3.1 指示概率模型

将概率模型应用于确定矿体边界之前需要对数据进行指示变换，指示变换后得到一组以0和1形式组织的指示化数据。利用这组指示化数据，可对待估区域内平均值在某一范围内的概率进行估计。本研究将边界品位 0.3%作为指示品位，将小于或等于 0.3%的品位设定值为1，而对大于0.3%的品位设定值为0。然后，利用这组指示化数据进行实验变差函数分析。在矿体主要的各向异性方向上，理论变差函数与实验变差函数套合图形如图2所示。

3.2 定义阈值

对矿体进行块体划分，块段长×宽×高设置为10 m×10 m×10 m。利用指示化数据，根据得到的实验变差函数进行普通克里格估值，每个块体估值后的结果为0～1之间的值。在指示克里格估值之后，需要确定一个阈值来划定块体是否属于矿化块。本研究取块体品位大于0.3%的概率为0.25的水平值作为阈值。将指示值大于0.25的块体归入的块体类；将指示值小于0.25的块体舍去。此方法圈定的矿体保持了空间分布性与地质成矿作用的特征。用指示概率模型得到的矿体边界三维模型如图3所示。

4 矿体储量估算

用指示概率模型确定了矿体边界之后，再利用多元高斯克里格对矿体储量进行估值。矿产资源储量估算可按如下步骤进行。

4.1 正态点数变换

图2 指示变差函数图Fig.2 IK variogram map

图3 矿体边界三维模型Fig.3 3D domains model

4.2 正态点数数据的变差函数分析

正态点数数据用于连续性的分析中。首先，从主要的各向异性方性计算正态点数数据的实验变差函数。其中，理论变差函数与实验变差函数的拟合图形如图4所示。根据正态点数变换的定义，各方向上的理论变差函数的基台值都等于1。

4.3 高斯克里格矿体储量估算

根据3个各向异性方向上的理论变差函数，用高斯克里格估值方法对矿体储量进行估算。同样，块段长×宽×高设置为10 m×10 m×10 m，其中搜索椭球的方位角为110°，倾伏角为20°，倾角为0°。用已知的数据进行交叉验证分析，误差平均值为0.032，标准中误差为1.011，由此可说明多元高斯克里格估值过程中变差函数的参数选择较合理。

5 结果与验证

按照不同的边际品位，用多元高斯克里格法分别计算矿石储量，结果见表1。

为了比较，分别将有矿化带边界的情况下用普通克里格方法和无矿化带边界的情况下用多元高斯克里格方法对同一矿体进行估值计算，得到平均品位—边际品位曲线对比图，如图5所示。综合分析图5可以看出：用普通克里格估值方法得到的平均品位明显低于多元高斯克里格估值方法得到的平均品位(有矿体边界和无矿体边界)；而在低边际品位和高品位位置，普通克里格方法得到的平均品位与多元高斯克里格方法得到的平均品位有更大差异；同时，在边际品位大于 1.5%时无矿体边界的多元高斯克里格方法与有矿体边界的多元高斯克里格方法得到的平均品位较相近。从对比结果可以看出：由有矿化带边界的多元高斯克里格估值方法得到的估值矿体储量更接近于实际的矿体储量。

图4 正态点数数据各向异性方向上的变差函数Fig.4 Main anisotropy directions of semi-variogram of normal scores data

表1 多元高斯克里格估值结果Table 1 Results of multi-Gaussian Kriging

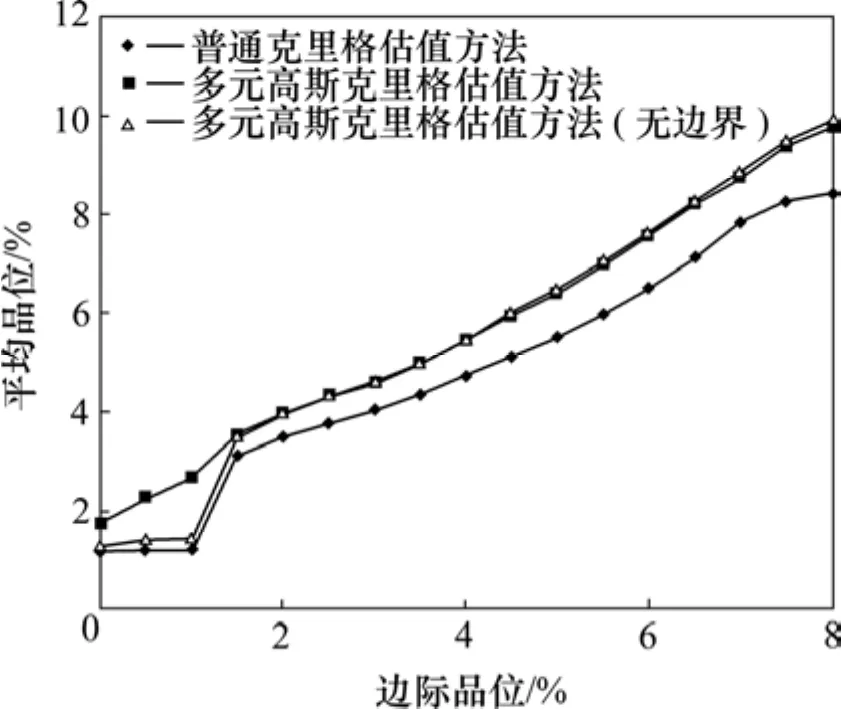
图5 平均品位—边际品位曲线对比图Fig.5 Comparison of result of CutOff-Grade

6 结论

(1) 指示概率模型是圈定矿体的一种有效方法。

(2) 无矿体边界的估值会因为无限制的平滑效应而增大估值结果的误差。

(3) 普通克里格的非平稳性和平滑效应在某种程度上也会影响储量估值的准确性，而有矿化带边界的多元高斯克里格方法得到的储量估值更加接近于实际矿体储量，从而验证了多元高斯克里格是一个简单有效的储量估值方法。

[1] Bastante F G, Taboada J, Alejano L R. Evaluation of the resources of a slate deposit using indicator Kriging[J].Engineering Geology, 2005, 81(4): 407-418.

[2] Ahmet D A G, Bayram A. Evaluating thickness of bauxite deposit using indicator geostatistics and fuzzy estimation[J].Resource Geology, 2008, 58(2): 188-195.

[3] Glacken I M, Snowden D V. Mineral resource estimation, in mineral resource and ore reserve estimation: The AussIMM guide to good practice[M]. Melbourne: The Australian Institute of Mining and Metallurgy, 2001: 189-198.

[4] Emery X. Uncertainty modeling and spatial prediction by multi-Gaussian Kriging: Accounting for an unknown mean value[J]. Computers & Geosciences, 2008, 34(11): 1431-1442.

[5] Goovaerts P. Comparative performance of indicator algorithms for modeling conditional probability distribution functions[J].Mathematical Geology, 1994, 26(3): 389-411.

[6] Emery X. Ordinary multigaussian Kriging for mapping conditional probabilities of soil properties[J]. Geoderma, 2006,132(1/2): 75-88.

[7] 张新宇, 肖克炎, 刘光胜, 等. 阿舍勒铜矿可视化储量计算的指示克里格法应用研究[J]. 吉林大学学报: 地球科学版, 2006,36(2): 305-308.

ZHANG Xinyu, XIAO Keyan, LIU Guangsheng, et al. The applied research of indicator Kriging method in visualized reserve computing of Ashele copper mine[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(2): 305-308.

[8] 李章林, 张夏林, 翁正平. 指示克里格在矿体储量计算方面的研究与应用[J]. 矿业快报, 2008, 20(1): 11-15.

LI Zhanglin, ZHANG Xialin, WENG Zhengping. Research and application of indicator Kriging method in ore body reserves calculation[J]. Express Information of Mineing Industry, 2008,20(1): 11-15.

[9] 黄竞先, 侯景儒. 泛克立格法和指示克立格法在地球化学探矿中的应用[J]. 地球科学: 中国地质大学学报, 1994, 19(3):321-328.

HUANG Jinxian, HOU Jinru. Application of universal Kriging and indicator Kriging for geochemical prospecting[J]. Earth Sciende: Journal of China University of Geosciendes, 1994,19(3): 321-328.

[10] 刘修国, 李超岭, 倪平泽, 等. 可视化固体矿产储量估算方法研究[J]. 中国地质, 2007, 34: 407-412.

LIU Xiuguo, LI Chaolin, NI Pingze, et al. Study on visualization of solid mineral reserve estimation[J]. Geology in China, 2007,34: 407-412.

[11] Abzalov M Z, Humpherys M. Resource estimation of structurally complex and discontinuous mineralization using non-linear geostatitisics: Case study of a nesothermal gold deposit in northern Canada[J]. Explor Mining Geol, 2002,11(1/2/3/4): 19-29.

[12] 孙玉建. 地质统计学在固体矿产资源评价中的若干问题研究[D]. 北京: 中国地质大学地球科学与资源学院, 2008: 51-68.

SUN Yujian. A study on several issues on application of geostatistics in solid mineral resources estimation[D]. Beijing:China University of Geosciences. School of Earth Sciences and Resources, 2008: 51-68.

[13] 王全明. 我国铜矿勘查程度及资源潜力预测[D]. 北京: 中国地质大学地球科学与资源学院, 2005: 99-129.

WANG Quanming. Degrees of copper ore exploration and resources potential of copper in lower degree areas in China[D].Beijing: China University of Geosciences. School of Earth Science and Resources, 2005: 99-129.

[14] 侯景儒, 黄竞先. 地质统计学在固体矿产资源/储量分类中的应用[J]. 地质与勘探, 2001, 37(6): 61-66.

HOU Jingru, HUANG jingxian. Application of geosatistics in classification for resource/reserves of solid fuels and mineral commodities[J]. Geology and Prospecting, 2001, 37(6): 61-66.

[15] Bastante F G, Ordonez C, Taboada J, et al. Comparison of indicator Kriging, conditional indicator simulation and multiple-point statistics used to model slate deposits[J].Engineering Geology, 2008, 98(1/2): 50-59.