基于热-结构耦合等离子喷涂热障涂层循环应力分布*

陈宇慧 ，陈丹阳 ，钟舜聪 ，杨天雪 ，杨晓翔 ，涂善东 ，轩福贞

（1.福州大学 化学化工学院，福建 福州 350108； 2.漳州职业技术学院，福建 漳州 363000；3.福州大学 机械工程及自动化学院，福建 福州 350108；4.华东理工大学 承压系统安全科学教育部门重点实验室，上海 200237；5.福建省特种设备监督检验院，福建 福州 350001）

0 引 言

等离子喷涂热障涂层（TBCs）作为一种新型防护技术，在高温环境中对于保护设备部件、延长部件寿命具有显著的作用。通过采用热障涂层技术，可以在保持原有设计的基础上，减少用作叶片冷却的空气量，提高发动机推力［1］。热障涂层主要通过低热传导这一属性产生隔热性效果，降低基体温度，使基体材料在高温下运行，发动机热效率提高60%以上。目前，该技术主要应用于工业燃气轮机高温部件以及航空航天领域，已成为发展高推质比航空发动机的一项关键技术。

TBCs系统主要分为4层［2］:基体（Sub）、粘结层（BC）、氧化层（TGO）、热障涂层（TBC）。4层材料的物理、热和机械属性都有明显的差异，增加了研究这个多层材料系统的难度。其中，TGO层的主要成分是Al2O3，它是由于在操作温度下BC层的铝元素与陶瓷层中扩散的氧元素反应生成氧化铝，通常厚度为1 μm～10 μm。TGO层的生长是涂层剥落失效的重要原因。喷涂过程中产生的残余应力，界面的复杂形状，陶瓷烧结，氧化层增长，蠕变和塑性变形产生的应力再分布等原因也是TBC损坏的主要原因。

涂层间的残余应力主要是在喷涂过程中由于相变、骤冷、热膨胀系数不匹配、BC层沉积之前喷砂处理引起的。在高温工作环境下顶层陶瓷材料会发生烧结，导致材料的体积、性能发生改变，易引起平面压应力，在涂层系统中产生垂直于界面的裂纹。

目前，国内外许多学者已开展了对热障涂层失效机理的研究。M.Ranjbar-Far等人［3］模拟了氧化层与粘结层之间不同界面粗糙度对涂层残余应力分布的影响，以及氧化层不同厚度对其影响。M.Bäker［4］研究了蠕变在涂层应力再分布中的作用。Evans等人［5］总结并详细阐述了热障涂层的制备、微结构、破坏机制和若干典型的破坏形式。Gilbert［6］对热障涂层系统在热冲击下涂层的破坏情况进行了数值研究。张显程，涂善东等人［7］针对理想平面界面涂层，通过对不同涂层材料和尺寸分别进行计算，分析比较了对残余应力的影响，对实际喷涂工艺有一定指导意义。李志永［8］利用MSC.Marc研究了不同换热系数对热机耦合作用下热障涂层性能的影响，结果表明，随着内壁换热系数的增加模型中的温度随之降低，内外壁温差以非线性形式增加，并且涂层中3个主应力随着内壁换热系数的增加而增加。周益春等人［9］对热障涂层的破坏机理和寿命预测做了详细阐述，但其忽略了对流传热对模型温度分布的影响。

不同于前人的研究工作，本研究在热计算过程中考虑了以下几点内容:

（1）温度分布方式。其中由系统上下表面通过与周围热环境进行对流传热，施加热载荷；同时各层间通过热传导进行温度传递，导致涂层系统内的温度非线性分布，并且结构计算时每层材料物理属性随温度线性变化，这些因素的共同作用使涂层内应力呈高度非线性分布；涂层上表面与环境的对流传热更符合涡轮机一级静叶片的实际工作情况。

（2）当材料长时间处于高温状态时，会发生蠕变同时伴随应力松弛；选用Norton蠕变模型，当温度高于600℃时，开启蠕变计算。

（3）采用有限元瞬态计算，连续模拟“升温-恒温-降温”过程，能够更好地观察应力随时间变化的规律。

1 数值模拟方法

1.1 几何模型和材料

热障涂层系统是由合金基体、NiCoCrAlY粘结层、氧化层、等离子喷涂氧化钇含部分稳定氧化锆（ZrO2-8 wt%Y2O3）的顶层组成。各层厚度分别为1 mm、0.1 mm、1 μm和0.25 mm。由于制造工艺原因，TBC/BC界面是粗糙的，呈凹凸的形状分布，在数值分析时把界面简化成理想的正弦波，为了降低计算时间，截取其中一段进行计算，左侧采用对称约束，右侧采用多点耦合控制约束［10］。

模型如图1所示，模拟氧化层界面采用波幅A=0.005 mm，周期T=0.02 mm的正弦波，由于模型周期对称，选取半个周期正弦进行模拟。采用间接热-结构耦合模拟计算，热计算时选用2维4节点平面应变单元Plane55，结构分析采用Plane182平面应变单元。不同温度下各层材料属性参照文献［5］中数据。

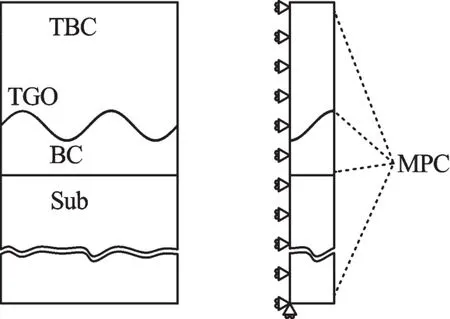
图1 微观空气等离子喷涂系统

1.2 载荷和边界条件

1.2.1 热载荷

涂层采用空气对流温度加载，表面对流换热系数的数值与换热过程中流体的物理性质、换热表面的形状、部位、表面与流体之间的温差以及流体的流速等都有密切关系。物体表面附近流体的流速愈大，其表面对流换热系数也愈大。部件服役时由于转动速度较高（例如涡轮机叶片），相对空气流速大幅提高，涂层表面对流系数可达到8 000 W（/m2·K）。本研究采用二维模型模拟汽轮机叶片横截面，对流换热，第1阶段在热障涂层外表面先以对流方式施加热载荷经过300 s达到1 300℃；第2阶段恒温2 h；第三阶段再300 s内从1 300℃降温到室温25℃，冷却通道内表面300 s内升高到400℃。恒温2 h，最后同样冷却到室温。涂层上表面换热系数选为8 000 W（/m2·K），基体内表面为600 W（/m2·K）～5 000 W（/m2·K）之间变化［11］。本研究内表面选用2 000 W（/m2·K）。得到结果涂层上表面温度达到1 177℃，内表面892℃，上下表面温差达到285℃，TBCs系统沿径向温度分布如图2所示。从图2中可明显观察到热障涂层的隔热效果。

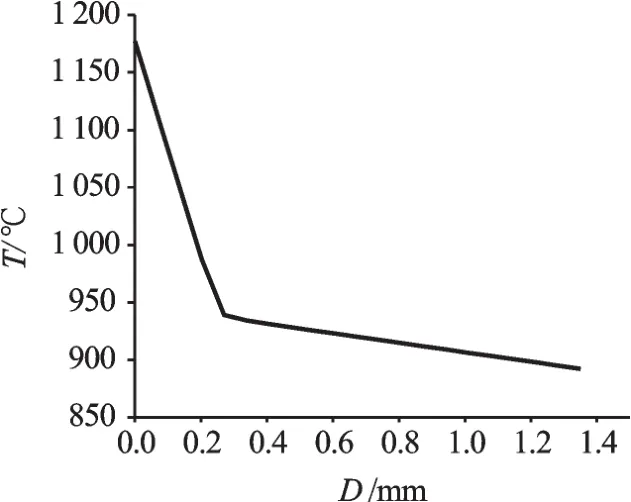
图2 TBCs系统沿径向温度分布

1.2.2 结构载荷

本研究对截取模型左端进行对称约束；右端施加周期性边界条件，采用多点耦合约束，确保其左侧和右侧在变形时保持一致。

左侧的对称约束使得在发生应变变化时，保持在一个直线上运动，右侧用多点耦合，是确保在发生位移的时候各层的变化是一致的，也是在一条直线上，这样确保左侧和右侧的位移是一致的，从而确保边界位移的连续性。

1.3 热循环过程中蠕变-Norton模型

热循环过程中蠕变的模拟选用Norton模型进行计算，材料参数如表1所示。

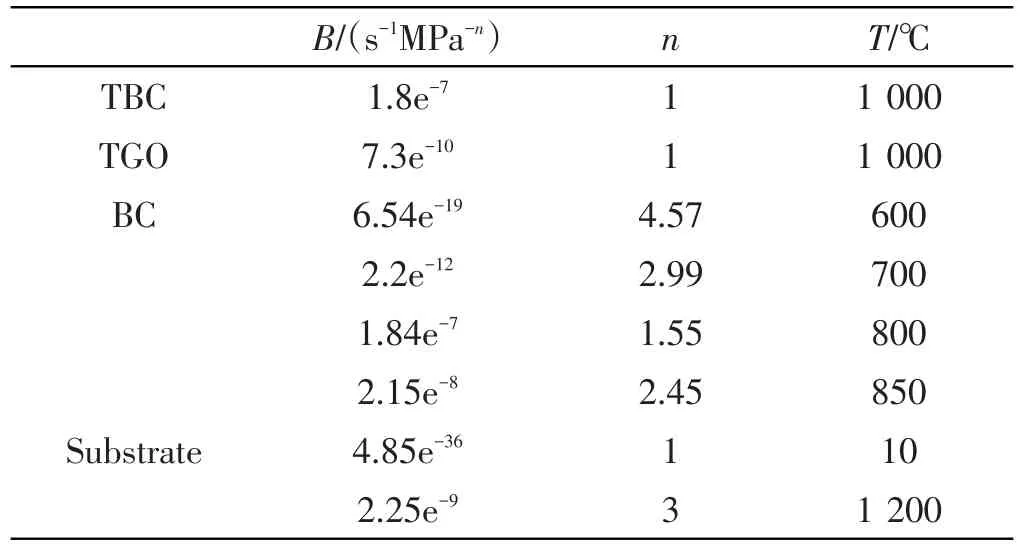
表1 各层蠕变参数

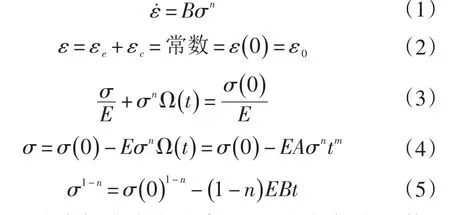
式中:ε˙—稳态蠕变应变速率；B—材料蠕变系数；σ—等效应力；n—材料蠕变指数；εe，εc—弹性应变和蠕变应变；ε0—初始应变量。

2 结果与讨论

2.1 提取S22应力作为判断依据

一般地，正常的应力分量S11、S22更容易导致I型断裂，而S12更容易引起断裂模式II的发生，本研究工作不分析S12对TBCs的影响。另一方面，导致TBC分层的裂纹是由于界面和薄层间的S22这个分量的影响，而垂直的裂纹是由于S11这个分量产生的。本研究将对在层内裂纹及TGO/BC界面存在的横向裂纹扩展的模型进行模拟。由于这些原因，S22被认为是与目前数值模拟研究工作相关的应力分量。

通常认为，陶瓷层断裂与否主要取决于陶瓷层中最大拉伸主应力是否超过其抗拉强度［12］。本研究考虑了正弦形式的氧化层界面，应力情况较复杂，但从结果上来看，其剪切应力与正应力比较影响较小，本研究不对主应力大小及方向进行研究，而对TBC中的S22应力分量进行研究。

2.2 蠕变影响

在升温和恒温过程结束后，如果不考虑蠕变，TGO层应力值范围为-343 MPa～1 380 MPa。当加入蠕变分析时，TGO层应力有所下降，应力范围为-62.6 MPa～26.6 MPa；BC层应力范围为-3.2 MPa～5.7 MPa，应力水平明显下降。

氧化层应力分布图如图3所示。

图3 恒温过程TGO层应力分布图

2.3 完整热循环后氧化层和粘结层应力分析

在升温、恒温和降温过程结束后氧化层和粘结层应力分布如图4所示。图4中，最大应力出现在粘结层波峰处，同样氧化层最大应力也出现在波峰处。一个热循环耗时7 800 s，由于高温恒温过程蠕变应力松弛导致应力大幅降低。

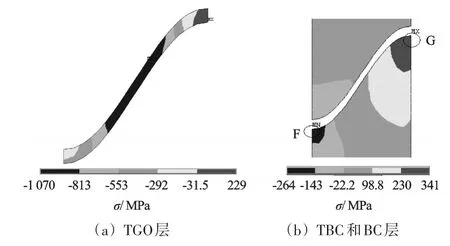
图4 一个完整热循环后各层应力分布图

2.4 不同氧化层厚度对最大应力的影响

热障涂层在服役时，氧化层会随时间增厚，但增厚到一定程度时这种行为会停止，这是由于致密的氧化层阻止了粘结层的铝离子和外界的氧离子的扩散。但随着氧化层的增厚会引起体积的增大以及各层应力的重新分布。研究结果表明，当氧化层的层厚增大的一定厚度时，会引发涂层的屈服与断裂，因此控制氧化层的厚度对保护热障涂层，提高热障涂层使用寿命起着重要的作用。由模拟数据可以观察出当TGO厚度小于3 μm时，各层应力波动较大。当厚度大于3 μm时，TGO和BC层应力小幅增长，而在TBC和Sub层应力变化不明显，各层最大应力随氧化厚度变化关系如图5所示。

2.5 完整热循环与单独降温过程结果比对

完整热循环过程包括:加热、恒温、降温过程。在恒温阶段时，蠕变可以使应力松弛，这是由于在加热的结束阶段TGO层的增长而产生一个类应力自由状态。与单独降温过程相比，最大拉应力相近。

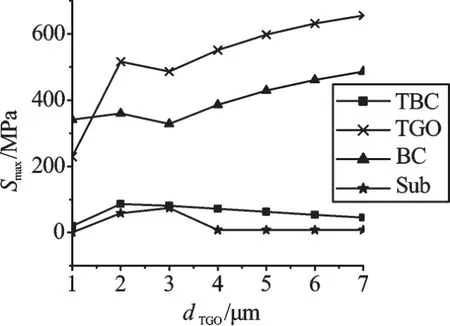
图5 各层最大应力随氧化厚度变化关系

表2 完整热循环与单独降温过程模拟应力

如表2所示，TGO层完整热循环时最大拉应力为229 MPa，最大压应力为-1 070 MPa；而单独降温过程时，最大拉应力为361 MPa，压应力为-1 160 MPa。BC层内两种情况最大应力分别为341 MPa，414 MPa，而两层内压应力较为相近分别为-264 MPa和-303 MPa。本研究的结果与Rosler等人［13］研究相吻合，表明失效通常发生在降温阶段，此时蠕变影响较小。因此，对热障涂层应力研究可以假设在高温结束时系统处于应力自由状态，主要关注冷却降温阶段。

3 结束语

通过对等离子喷涂制备的热障涂层系统建模，本研究将其界面形状简化成正弦波，能够更好地模拟涂层系统的界面粗糙度，观察凹和凸区域的应力变化。本研究采用热-结构耦合计算，通过对流和热传导方式进行温度传递，计算结果更贴合实际情况；完善了热障涂层模拟过程中模型形态与传热方式，为涂层断裂分析提供了一种前期建模方案。

研究过程中发现，恒温过程中蠕变应力松弛，应力大幅减小，致使应力的产生主要集中在降温过程；一个热循环结束后，TGO层和BC层应力较大，最大应力出现在BC层波峰区域，可以达到341 MPa；随着氧化层增厚，氧化层和粘结层应力都随之增加，最大应力出现在TGO层内达到656 MPa，粘结层达到486 MPa；膜/基结合力大幅下降，易引发裂纹萌生与扩展。

在今后的研究中，笔者将重点研究由于温度、氧化、蠕变等因素，在耦合条件下产生残余应力对裂纹的萌生与扩展过程的影响，以达到更好的预测效果，为实际生产过程中缺陷检测提供依据。

（References）:

［1］唐家鹏，李志永.涡轮叶片等离子涂层应力分析［J］.弹箭与制导学报，2010，30（6）:227-229.

［2］PADTURE N P，GELL M，JORDAN E H.Thermal barrier coatings for gas-turbine engine applications［J］.Science，2002，296（4）:280-284.

［3］RANJBAR-FAR M，ABSIA J，SHAHIDIB S，et al.Impact of the non-homogenous temperature distribution and the coatings process modeling on the thermal barrier coatings system［J］.Materials and Design，2011，32（2）:728-735.

［4］BÄKER M，RÖSLER J，Heinze G.A parametric study of the stress state of thermal barrier coatings Part II cooling stresses［J］.Acta Materialia，2005，53（2）:469-476.

［5］EVANS A G，MUMM D R，HUTCHINSON J W，et al.Mechanisms controlling the durability of thermal barrier coatings［J］.Progress in Materials Science，2001，46（5）:505-553.

［6］GILBERT A，KOKINI K，SANKARASUBRAMANIAN S.Thermal fracture of zirconia-mullite composite thermal bar⁃rier coatings under thermal shock:A numerical study［J］.Surface&Coatings Technology，2008，20（3）:91-98.

［7］张显程，巩建鸣，涂善东，等.涂层材料与几何尺寸对等离子喷涂残余应力的影响［J］.南京工业大学学报，2003，25（1）:63-67.

［8］李志永，鲍 蕊，张建宇，等.换热系数对热机耦合作用下热障涂层性能的影响［J］.航空动力学报，2008，23（5）:5946-5951.

［9］周益春，刘奇星，杨 丽，等.热障涂层的破坏机理与寿命预测［J］.固体力学学报，2010，31（5）:504-531.

［10］RANJBAR-FAR M，ABSIA J，MARIAUXC G，et al.Simula⁃tion of the effect of material properties and interface rough⁃ness on the stress distribution in thermal barrier coatings using finite element method［J］.Materials and Design，2010，31（2）:772-781.

［11］曹玉璋，陶 智，徐国强，等.航空发动机传热学［M］.北京:北京航空航天大学出版社，2005.

［12］XIE Wan-gang，JORDAN E，GELL M.Stress and cracking behavior of plasma sprayed thermal barrier coatings using an advanced constitutive model［J］.Materials Science and Engineering:A，2006，419（1-2）:50-58.

［13］ROSLER J，BAKER M，AUFZUG K.A parametric study of the stress state of thermal barrier coatings:part I:creep re⁃laxation［J］.Acta Materialia，2004，52（6）:4809-4817.