智能复合材料风力机叶片设计与有限元分析

乔印虎，韩 江，张春燕，陈杰平

（1合肥工业大学 机械与汽车工程学院，合肥 230009；2安徽科技学院 机电与车辆工程学院，安徽 凤阳 233100）

风力机叶片占整机成本的25%～28%左右，随着风力机的大型化，在作大范围空间旋转的柔性叶片弯扭耦合变形及气动力与弹性变形的耦合往往造成颤振［1，2］。在风力机叶片的保护上，现在使用的振动保护仪，是一种被动保护方式，当风过大时顺桨或停机［3］。随着自适应材料的出现和控制技术的发展，新的智能结构出现了，这种结构在使用中会随着操作环境的变化而改变自身的特性和布局，达到主动适应外部环境的目的。压电材料具有将电能和机械能进行双向可逆转换的性质，既可以用作传感器又可以用作致动器，同时，压电材料还具有质量轻、能耗小、响应快、易成型、稳定性好等特点，是目前研究和使用最为广泛的智能材料之一。将压电材料粘贴于各向同性以及各向异性梁、板、壳等结构的表面或嵌入其内部，通过压电单元的正、逆压电效应，达到空间结构形状控制以及柔性结构振动主动／混合控制的目的。对压电智能结构中致动、传感等物理现象的研究无疑将会导出一系列偏微分方程。一般说来，当边界条件或求解域较复杂时，求得这些偏微分方程的精确分析解是比较困难的，因此，当需对某些问题进行详细的分析、研究时，数值分析方法便成为第一选择。随着计算机技术的发展，有限元方法已成为解决工程问题最重要的数值分析工具之一，并在压电智能结构的分析与仿真研究中占有重要地位［4］。有关飞行器颤振主动抑制方面的研究报道较广泛。但已有的研究主要是针对实心截面梁类结构［5］，孙立宁等［6］和 Maheri等［7］从压电材料的非线性本构关系、基于Hamilton原理和模态控制理论，推导压电复合材料结构的有限元动力方程，利用压电材料进行复合材料结构振动控制。通过控制作用在压电材料上的电压，达到振动控制的目的。在过去的10年中，已经有大量关于采用分布式传感器／作动器的智能结构对轻质结构进行控制的研究。Sarangi等［8］用有限元建模，加上边界条件，在时域中采用直接速度反馈控制构成闭环系统，施加电压对结构进行振动控制。Victor等［9］对自适应压电复合材料进行了设计和建模，并通过调整压电片的位置进行优化。Garc等［10］和Lin［11］考虑各种边界条件，采用层压理论建立通用有限元法方程分析压电层合板的位移，并与三维、闭环结构的解进行比较。Correia等［12］采用混合层压理论，由有限元方法分析了压电壳体的振动控制问题，通过半圆壳体仿真发现控制效果良好。Tzou等［13］研究了分布有压电驱动器的锥壳的有限元建模和控制，由电场力和机械力共同作用于系统，建立了方程，并由电场力控制系统的振动。Li等［14］考虑在锥壳表面粘贴压电传感器，分析不同情况下传感器信号的采集问题。从以上文献可以看出，智能风电叶片的研究才刚刚兴起，现有的研究大体上是基于圆柱壳体或圆锥壳体进行近似分析，其控制方法、控制效果也在研究中。本工作采用压电主动约束层阻尼结构，满足风力机叶片振动保护的动作快速性要求，利用埋入复合材料结构的压电传感器和压电驱动器制成夹心材料对其振动进行主动控制。

1 风力机叶片的设计

1.1 风力机直径、叶尖速比、叶片数和翼型的确定

采用Pro／E与EXCEL软件相结合的方法进行风力机叶片的三维建模，主要包括以下步骤：（1）根据设计的风力机功率，计算风轮直径，得到叶片设计长度；（2）为了简化叶片设计，选择一种常用的翼型；（3）在EXCEL中，根据翼型以及叶片截面数据，确定各叶素截面的弦长、扭角以及截面到旋转中心的距离；（4）根据叶片数据，在Pro／E中生成截面、放样，完成建模。风力机直径通常根据所设计风力发电机的功率，利用公式（1）来确定［15］：

式中：P为所设计的风力机功率（11kW）；V1为设计的额定风速，这里为无限远来流速率（8m／s）；D为风轮直径；CP为功率系数，实际中达不到贝茨理论得出的0.593，根据国内外多种风力机的设计取0.4；η1，η2分别为电机效率与传动效率。由于小型风力发电机风轮的转速较高，总的效率较高，因此取η1·η2＝0.9，计算并圆整后得出风轮直径D＝11m。一般小型风力机为高速风轮，叶尖速比系数较高，本工作将叶尖速比确定为λ＝6。由于3个叶片风力机的运行和输出功率较为平稳，目前采用3个叶片的风力机较多。考虑风轮叶尖数与尖速比的匹配关系，对于叶尖速比λ＝6的高速风轮，将叶片数确定为B＝3。现代设计叶片时大都选择成熟的翼型，翼型根据使用情况可以分为传统翼型和风力机专用翼型。翼型选用NACA4412，其最大厚长比为12%，气动中心在距前缘30%处。通过查表及以上各式的计算［15］，可以确定风力机叶片各个参数，则叶片的几何形状就可以确定了，同时叶片的实际扭转角θi也可确定，如表1所示。

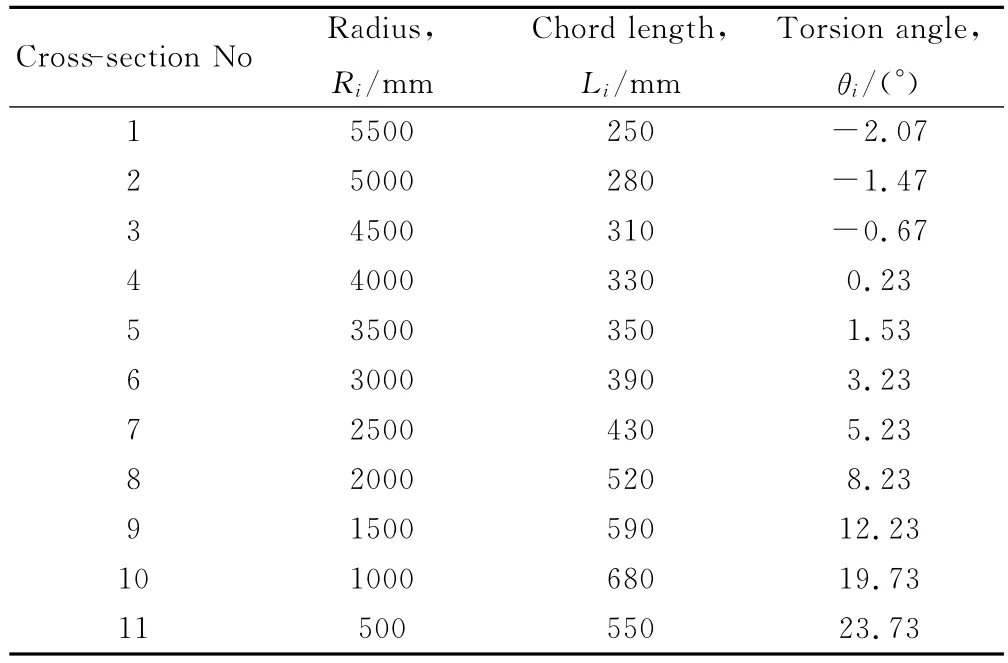
表1 叶片各截面参数Table 1 The parameters of blade each cross－section

1.2 叶片各叶素空间坐标的求解

由Profili软件获得原始翼型数据（X0，Y0），原始翼型弦长为100mm，以弦长为X轴，以前缘为原点，以有限个坐标点来描绘翼型形状。根据不同的设计需要选取翼型。翼型数据及其气动性可参考Profili软件，从Profili软件导出翼型数据，得到NACA4412.DAT文件，在EXCEL中实现坐标转换，并保存。图形变换的实质是对组成图形的各顶点进行坐标变换，运用齐次坐标的方法，可将三维空间点的几何变换表示为：

其中，T是4×4阶的变换矩阵，即

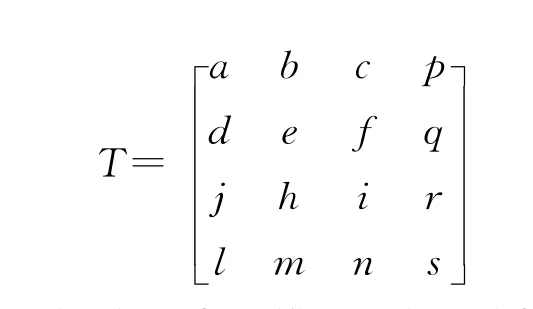
其中左上角子矩阵产生三维图形的比例、对称、错切和转换变换，左下角子矩阵产生平移变换，右上角子矩阵产生透视变换，右下角子矩阵产生全比例变换。首先建立三维空间坐标系：取R＝0的叶片截面为XOY平面，取该截面的气动中心为原点O，弦线前缘到后缘为X轴正向，垂直于弦线指向上翼面为Y轴正向，翼展方向为Z轴正向。基于点坐标的几何变换理论求解叶片各截面在上述坐标系的三维坐标。所选翼型的气动中心在距前缘30%弦长的弦线上，X1＝X0－0.3，Y1＝Y0，进而，得叶片截面空间坐标。在EXCEL中可以写成公式（3）的形式：

将修正后的各个截面弦长Li和扭角θi以及所选翼型的原始上下翼面坐标（X0，Y0）代入叶片截面空间坐标求解方程，就可求得各个截面在上述坐标系的三维空间坐标。叶片设计程序计算得到的设计结果是m个截面所有离散点的空间坐标（X，Y，Z），数据量非常庞大，通过EXCEL可实现上述坐标转换。利用以上函数公式（3）自动得到某个截面的所有变化，然后按照同一个模式只需改变原始参数就可自动得到所有空间数据。避免复杂的计算量，基于其得到的截面空间转化结果数据，方便下一步三维建模的数据整理。

2 基于Pro／E的叶片设计与建模

2.1 风力机叶片建模方法

在EXCEL中实现坐标转换，并保存，得到IBL格式的文件，利用Pro／E中的高级曲面功能可直接读入记录有数据点信息的IBL格式文件，得到叶素分布图如图1所示，再利用“边界混合工具”，依次选取各叶素曲线，得到叶片曲面。叶片曲面造型完成后，此时生成的叶片仅仅为没有厚度概念的曲面造型（如图2所示），还不是实体模型，自动混合成曲面模型，封闭模型后，即可转换为实体模型。需要根据叶片结构对其进行加厚铺层处理，经过曲面的加厚处理后，就可得到叶片的三维实体模型。

2.2 叶片造型后处理

此时的叶片并没有完全满足使用要求，应根据实际的使用要求在此基础上设计叶片的其他部分，主要为叶尖部分和叶根部分，叶尖采用离其最近的翼型进行1／2缩小，主要起到改善叶尖气流的作用，叶根是将叶片连接到轮毂上的部分，其结构要根据风机轮毂结构而定，本工作将叶根设计成圆柱形，在其上钻孔并通过螺栓与轮毂法兰盘上的孔连接，实现叶片的固定，如图3所示。

图3 叶片外形Fig.3 Blade shape

3 叶片的智能夹层结构设计

大型风机叶片目前基本采用玻璃纤维增强塑料（GFRP）制造，由蒙皮和主梁组成，蒙皮采用夹芯结构，中间层是硬质泡沫塑料或Balsa木，上下面层为GFRP。对于玻璃钢／压电材料这种各向异性材料，当外力方向不在弹性主轴方向上时，正应力将会引起剪应变，剪应力将引起线应变这一在各向同性材料中不存在的现象，为了与各向同性材料中的一般应变有所区别，称这种应变为附加应变。为了抵消这些由于附加应变而使层合板产生的弯曲或扭曲变形，按照［＋45°／－45°／－45°／＋45°］铺层。本设计选用压电材料为PZT，铺放在上下两层玻璃钢材料中间。设计的夹层叶片结构如图4所示，当遇到外界恶劣天气时，叶片发生变形、振动甚至共振，通过给压电材料施加一定的外部电压，改变叶片的振动参数，使叶片的转速下降并抑制振动的发散，消除共振和颤振。生的应力图如图9和图10所示。可以看出，压电材料产生的驱动力能够抵消叶片15m／s风速作用下的气动载荷，由于根部受力较大，应加强叶片根部的压电驱动器分布，从而能够削弱或避免叶片的剧烈破坏振动。

图4 夹层叶片结构设计Fig.4 Designed structure of sandwich blade

4 有限元分析

4.1 叶片气动流体分析

在Pro／E中建立模型10000×6000×4000的长方体作为空气流场，并将叶片装配到气流场中，保存10000.asm。在Algor中导入上一步做好的装配体文件，分析类型为稳态流体分析。收敛公差为0.0001，定义流场材料为AIR，叶片为玻璃钢复合材料，网格类型为四面体，对两个部件分别划分网格，设置边界条件。选择流场入口和出口，设定来流风速为15m／s，将叶片根部全约束。15m／s风速下的应力云图和应变图如图5和图6所示，最大应力为8.352N／mm2。

4.2 施加电场电压后的叶片减振情况

采用Algor静电分析－叶片压电材料分析，极化方向：Z，极化弹模＝横向弹模＝80000MPa，剪切模量为30769MPa，密度为7500kg／m3，泊松比为0.3。划分网格并在上下表面电极间施加400V的电压，如图7，8所示。计算结构产生的变形和应力。求解—单元定义—材料定义—求解参数—求解。点击Perform Analysis，求解结束后程序自动进入Results后处理器显示等效应力分布，显示的位移变化图和压电材料产

5 结论

（1）提出了基于压电材料的风机叶片的振动保护方案。

（2）分析了叶片的气动流体力作用下的应力和应变。

（3）设计了压电复合材料叶片，并用Algor软件分析了压电材料变形的位移量和应力的大小，与气动力作用情况进行对比，说明能用于玻璃钢复合材料叶片的振动主动控制，为进一步解决风力机叶片的气动弹性稳定性问题提供参考。

［1］BARLAS T K，Von KUIK G A M.Review of state of the art in smart rotor control research for wind turbines［J］.Progress in Aerospace Sciences，2010，46（2）：1－27.

［2］李德源，叶枝全，包能胜，等.风力机旋转叶轮振动模态分析［J］.太阳能学报，2004，25（1）：72－77.LI De－yuan，YE Zhi－quan，BAO Neng－sheng，et al.Vibration modal analysis of the rotating rotor of horizontal axis wind turbine［J］.Acta Energiae Solaris Sinica，2004，25（1）：72－77.

［3］乔印虎，朱志坚，张春燕.IIR滤波器在风力发电机振动保护仪上的应用［J］.机电工程，2007，24（2）：8－10.QIAO Yin－hu，ZHU Zhi－jian，ZHANG Chun－yan.IIR filter application in vibration guard module of wind turbine［J］.Journal of Mechanical ＆ Electrical Engineering，2007，24（2）：8－10.

［4］张晓明.风力发电复合材料叶片的现状与未来［J］.纤维复合材料，2006，23（2）：60－63.ZHANG Xiao－ming.The present and future of wind turbine composite blade［J］.Fiber Composites，2006，23（2）：60－63.

［5］杨树莲，侯志强，任勇生，等.风力机叶片气动弹性和颤振主动控制研究进展［J］.机械设计，2009，26（9）：1－7.YANG Shu－lian，HOU Zhi－qiang，REN Yong－sheng，et al.Researching headways for initiative control on aero－elasticity and flutter of wind turbine blade［J］.Journal of Machine Design，2009，26（9）：1－7.

［6］孙立宁，楚中毅，曲东升，等.压电智能结构有限元动力模型及其振动主动控制的研究［J］.高技术通讯，2004，14（11）：60－64.SUN Li－ning，CHU Zhong－yi，QU Dong－sheng，et al.Research of finite element dynamical model and active vibration control for piezo smart structure ［J］.High Technology Letters，2004，14（11）：60－64.

［7］MAHERI A，NOROOZI S，VINNEY J.Decoupled aerodynamic and structural design of wind turbine adaptive blades［J］.Renewable Energy，2007，32（10）：1753－1767.

［8］SARANGI S K，RAY M C.Active damping of geometrically nonlinear vibrations of doubly curved laminated composite shells［J］.Composite Structures，2011，93（12）：3216－3228.

［9］VICTOR M，FRANCO C，MARIA A，et al.Modelling and design of adaptive composite structures［J］.Computer Methods in Applied Mechanics and Engineering，2000，185（2－4）：325－346.

［10］GARC J S，SOARES C M M，SOARES C A M，et al.Analysis of laminated adaptive plate structures using layerwise finite element models［J］.Computers and Structures，2004，82（11）：1939－1959.

［11］LIN Jin－chen.Adaptive control of a composite cantilever beam with piezoelectric damping－modal actuators／sensors［J］.Composite Structures，2005，70（10）：170－176.

［12］CORREIA I F P，SOARES C M M，SOARES C A M，et al.A－nalysis of adaptive shell structures using a refined laminated model［J］.Composite Structures，2004，66（5）：261－268.

［13］TZOU H S，WANG D W，CHAI W K.Dynamics and distributed control of conical shells laminated with full and diagonal actuators［J］.Journal of Sound and Vibration，2002，256（1）：65－79.

［14］LI H，CHEN Z B，TZOU H S.Torsion and transverse sensing of conical shells［J］.Mechanical Systems and Signal Processing，2010，24（12）：2235－2249.

［15］陈云程.风力机设计与应用［M］.上海：上海科学技术出版社，1990.