基于按正弦周期律拓展的分数阶积分的变分问题的Noether定理*

龙梓轩，张 毅

(1.苏州科技学院数理学院，江苏苏州 215009;2.苏州科技学院土木工程学院，江苏苏州 215009)

分数阶微积分的历史可以追溯到1695年Leibniz和L'Hospital之间的讨论［1］，但是直到最近的40年间分数阶微积分在科学和工程各领域才得到广泛的应用［2－3］，包括:经典和量子力学、场论和最优控制等。1996年，Riewe［4］首先开展了分数阶变分问题的研究，提出了将分数阶微积分应用于非保守系统动力学和耗散系统的建模，初步形成了分数阶Euler-Lagrange方程和分数阶Hamilton方程。之后，分数阶变分问题得到了应用数学、物理学、动力学与控制等研究领域的众多学者的高度关注，并取得了一系列重要成果［5－9］。

为了建立非保守系统动力学模型，El-Nabulsi于2005年在分数阶微积分的框架下基于Riemann-Liouville分数阶积分定义提出了一种新的建模方法［8］，称之为类分数阶变分方法。该方法的特点在于分数阶时间积分仅引进一个实参数α，所得到的Euler-Lagrange方程形式简单且类似于经典的方程。该Euler-Lagrange方程的新颖之处在于存在一个作用在系统上的广义分数阶外力，尤其是方程中不出现分数阶导数，而仅仅依赖于分数阶积分的阶α。最近，El-Nabulsi将这种动力学建模思想进一步加以推广，提出了基于按周期律拓展的分数阶积分的类分数阶模型［9］。

对称性和守恒量的概念在物理学和数学中扮演着重要角色。对称性在数学上是用变换群来描述的，即系统在变换群作用下保持的某种不变性，它对系统的动力学行为和定性性质具有深刻影响。守恒量在变分学和最优控制方面的一个典型应用是约化系统的自由度，从而实现维数的降低和微分方程积分的简化。1918年德国女数学家Noether提出了一个定理，揭示了Hamilton作用量在群的无限小变换下的不变性与守恒量之间的潜在关系。关于动力学系统的对称性与守恒量的研究是数学、物理学、分析力学的一个重要发展方向［10－16］。最近，基于El-Nabulsi提出的类分数阶模型，我们开展了变分问题的Noether对称性研究［17－19］。本文进一步研究基于按正弦周期律拓展的分数阶积分的类分数阶模型下的Noether理论，建立了类分数阶Noether定理，给出了类分数阶Noether对称变换和Noether准对称变换的定义和判据，建立了类分数阶Noether对称性与守恒量之间的关系。本文结果具有普遍意义，不仅经典的Noether定理是其特例，而且可以进一步推广到各类约束力学系统，例如非完整系统、Birkhoff系统等。

1 基于按正弦周期律拓展的分数阶积分的类分数阶变分问题

定义1［9］设f(t)是在区间［a，b］上的连续函数。对于t∈［a，b］，按正弦周期律拓展的阶为α(α＞0)的左右分数阶积分定义为

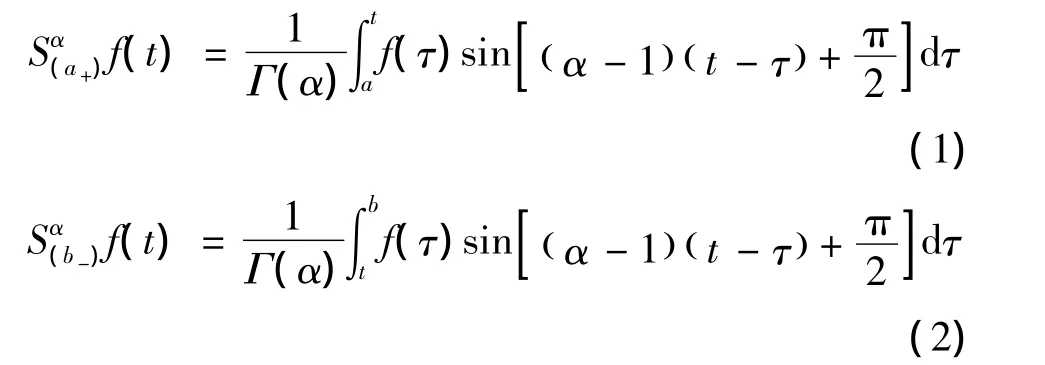
假设力学系统的位形由n个广义坐标qk(k=1，…，n)来确定，系统的Lagrange函数为L=L( τ ，q，q˙)。按照El-Nabulsi提出的非保守力学系统建模的类分数阶变分方法［9］，类分数阶变分问题定义如下:

求积分泛函

在固定边界条件

上述变分问题称为基于按正弦周期律拓展的分数阶积分的类分数阶变分问题，泛函 (3)又可称为基于按正弦周期律拓展的分数阶积分的类分数阶Hamilton作用量，当α=1时，上述问题成为经典的力学系统的变分问题。

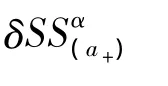
对上式第二部分分部积分，并利用边界条件 (4)，我们有

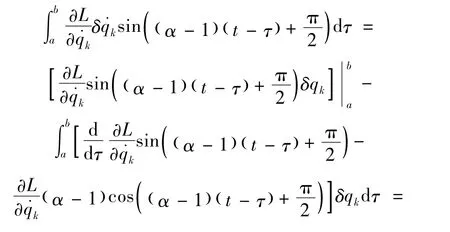
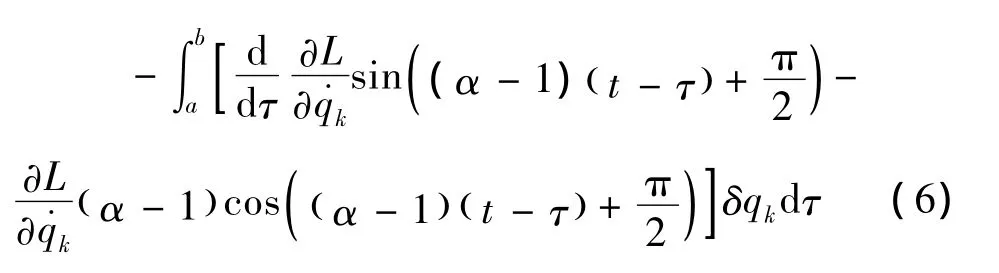
将式 (6)代入式 (5)，有

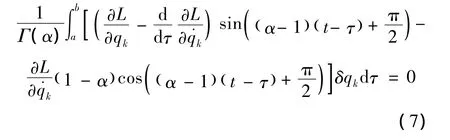
由积分区间［a，b］的任意性，我们得到

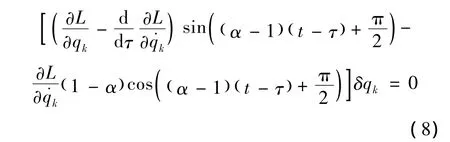
式 (8)可称为基于按正弦周期律拓展的分数阶积分的类分数阶d'Alembert-Lagrange原理。原理 (8)既适用于完整约束系统，也适用于非完整约束系统。

对于完整约束系统，δqk(k=1，…，n)是相互独立的，因此由式 (8)得出

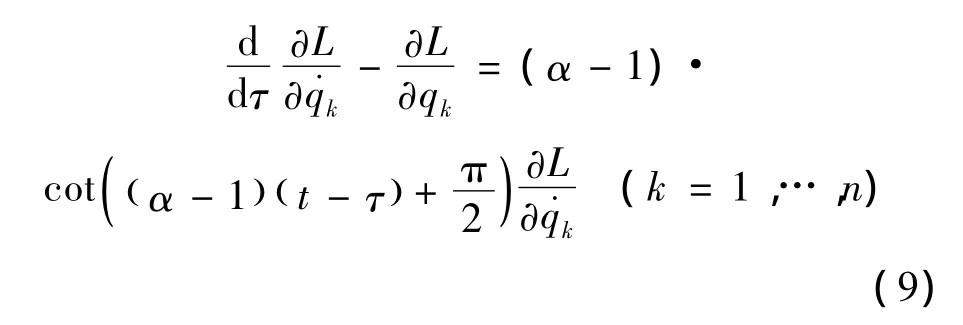
方程 (9)是完整约束系统的类分数阶Euler-Lagrange 方程［9］。

2 类分数阶Hamilton作用量的变分

引进无限小群变换

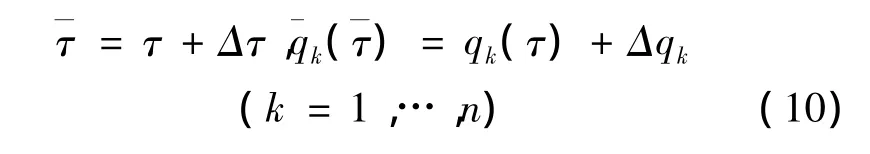
其展开式为

其中εσ(σ=1，…，r)为无限小参数，，为无限小群变换的生成元或生成函数。

类分数阶作用量 (3)在变换前后的差为

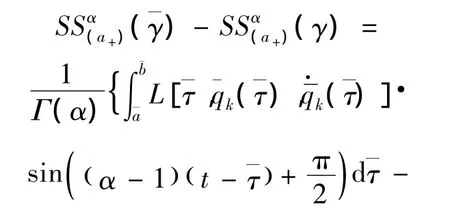
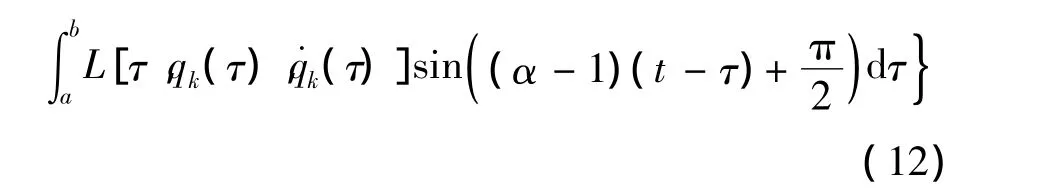
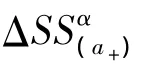
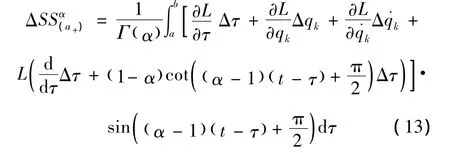
对于任意函数F，其非等时变分Δ与等时变分δ之间有关系［10］

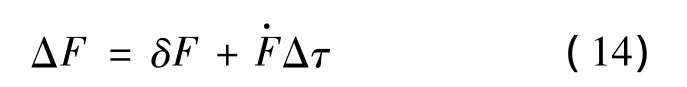
于是有

由式 (15)，式 (13)可表为

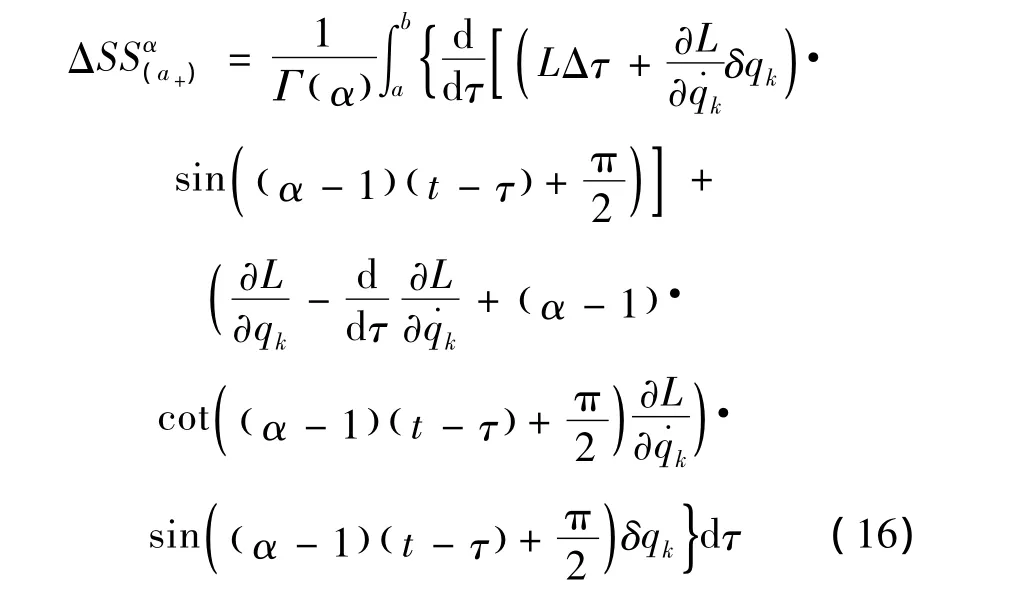
由式 (11)和 (15)，上式可进一步表为

公式 (13)和 (17)是类分数阶Hamilton作用量变分的基本公式。

3 类分数阶Noether对称变换

下面我们来建立基于按正弦周期律拓展的分数阶积分的类分数阶Noether对称变换的定义和判据。

定义2 如果类分数阶Hamilton作用量 (3)是无限小群变换 (10)的不变量，即对每一个无限小变换，始终成立

则称无限小变换是类分数阶Noether对称变换。

由定义2和变分公式 (13)，我们有如下判据。

判据1 对于无限小群变换 (10)，如果满足条件

则变换是系统的类分数阶Noether对称变换。

由定义2和变分公式 (17)，我们有如下判据。

判据2 对于无限小群变换 (11)，如果满足条件

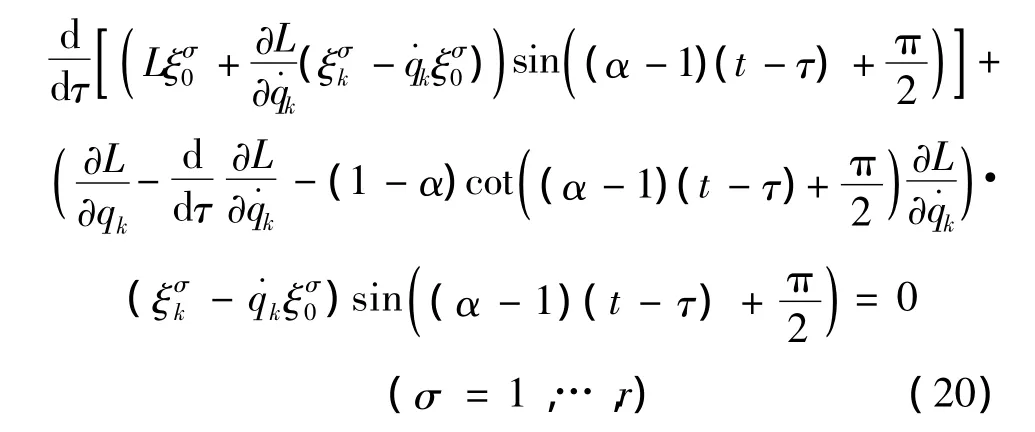
则变换是系统的类分数阶Noether对称变换。

利用关系

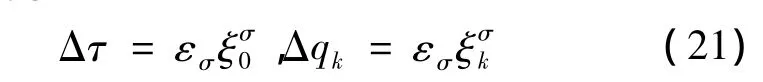
并考虑到无限小参数εσ的独立性，则式 (19)可表为r个方程

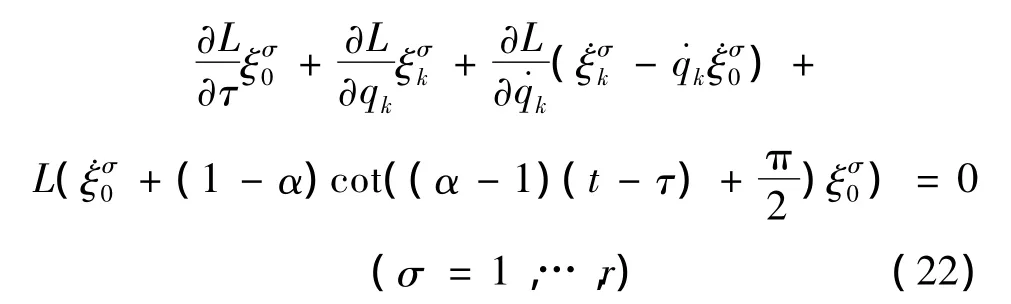
式 (22)亦可作为系统对称变换的判据。当取r=1时，式 (22)可称为类分数阶Noether等式

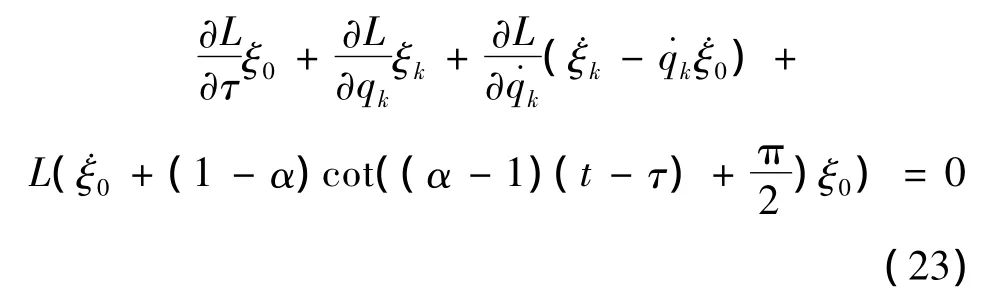
其次，我们来建立类分数阶Noether准对称变换的定义和判据。

设L′是另外的Lagrange函数，如果变换 (10)精确到一阶小量满足条件

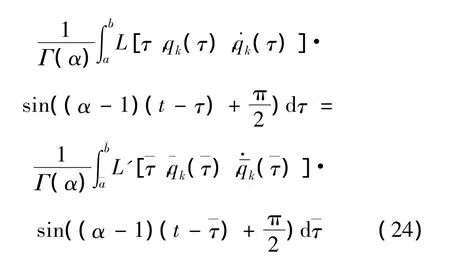
则称类分数阶Hamilton作用量 (3)是无限小群变换 (10)下的准不变量。由此确定的L′和L具有同样的运动微分方程，则变换称为类分数阶Noether准对称变换，有

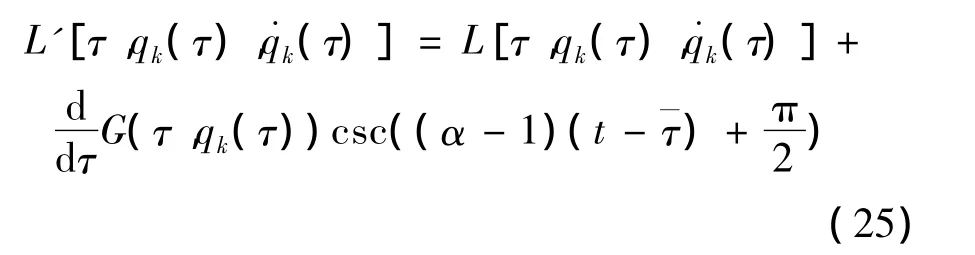
将式 (25)代入式 (24)，得到

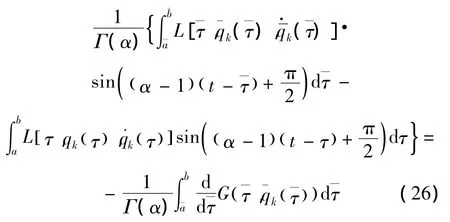
式 (26)的左端在变换 (10)下是一阶小量，因此，其右端应为同阶小量，可用ΔG代替G，而

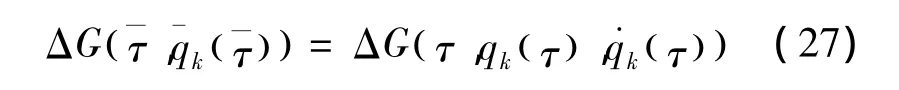
因此有

定义3 如果类分数阶Hamilton作用量 (3)是无限小群变换 (10)的准不变量，即对每一个无限小变换，始终成立

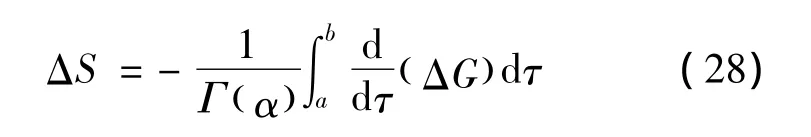
其中G=G(τ，q，)，则称无限小变换是类分数阶Noether准对称变换。

由定义3和公式 (13)，我们得到如下判据。

判据3 对于无限小群变换 (10)，如果满足条件

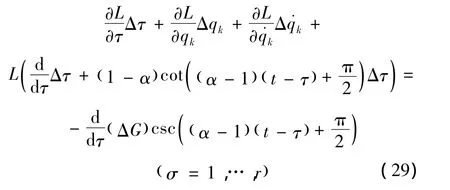
则变换 (29)是类分数阶Noether准对称变换。

由定义3和公式 (19)，我们得到如下判据。

判据4 对于无限小群变换 (11)，如果满足条件

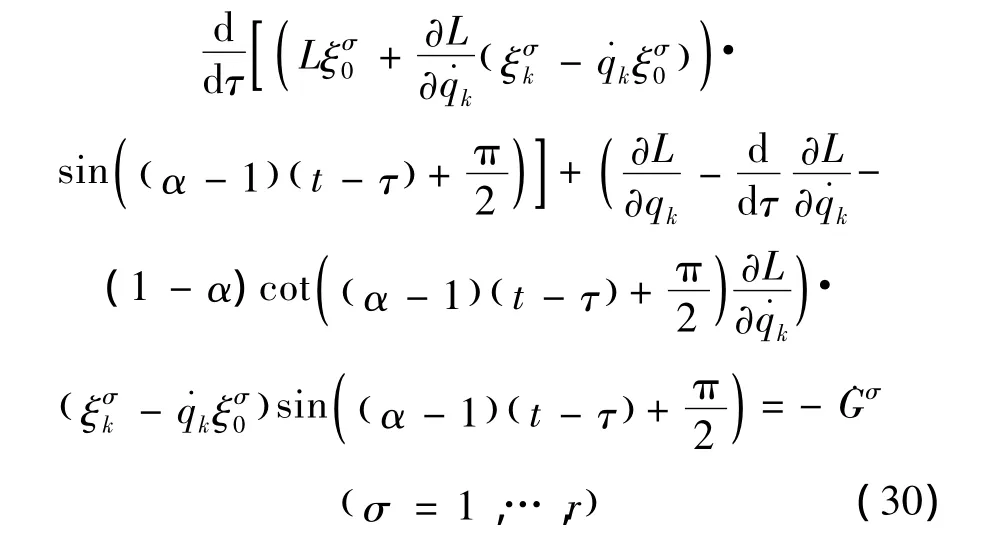
则变换是类分数阶Noether准对称变换。其中

利用关系 (21)， (31)，并考虑到εσ的独立性，则式 (29)可表为r个方程

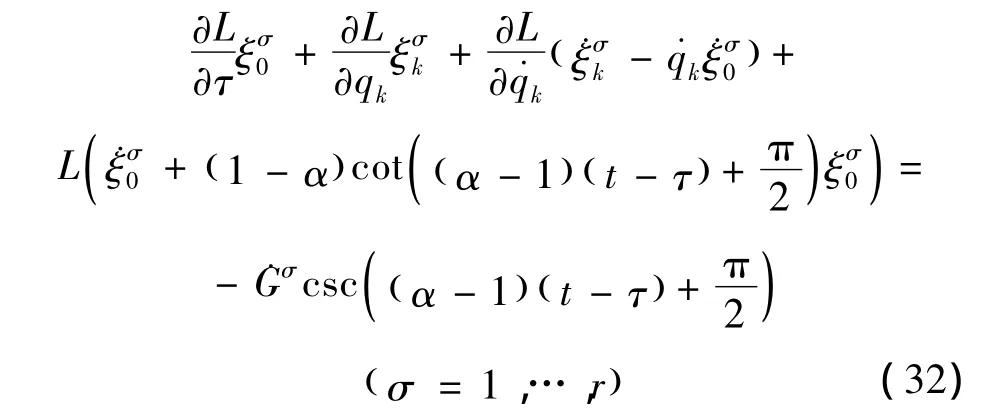
式 (32)亦可作为系统准对称变换的判据，函数Gσ=Gσ(τ，q)称为规范函数。当取r=1时，式(32)给出类分数阶Noether等式

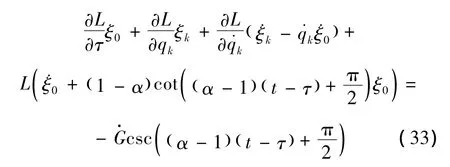
利用判据1和判据2可以判断所论系统的类分数阶Noether对称性，利用判据3和判据4可以判断所论系统的类分数阶Noether准对称性。

4 完整系统的类分数阶Noether定理

首先，基于上述类分数阶动力学模型，给出完整系统的守恒量定义。

定义4 函数Iτ，q，˙( )q称为完整系统 (9)的守恒量，当且仅当沿着完整系统的类分数阶Euler-Lagrange方程 (9)的解曲线恒成立

对于完整系统，如果能找到其类分数阶Noether对称变换或准对称变换，便可找到与之相应的守恒量。有如下定理:

定理1 对于完整系统 (9)，如果无限小群变换 (11)是定义2意义下的类分数阶Noether对称变换，则系统存在r个线性独立的守恒量，形如

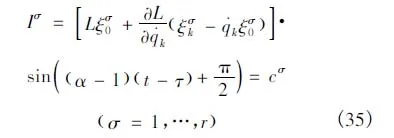
证明 因为无限小群变换是系统的类分数阶Noether对称变换，由定义2，有，即

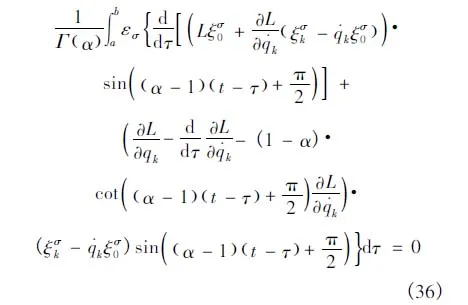
将方程 (9)代入上式，由积分区间的任意性和参数εσ的独立性，得到

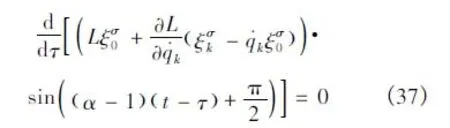
积分之，便得式 (35)。证毕。

定理2 对于完整系统 (9)，如果无限小群变换 (11)是定义3意义下的类分数阶Noether准对称变换，则系统存在r个线性独立的守恒量，形如

定理1和定理2可称为完整系统的类分数阶Noether定理。由Noether定理可知，对于完整约束系统，如能找到系统的一个类分数阶Noether对称变换或准对称变换，便有可能得到系统的一个守恒量。

例 平面Kepler问题的Lagrange函数为

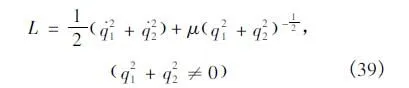
试研究其基于按正弦周期律拓展的分数阶积分的类分数阶Noether对称性与守恒量。

首先，寻找类分数阶Noether准对称变换。类分数阶广义Noether等式 (32)给出

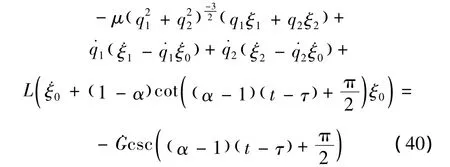
方程 (40)有解

生成元 (41)对应于系统的类分数阶Noether对称变换，生成元 (42)对应于系统的类分数阶Noether准对称变换。

由定理1，相应于生成元 (41)，系统存在如下守恒量

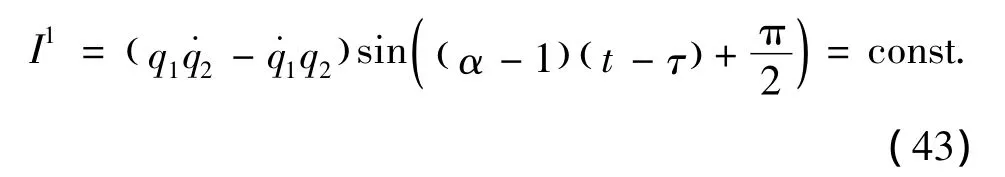
式 (43)是我们得到的系统的类分数阶Noether对称性 (35)导致的守恒量。

由定理2，相应于生成元 (42)，守恒量式(35)给出

因此，对应生成元 (42)的无限小变换是平庸的。

［1］OLDHAM K B，SPANIER J.The fractional calculus［M］.San Diego:Academic Press，1974.

［2］PODLUBNY I.Fractional differential equations［M］.San Diego:Academic Press，1999.

［3］KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and applications of fractional differential equations［M］.Amsterdam:Elsevier B V，2006.

［4］RIEWE F.Nonconservative lagrangian and Hamiltonian mechanics［J］.Phys Rev E，1996，53:1890－1899.

［5］AGRAWAL O P.Formulation of Euler-Lagrange equations for fractional variational problems［J］.J Math A-nal Appl，2002，272(1):368 －379.

［6］JUMARIE G.Fractional hamilton-jacobi equation for the optimal control of nonrandom fractional dynamics with fractional cost functions［J］.J Appl Math ＆ Computing，2007，23(1/2):215－228.

［7］ATANACKOVIC＇T M，KONJIK S，PILIPOVIC＇S，et al.Variational problems with fractional derivatives:Invariance conditions and Noether's theorem ［J］.Nonlinear Anal，2009，71:1504 －1517.

［8］EL-NABULSI A R.A fractional approach to nonconservative Lagrangian dynamical systems［J］.Fizika A，2005，14(4):289－298.

［9］EI-NABULSI A R.A periodic functional approach to the calculus of variations and the problem of time-dependent damped harmonic oscillators ［J］.Appl Math Lett，2011，24:1647－1653.

［10］梅凤翔.李群和李代数对约束力学系统的应用［M］.北京:科学出版社，1999.

［11］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.

［12］LUO S K，CAI J L，JIA L Q.Noether symmetry can lead to non-Noether conserved quantity of holonomic nonconservative systems in general Lie transformations［J］.Commun Theor Phys，2005，43(2):193－196.

［13］张毅.非完整力学系统的Hamilton对称性［J］.中国科学:物理学 力学 天文学，2010，40:1130－1137.

［14］贾利群，郑世旺，张耀宇.事件空间中非Chetaev型非完整系统的Mei对称性与Mei守恒量［J］.物理学报，2007，56(10):5575－5579.

［15］WU H B，MEI F X.Symmetry of lagrangians of holonomic systems in terms of quasi-coordinates［J］.Chin Phys B，2009，18(8):3145－3149.

［16］龙梓轩，张毅.Birkhoff系统Lie对称性逆问题的两种提法和解法［J］.华东师范大学学报:自然科学版，2012(3):49－55.

［17］ZHANG Y，ZHOU Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems［J］.Nonlinear Dynamics，2013，73(1/2):783－793.

［18］LONG Z X，ZHANG Y.Noether's theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space［C］∥Acta Mechanica，2013，DOI 10.1007/s00707 －013 －0956 －5.

［19］张毅.相空间中类分数阶变分问题的Noether对称性与守恒量［J］.中山大学学报:自然科学版，2013，52(4):45－50.