基于边界元法的特高压杆塔接地体电流密度计算

周 玮 王 兵

（河海大学能源与电气学院，江苏南京 210098）

“十二五”期间，我国在特高压交流试验示范工程基础上，结合大水电、大煤电、大风电基地接入系统的需要，计划重点加快华北、华东、华中特高压交流电网建设。到2015“三华”特高压电网形成“三纵三横”主网架，特高压输电工程建设将进入快速发展通道。随着国家经济的迅速发展，电网的安全性稳定性显得更为重要。特高压杆塔良好的接地是电力系统安全、稳定的重要条件。入地电流在通过特高压杆塔接地极散流时，会出现导体电流密度分布不均匀，由于电流密度分布不均容易导致接地极电流密度大处产生更多的热量从而引起接地极的局部过热，进而使得接地极过热处较容易腐蚀。接地极的腐蚀又反过来使得电流密度分布不均匀问题更加突出，两者互相促进，最后影响接地极的散流。此外，接地极电流密度分布不均也会影响接地接安全，如500kV葛上线南桥换流站接地极曾今由于电流分布不均导致接地极和引流电缆被烧毁。因此，计算特高压杆塔接地极上的电流密度分布，对特高压输电工程的建设有重要意义。

工程上以假设接地极电流密度平均分布为基础，用中点电位法或平均电位法得出接地极电阻的解析公式。该方法存在一定误差且无法求得接地极电流密度的分布情况。目前计算接地极上的电流密度分布的方法，主要有边界元法和有限元法。

本文应用边界元法来计算特高压杆塔自然接地极电流密度分布，并采用不同的插值方法，通过比较分析，给出了更符合实际情况的电流密度分布及最大电流密度点，计算分析了典型特高压杆塔自然接地极的电流密度分布，为实际工程建设提供一定的借鉴和参考。

1 边界元计算方法

边界元法是把边值问题等价地转化成边界积分问题，对于边界积分的求解，边界元法是一种有效的数值计算方法，基本思路是：边界元法将区域的边界分割成n个边界单元，整个边界上的积分以n个边界元上的积分和来表示。各边界单元上的函数值和函数的法向导数值，可以通过插值函数和边界单元上有限个点的函数和函数的法向量，以多项式近似。

对于设有有一恒定电流I流入埋设在电阻率为ρ的均匀土壤中的电极，在周围空间任意一点 ),,( zyxP 处的电位u满足拉普拉斯方程为：

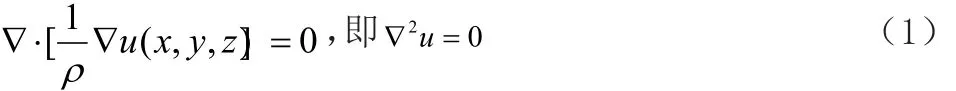
其边界条件为：

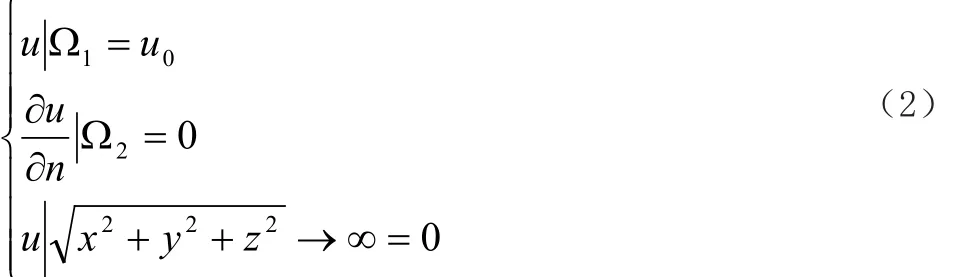
式中：1Ω为接地极边界，2Ω为地面边界，n为法向向量。

考虑土壤结构为均匀土壤时，采用半无限域中拉普拉斯方程的基本解：

式中：R为源点到场点的距离，R’为源点的镜像到场点的距离。

由于接地极一般细长，因此在进行接地极的电场计算时，可认为电流集中有接地体轴线出流出，如图1所示垂直接地体，若已知接地体线电流密度分布函数δ(x',y',z')，则地中任意一点P ( x ,y,z)的电位为

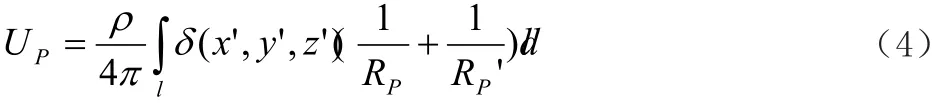
接地体表面任意一点 ),,( zyxB 的电位为：

当把接地体剖分为N段，在求解上述积分方程时，应用边界元法基本原理，可以得到一组解线电流密度jδ的联立代数方程：

式中Aij为电位计算系数，表示由线电流密度δj所决定的匹配点i的电位。在计算中，采用不同的边界元插值法得到不同的电流密度分布，电流密度沿边界元的分布可以为均匀的（边界元零次插值法），线性的（边界元线性插值法），以致高次曲线型的（边界元多次插值法），显然电位计算系数会随着线电流密度的改变而不同。由于接地体是等电位的，所以 U1= U2… = UN=U0，假设已知注入接地体的电流I，根据文献[4]可求得电位系数 A ij，则可由式（6）求出δ1,δ2…δN及 U0，从而得到接地体电流密度分布及接地电阻 R = U0I。

对于特高压杆塔基础自然接地极电流密度计算，本文采用边界元零次插值法和一次插值法，零次插值就是把接地体分成有限个小单元，每一小单元段的电流密度为常数；一次插值意味着电流密度在小单元内线性分布。应用边界法计算特高压杆塔接地电流密度的算法流程图如图2所示。

2 应用分析

2.1 程序验证

典型特高压杆塔自然接地极的基本参数：接地体半径为0.44m，长度为30m，埋深为零。土壤结构为均匀土壤，土壤电阻率为100欧米。注入电流为10A。本文用C语言编程计算特高压杆塔自然接地极三种不同分段方式下电流密度分布及接地电阻，并与CDEGS软件计算的电流密度分布及接地电阻进行了比较，结果如表1，表2，表3所示，表中的边界元法计算结果为零次插值的结果。从三个表中可以看出，无论采用比例分段方式，还是采用均匀分段方式，边界元法的电流密度分布及接地电阻计算结果与CDE GS软件的计算结果是吻合的。

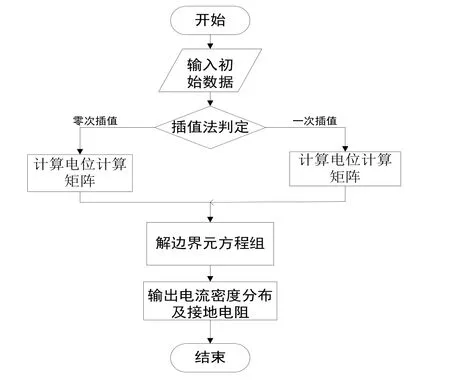
图2 边界元法流程图

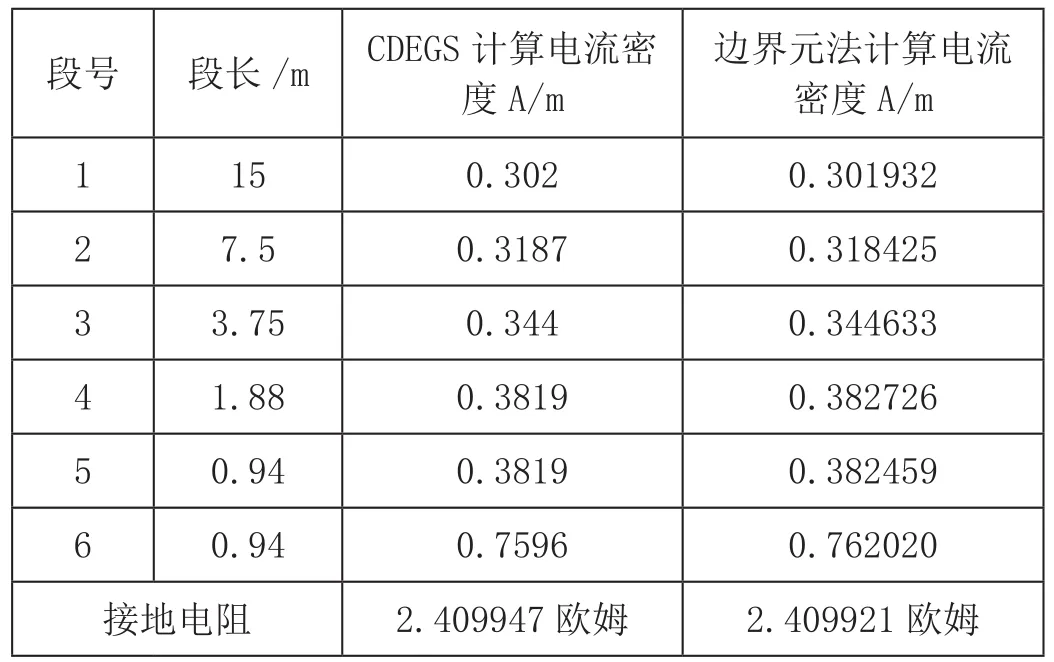
表1 分段方式一下电流密度分布及接地电阻

表2 分段方式二下电流密度分布及接地电阻

2.2 零次插值法与一次插值法比较

在边界元法计算中，采用不用的插值方法，得到的电流密度分布是不同。本文对特高压杆塔的自然接地极电流密度分布计算，采用了零次插值和一次插值两种方法。典型特高压杆塔自然接地极的基本参数：接地体半径为0.44m，长度为30m，埋深为零。土壤结构为均匀土壤，土壤电阻率为100欧米。注入电流为10A。若接地极采用比例分段方式，将特高压杆塔分为6段，其沿接地体电流密度分布如图3。两种方法的电流密度都是从地面往逐渐增大，地面处接地体端点的电流密度最小，接地体末端点电流密度最大，但是采用一次插值得到的最大电流密度比零次插值的最大电流密度大很多。

若用采用均匀分段方式把特高压杆塔自然接地极分成30段，采用零次插值法和一次插值法两种计算方法下的电流密度分布，如图4所示。从图中可以看出，两种插值方法下电流密度分布趋势是相同的，但是一次插值法的最大电流密度要比零次插值法的电流密度大。

从而，在计算特高压杆塔自然接地极的最大电流密度值时，采用一次插值方法计算更好，且一次插值计算的电流密度分布更符合实际当中的电流密度分布。

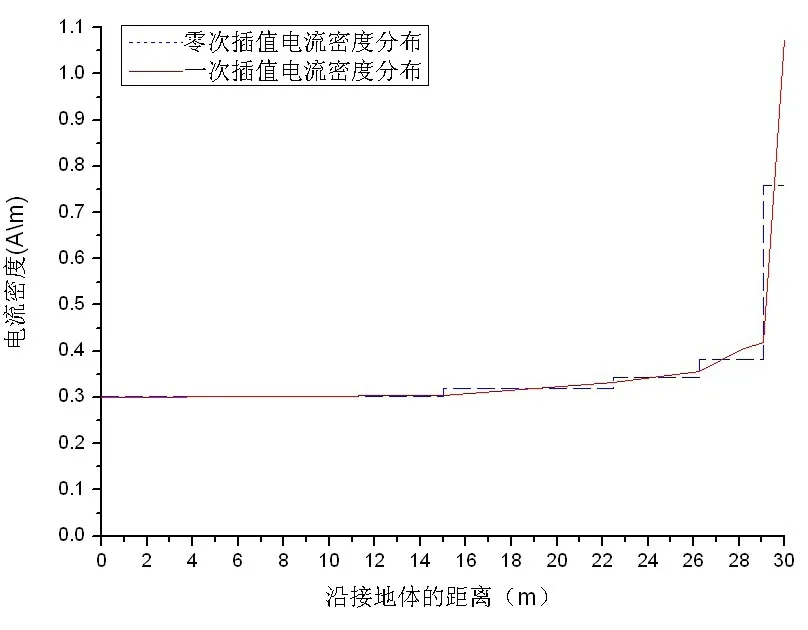
图3 比例分段的电流密度分布

图4 平均分段的电流密度分布

3 结论

3.1 本文采用边界元法对特高压杆塔基础自然接地极的电流密度进行计算，并用本文计算结果与权威接地计算软件CDEGS计算结果进行了比较，结果相吻合，从而验证了方法的正确性；

3.2 本文用边界元法计算特高压杆塔电流密度时，采用零次插值和一次插值两种方法，通过对比分析了两种方法的计算结果可知，一次插值法更能精确的表示电流密度沿特高压杆塔基础分布。

[1] 李晓丽.变电站接地网冲击特性研究[D].重庆:重庆大学硕士学位论文，2008.

[2] 袁涛,司马文霞,李晓莉.两种常见接地极电流分布的探讨[J].高电压技术，2008，34(2)：239-242.

[3] 鲁志伟,史艳玲,文习山.垂直分层土壤中接地电阻的测量及其误差分析[J].高电压技术,2001,27(3):36-37.

[4] 解广润. 电力系统接地技术[M] . 北京:水利电力出版社,1991.

[5] 阮江军.直线型直流接地极附近二维电流场边界元法计算[J].高电压技术,1997,23(3):49-50,74．

[6] 杜忠东，王建斌，刘熙.UHVDC圆环接地极接地性能分析[J].高电压技术，2006,32(12):146-149.

[7] Zhong-Xin Li*,Guang-Fan Li,Jian-Bin Fan and Cui-Xia Zhang.Numerical calculation of grounding system buried in vertical earth model in low frequency domain based on the boundary element method[J]. European Transaction on Electrical Power,2009,19(8): 1177-1190.

[8] 陈媛，文习山.有限元法计算地中交流电流分布[J].高电压技术，2006，32(4)：98-100.

[9] 陈水明, 施广德, 赵智大. 直线型直流接地极电流场分析[J].高电压技术,1994,20(3):8-13.

[10] 陈慈萱. 地网的热稳定和流散电流分布[ J ] . 高电压技术. 1987 ,12 (2) : 33-38．

[11] 杨德全. 赵忠生. 边界元法理论及其应用[M]. 北京：北京理工大学出版社.2002:1-109.

[12] 张曾，文习山.任意块状结构土壤中接地的边界元法分析[J].高电压技术，2010,34(9):170-174.

[13] 厉天威，何民等.输电线路杆塔接地电阻的简化计算[J].电网技术，2011,35(9):170-175.

[14] Zhong-Xin Li*, and Jian-Bin Fan. Numerical calculation of grounding system in low frequency domain based on the boundary element method[J].International Journal for Numerial Methods in Engineering 2008; 73:685-705.

[15] Colominas I, Navarrina F, Casteleiro M.A numerical formula for grounding system analysis in stratified soils.IEEE Transactions on Power Delivery 2002;PWRD-17:587-595.

[16] 曹晓斌，胡劲松，余波等.一类垂直双层土壤中地网接地电阻的简易计算公式[J].中国电机工程学报，2009，29(1):120-125.

[17] 苏杰，吴广宁，周炜明等.异质土壤对地网接地电阻的影响[J].电网技术，2010，34(9)：166-169.