矿用减速器行星架结构探讨

张小峰

（中国煤炭科工集团 太原研究院，山西 太原 030006）

0 引言

行星传动以功率体积比大的优点广泛应用于各类减速器，行星传动主要构件有太阳轮、行星轮、内齿圈、行星架等。行星架为行星传动的主要构件，承受外力矩最大，其结构形式和制造质量对行星轮间载荷分配及传动装置承载能力、噪音和振动等有很大影响。合理的行星架结构应该质量轻、刚性好、便于加工和装配。目前，常见的行星架结构形式有双壁整体式、双壁剖分式和单壁式，本文主要对矿用NGW 型双壁整体式行星架的结构进行探讨，双壁整体式行星架刚性好，受载后变形较小，有利于行星轮上载荷均匀分布，有效减小振动和噪声。

1 结构形式

NGW 型双壁整体式行星架由两侧壁通过中间连接梁连接在一起，调研结果表明，目前国内矿用NGW 型行星架常用图1所示的四种结构，图1（a）属于基本结构， 广泛应用于各种行星减速装置， 图 1（b）、（c）、（d）为不同制造商的优化结构。比较各结构可见，四种行星架两侧壁及输出部分结构基本一致， 图（b）、（c）、（d）三种行星架优化点均在连接梁结构。

2 结构分析

本文选用一型矿用运输减速器行星架为蓝本，按图1所示的四种不同的结构建立三维实体模型进行分析。减速器行星级输入功率P0=45 kW，输入转速n0=1453 r/min，输入扭矩T0=295.8N·m， 太阳轮/行星轮/内齿圈齿数分别为19/22/65，模数为3mm，中心距64 mm，行星轮数目为3，行星架输出。

图1 矿用NGW 型行星架结构

2.1 行星架受力分析

行星架受力源自行星轮，不考虑均载系数情况下：Ftac=Ftbc=1000Ta/Csra=1000×295.8/（3×28.5）≈3456N其中： Ta—太阳轮传递的转矩（N·m）；Cs—行星轮数目；ra—太阳轮的分度圆半径，本例28.5mm；Ftac—太阳轮给行星轮的切向力；Ftbc—内齿圈给行星轮的切向力。

行星架受力点为两侧壁承载轴承安装孔，行星架受力点与行星轮中性面距离相等则有：

切向方向： RH左=RH右=Ftac=Ftbc=3456 N。

径向方向：太阳轮给行星轮的径向力Frac与内齿圈给行星轮的径向力Frbc等值反向，合力为零，则有RV左=RV右=0。

2.2 行星架有限元分析

本文采用有限元法对不同行星架进行分析，直观反映行星架受力后应力以及变形情况。行星架的材料统一选用ZG310-570，该材料屈服极限σs=310Mpa，弹性模量： E=2.0×1011Pa， 泊松比： 0.3， 密度： 7800kg／m3。

简化模型输出部分为圆柱孔，对该处施加切向、径向以及轴向零位移约束，分别在两侧壁三对承载孔上按余弦函数分布方式施加面应力载荷，载荷按照恶劣工况施加，载荷系数取2.0，偏载系数取1.5。施加约束和载荷后的行星架部件有限元分析应力和变形结果如图2～图5所示。

图2 结构a 应力和变形云图

图3 结构b 应力和变形云图

图4 结构c 应力和变形云图

图5 结构d 应力和变形云图

2.3 行星架结构比较

云图表明，虽然结构不同，但各行星架最大应力值和综合位移值位置基本一致。表1 列出四种结构的质量、最大应力值和最大综合位移值,分析数据可得，即使在极限工况下，该行星架的安全系数也较高。以结构a为基准，计算偏差值，计算方法为：

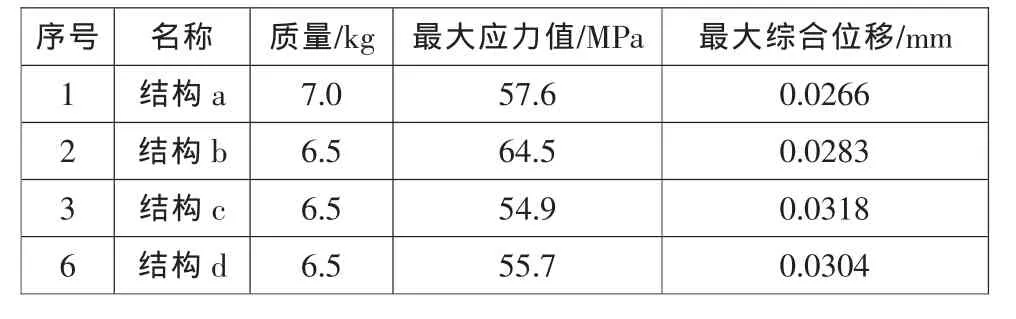
表1 四种结构质量、最大应力及位移值

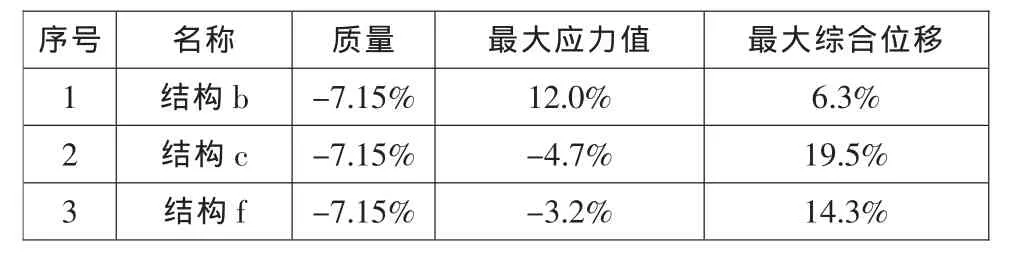
表2 b、c、d 结构相对于a 结构偏差

式中：X为b、c、d。表2为各结构相对于结构a的偏差值。

综合分析上述内容可得，结构b 和结构d 属于优化较好的结构。结构b 虽然最大应力值增加了12%，但壁厚均匀，便于铸造，且该结构应力值分布均匀；结构d最大应力值减小3.2%，虽然综合位移值增加14.3%，但结构简单，连接梁处大量采用直线段，可以采用多种手段加工，该结构特别适合锻造行星架的加工。

3 结束语

一般矿用行星架安全系数较高，因此，行星架结构优化主要方向为提高结构的整体刚度、减轻结构重量和优化行星架的加工工艺性。

[1]饶振钢.行星齿轮传动设计[M].北京：化学工业出版社，2003.

[2]华剑，周思柱，李超.基于SolidWorks的行星架有限元分析及优化设计[J].煤矿机械，2011，2.

[3]蒋仁科，林腾蛟，荣崎.同轴双输出行星齿轮减速器结构优化设计[J].机械研究与应用，2008，2.