摄像机标定及矫正技术研究

马鸿飞，苗振海，陈妍言，贺志强，魏 淼

（1.机科发展科技股份有限公司，北京 100044；2.北京机床研究所，北京 100102）

0 引言

机器视觉也称为计算机视觉，是一种研究用计算机来模拟生物视觉功能的科学和技术，它是计算机科学、自动化技术、人工智能技术、模式识别和光学等学科的综合。机器视觉的基本任务之一是从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体。而空间物体表面某点的三维位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数，通过实验与计算得到这些参数的过程就叫摄像机标定。标定精度的高低，直接影响着机器视觉系统的精度。所以，在标定过程中，高刻画精度的标定模板和与之相匹配的标定算法是保证标定精度的必要条件。由于相关标定算法的研究已很多，本文在论述了摄像机标定原理和模型后，重点通过Halcon 视觉处理软件实验分析论证摄像机标定图像数量对标定精度的影响，以及通过对游标卡尺的图像处理，来对比分析矫正图像前后的区别。

1 摄像机标定原理及实现

在实际应用中，一般应用面阵摄像机标定，它的针孔摄像机模型如图1所示。其中，图像坐标系（r，c），成像平面坐标系（u，v），摄像机坐标系（x，y，z），世界坐标系（xw，yw，zw）， Sx，Sy是缩放比例因子， 它们表示图像传感器上水平和垂直方向上相邻像素之间的距离。f 表示的并不是镜头的焦距，而是摄像机主距。点P 是世界坐标系中点Pw在成像平面上的投影。

世界坐标系中的点 Pw=（xw，yw，zw）T变换到它在成像平面坐标系上的投影点P，需要经历以下四个步骤：

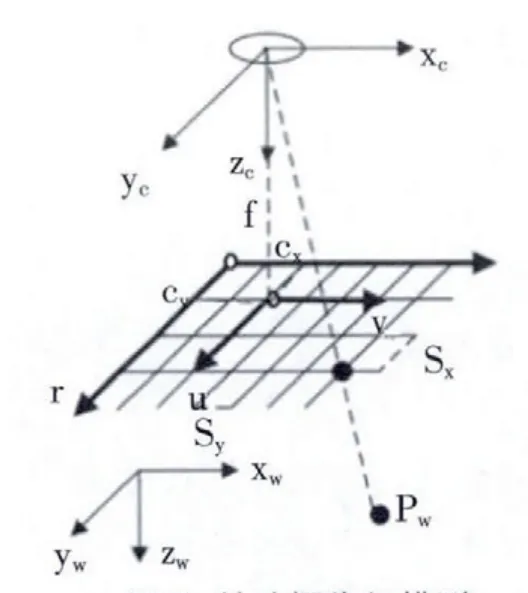
图1 针孔摄像机模型Fig.1 The pinhole camera model distortion

（1）点 Pw=（xw,yw，zw）T变换到摄像机坐标系中的点 P=（x，y，z）T， 关 系 为 Pc=RPw+T。 T=（tx，ty，tz）T是一个平移向量，R=（α，β，γ）是一个旋转矩阵，α，β，γ 是分别绕摄像机坐标系 x，y，z轴的旋转角度。在R和T中6个 参 数（α，β，γ，tx，ty，tz）称为摄像机外参，它们决定了摄像机坐标系与世界坐标系之间的相对位置。

（2）摄像机坐标系中点Pc变换到成像平面坐标系，它们之间是透视投影关系：

（3）在不考虑镜头畸变的情况下，世界坐标系中的点Pw与成像平面中的投影点P之间的直线过摄像机光学中心。大部分情况下，镜头的畸变可以近似为径向畸变，即：

式中：参数k决定了径向畸变的程度，k＞0为枕形畸变，k＜0为桶形畸变。

式中：（Cx，Cy）T是光心在成像坐标系中的投影点。由以上可知，摄像机标定的实质就是确定内部参数（f，k，Cx，Cy，Sx，Sy）和外部参数（α，β，γ，tx，ty，tz）的过程。

在Halcon软件中主要使用了read_image，find_caltab，find_marks_and_pose， camera_calibration， write_cam_par等算子来获得摄像机标定的内外参数。

2 标定图像次数对其内外参数的影响

为了分析标定图像次数对内外参数的影响，实验中将标定板放置于视野不同位置进行多次标定，经过实验所得结果如图所示，主要使用calibrate_cameras()，get_calib_data()两个算子。

放置过程中，标定板移动既有平行也有旋转。处理结果如图2～5所示。图中横坐标为图像的张数，纵坐标分别为主距F、畸变系数K、缩放因子Sx，光心 Cy的真实值和标准差，可以看到随着图片张数的增加，其标准差越来越小，最终趋于稳定。所以为了使得到摄像机参数的更加准确，就需要有相当多的标定图像。标定板在标定图像中最好能覆盖整个视野并尽可能覆盖摄像机外参的范围，当标定板在标定图像中覆盖每个角落，可以计算得到更准确的畸变系数K，当其可以覆盖较大的深度范围时所有摄像机参数都会更准确。因此进行标定摄像机的图像数量和位置是影响摄像机参数准确度不能忽视的因素。

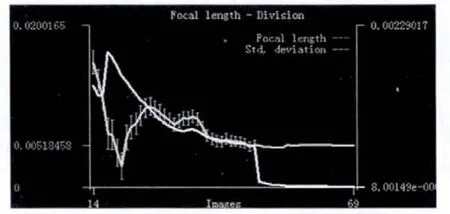
图2 主距F随着标定图像增加趋于准确Fig.2 Principal distance is more accurate

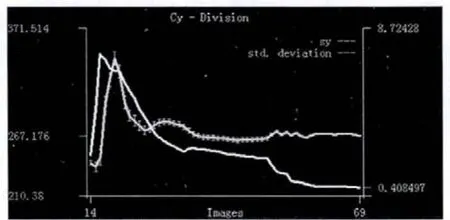
图3 畸变系数K随标定图像增加趋于准确Fig.3 Deformation cofficient is more accurate

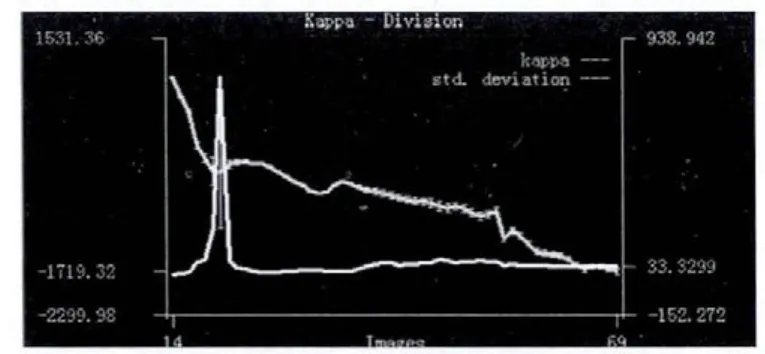
图4 缩放因子Sx随标定图像增加趋于准确Fig.4 Scale factor is more accurate

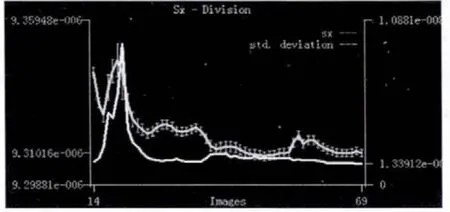
图5 光心Cy随标定图像增加趋于准确Fig.5 Optical center is more accurate

3 摄像机矫正技术的研究

在精确测量和定位中，一般需要通过标定后的参数对原始图像进行矫正，以防止镜头畸变和相机安装倾斜造成的误差，为很好的验证摄像机标定及矫正的必要性，利用游标卡尺进行了相关验证。实验中所用的相机为30万像素，像元大小为7μm，镜头为畸变数K 约为-734的普通镜头，将相机与镜头固定调节至较好位置，将游标卡尺放置于平面内，将标定板平放于游标卡尺一端进行标定后，接着单独采集到游标卡尺图像如图6所示。采用图7 处理流程来计算刻度线的平均宽度，最终结果如图8。从处理结果可以得到两个刻度线的平均距离为0.78945mm，最小误差为17μm，最大误差为25μm。造成如此大的误差的原因主要有两个：一是镜头的畸变，使得成像中不同区域的刻度线宽度不同。二是摄像头安装角度偏移3 度造成，这样摄像机采集的图像就有会出现离镜头相对近的地方两刻度线的像素数较少，离镜头相对较远的地方两刻度线内的像素较多，而标定板获得的像元大小是在离镜头较近处进行标定获得的，使得最终误差相对标准值1mm 有较大的距离。经过摄像机标定后的内外参数来矫正图形后处理结果如图9所示，可获得刻度线的平均长度为0.99mm，其最大误差在10μm。这是因为通过矫正和转换得到的图像相当于摄像机在与世界平面绝对垂直并且镜头基本不存在畸变的情况下拍摄的图像，使图像中所有像素在世界坐标中所代表的实际大小与真实相符。所以从实验可知，在进行高精度测量定位以及模板匹配时需要进行摄像机标定及矫正图像。

图6 游标卡尺图像Fig.6 Vernier caliper image

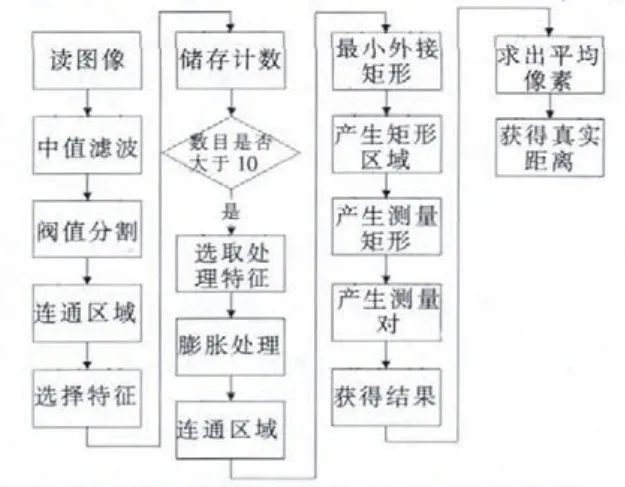
图7 刻度线平均宽度图像处理流程图Fig.7 The image processing flow chart of the average width of Scale line

图8 未矫正前处理结果Fig.8 The processing results without correction

图9 矫正后处理结果Fig.9 The processing results with correction

4 总结

摄像机标定建立了图像坐标系和世界坐标的关系，是机器视觉理论研究的热点之一，本文在对摄像机原理进行论述后，结合了摄像机标定参数准确性研究和摄像机矫正技术的研究，对摄像机不同位置标定次数对精度的影响进行了相关论述和验证，得出了多次不同位置的标定可以提高摄像机内外参数准确性的结论；选用了游标卡尺作为摄像机矫正前后的参考，得出了为保证精度，在使用普通镜头时进行高精度测量和匹配时必须进行摄像机标定和矫正图像的结论。所得结论为以后的工程应用提供了较好的依据。

[1]苗振海，等.基于Halcon的FPC 不规则贴胶片的视觉定位算法研究与开发[J].制造业自动化，2013，1.

[2]Milan Sonka,VaclavHlavac,Roger Boyle.图像处理分析与机器视觉[M].清华大学出版社，2011.

[3]张铮，等.数字图像处理与机器视觉—Vc++与Matlab 实现[M].人民邮电出版社，2011.

[4]Carsten Steger,Markus Ulrich.机器视觉算法与应用[M].清华大学出版社，2008.

[5]罗珍茜，薛雷，等.基于HALCON的摄像机标定[J].视频应用与工程，2010，5.