层状复合材料矩形截面非圆柱螺旋弹簧的自由振动

郝 颖，虞爱民

（同济大学航空航天与力学学院，上海 200092）

引 言

非圆柱螺旋弹簧的特性线具有很强的非线性，能够适用于多种受限制的安装空间，在工程实际中有着广泛的应用［1～3］。簧丝截面为非圆形的非圆柱螺旋弹簧，具有蓄存能量大、有效平缓应力分布、压并高度低，压缩量大等优良性能［4］，被广泛用于发动机阀门、离合器和自动变速等装置上。

由于复合材料具有强度高、耐腐蚀、电绝缘性好、比重小和设计性强等诸多优点，在工程实际中逐渐开始使用复合材料来制备弹簧。但目前复合材料在弹簧制造领域的应用还非常有限，现有的尝试多是用来加工板簧，对于应用范围最广的螺旋弹簧的研发很少［5］，而对于设计性较强的层状复合材料的非圆柱螺旋弹簧的研究则更为罕见。据作者所知，只有极少的文献［6～8］涉及到此类问题。1999年Yildirm首次导出了各向异性材料空间曲杆的运动微分方程［6］，之后Yildirm又以传递矩阵法对层状复合材料非圆柱螺旋弹簧的自由振动问题进行了系统的分析［7，8］。在上述研究中虽然考虑了转动惯量、轴向和剪切变形的影响，然而所涉及的曲杆和弹簧的横截面均为圆形，因而无从考虑翘曲变形对振动特性的影响。文献［9，10］已经研究了各向同性材料非圆截面圆柱螺旋弹簧的自由振动问题。计算表明，即使对于此类弹簧，翘曲变形对固有频率也有着重大的影响，在动力分析中必须加以考虑。鉴于目前对层状复合材料非圆截面非圆柱螺旋弹簧理论研究工作的缺乏和均未考虑翘曲效应的情况，本文首先建立了包括翘曲效应的各向异性自然弯扭梁理论，在此基础上，导出了对称层状复合材料矩形截面非圆柱螺旋弹簧的运动微分方程，它们由14个变系数的一阶偏微分方程组成。此外，根据文献［11］的翘曲模式可以导出层状复合材料矩形截面杆件的扭转翘曲函数。在增加了广义翘曲坐标和广义翘曲力矩两个自由度后，方程呈现出很强的刚性，这里采用文献［12，13］中改进的Riccati传递矩阵法对弹簧的运动微分方程进行求解。本文拟解决弹簧的固有频率与翘曲效应及其几何参数之间的关系。

1 考虑翘曲效应的各向异性自然弯扭梁理论

1．1 自然弯扭梁的几何关系

设各向异性自然弯扭梁横截面形心的轨迹是一根连续的空间曲线，曲线l的切线、主法线和次法线单位矢量分别用t，n，b表示。为了考虑梁的初始扭曲，引入直角坐标系x1ξη为横截面的形心主轴，如图1所示。x1轴与曲线的切线t重合，ξ轴与曲线主法线n之间的夹角记为θ，它通常是弧坐标s的函数。用iξ和iη表示O1ξ和O1η方向的单位矢量，则［14］

式中 上标撇号表示对弧坐标s的微分。kξ＝k1sinθ，kη＝k1cosθ，ks＝k2＋θ′，k1，k2分别为曲线的曲率和扭率。

图1 各向异性自然弯扭梁的几何关系Fig．1 Geometry of naturally curved and twisted anisotropic beams

1．2 弹性矩阵的坐标变换与本构方程

线弹性复合材料的广义胡克定律为［15］

这里

式中σs，σξ，ση，τξη，τsη和τsξ分别为杆件内任意一点的3个正应力和3个切应力；ess，eξξ和eηη分别为相应方向的线应变；2eξη，2esη和2esξ分别为该点在3个坐标平面内的工程切应变。假设与单向复合材料轴向一致的坐标系123绕3轴在12面内转过了ψ角，到达另一个新的坐标系xyz（如图2所示），根据经典层合板理论［15］，即可确定在新的坐标系下刚度矩阵C′及柔度矩阵S′中的每一个元素。同时可以得到在新的坐标系下应力与应变的关系为

式中 折减刚度系数Q′ij的表达式参见文献［6］。经计算可得，对于0°及90°铺层的层合板，有

图2 铺层的结构坐标轴x，y，z和材料主轴（1，2，3）之间的关系Fig．2 Relation between structural axes （x，y，z）and principal material axes（1，2，3）for a single ply

式中T定义为广义翘曲力矩；εs，εξ和εη为杆轴上一点沿3个坐标方向的线应变；ωs，ωξ和ωη为杆轴单位长度的3个相对转角；φ为圣维南扭转翘曲函数；α为广义翘曲坐标。这里用A（k），Q′（k）ij和φ（k）分别表示层状复合材料各铺层的截面面积、折减刚度系数和翘曲函数，对i＝1，5，6，有

如果在式（5）中代入线应变和相对转角的表达式［13］，则可以得到用6个位移函数us（s，t），uξ（s，t），uη（s，t），φs（s，t），φξ（s，t），φη（s，t）和α（s，t）表示的本构方程。

1．3 运动微分方程

自然弯扭梁在考虑翘曲效应情况下的运动微分方程可以改写为［14］

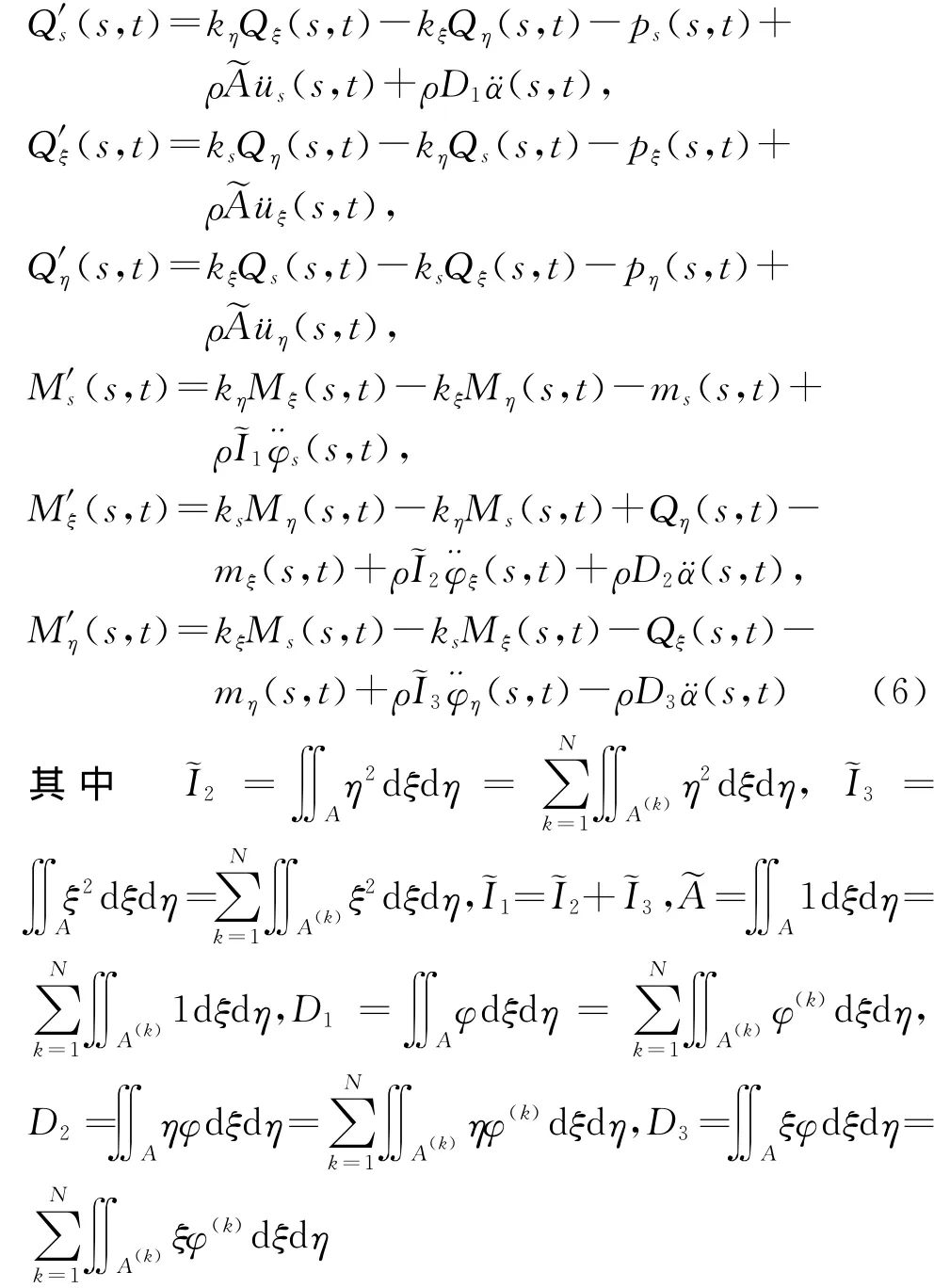
式中 上标圆点表示对时间t的微分。广义翘曲力矩T（s，t）对弧坐标s的一阶导数则为

对i＝1，5，6，有

把式（5）代入式（6），然后把其中的线应变和相对转角以及式（7）中的轴向应力、线应变和相对转角用6个位移函数和广义翘曲坐标代入，即可得到各向异性自然弯扭梁用位移函数和广义翘曲坐标表示的运动微分方程，它们由7个变系数的二阶（关于弧坐标s）偏微分方程组成。

1．4 对称层状复合材料矩形截面杆件的扭转翘曲函数

注意到上述方程中有许多对翘曲函数求导或者求积分的项，为了考虑横截面的翘曲变形对非圆柱螺旋弹簧固有频率的影响，必须得到层状复合材料矩形截面杆件翘曲函数的显式表达式。设对称铺设［0°／90°／90°／0°］的复合材料矩形截面杆件如图3所示。

图3 对称铺设［0°／90°／90°／0°］的复合材料矩形截面杆件Fig．3 Symmetrical laminated［0°／90°／90°／0°］composite bars with rectangular cross－section

式中

2 对称层状复合材料矩形截面非圆柱螺旋弹簧的运动微分方程

如图4所示，非圆柱螺旋线是一条变曲率、变扭率的空间不规则曲线，其几何关系为

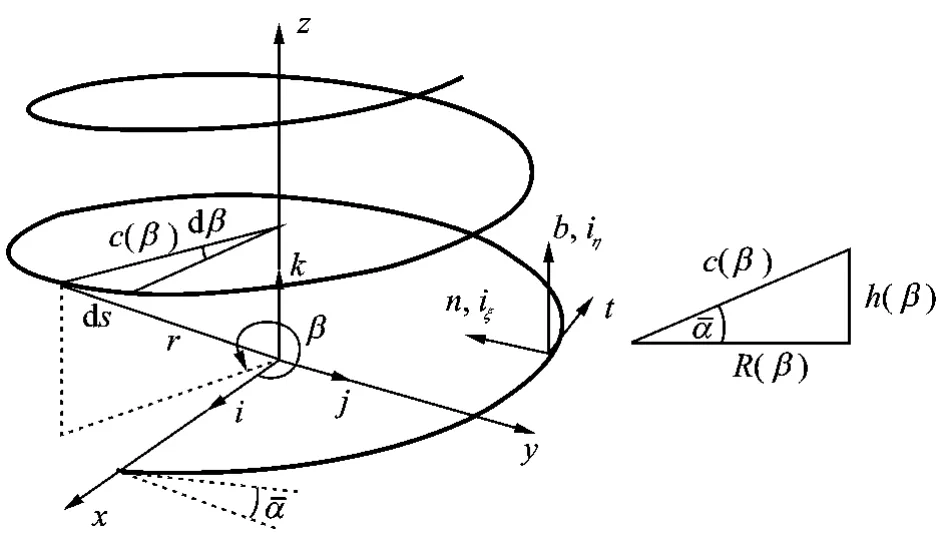
图4 非圆柱螺旋线的几何性质Fig．4 Geometry of a typical non－cylindrical helix

其中α为螺旋角，R（β）和h（β）分别表示螺旋线的中径和节距，它们皆为水平角β的函数。ks（β）＝h（β）／c2（β），kη（β）＝R（β）／c2（β）分别表示螺旋线的曲率和扭率。如果以n表示弹簧的有效圈数，则锥形弹簧螺旋线上任意点的中径为（见图5）

双曲形和桶形弹簧螺旋线上任意点的中径为

把式（5）和（7）中的线应变和相对转角用6个位移函数和广义翘曲坐标代入，然后对式（5）进行联立求解，可以得到各位移函数和广义翘曲坐标关于弧坐标s一阶导数的表达式，再利用这个结果来消去式（7）中有关位移函数和广义翘曲坐标的一阶导数，最后把这些方程和式（6）进行组合即可得到用位移函数、内力分量、广义翘曲坐标和广义翘曲力矩一阶导数表示的层状复合材料非圆截面非圆柱螺旋弹簧的运动微分方程，它们由14个变系数的一阶（关于弧坐标s）偏微分方程组成。如果不考虑杆件的初始扭曲（kξ＝0），并令ps＝pξ＝pη＝ms＝mξ＝mη＝0，假设对称层压复合材料矩形截面非圆柱螺旋弹簧作频率为ω的简谐运动，利用ds＝cdβ，注意到与矩形截面翘曲函数φ（ξ，η）有关的积分D1，D2，D3和Dii01，Dii02，…，Dii17中有许多等于零，则可以得到该弹簧的自由振动微分方程为

图5 不同类型的非圆柱螺旋弹簧Fig．5 Different types of non－cylindrical helical springs

在增加了广义翘曲坐标和广义翘曲力矩两个自由度后，方程呈现出很强的刚性，本文采用文献［12，13，16］中改进的Riccati传递矩阵法对上述微分方程组进行求解。

3 数值算例

设两端固支对称铺设［0°／90°／90°／0°］的复合材料非圆柱螺旋弹簧的材料（T300／N5208）和几何性质分别为：E1＝181GPa，E2＝E3＝10．3GPa，G12＝G13＝7．17GPa，G23＝3．433GPa，μ12＝0．28，ρ＝1 600 kg／m3。矩形截面沿ξ方向的边长用2a表示，沿η方向的边长用2b表示。螺旋线的最大、最小半径R1，R2（如图5所示），有效圈数n，螺旋角α，剪切形状因子Gξ＝Gη＝0．842，扭转翘曲函数如式（8）所示。

3．1 算例1

取R1＝10mm，R2＝6mm，α＝5°，n＝4，2a＝1mm，2b＝0．8mm。在对3种不同形状的对称层压复合材料矩形截面螺旋弹簧进行有限元分析时，均将其划分为720个Solid46实体层合单元，其中沿螺旋线均分为360份，总节点数为2 166个。表1～3综合了这3种不同形状的弹簧分别在考虑与忽略翘曲影响得到的计算结果和ANSYS的结果。

3．2 算例2

取α＝5°，n＝4，2a＝1mm，2b＝0．8mm，表4表示了不同的最大最小半径比R2／R1对对称层压复合材料矩形截面双曲形弹簧固有频率的影响。

表1 对称层压复合材料矩形截面锥形弹簧的前5阶频率Tab．1 The first five frequencies of symmetrical laminated composite conical－type springs with rectangular crosssection

表2 对称层压复合材料矩形截面双曲形弹簧的前5阶频率Tab．2 The first five frequencies of symmetrical laminated composite hyperboloidal－type springs with rectangular cross－section

表3 对称层压复合材料矩形截面桶形弹簧的前5阶频率Tab．3 The first five frequencies of symmetrical laminated composite barrel－type springs with rectangular crosssection

表4 R2／R1对对称层压复合材料矩形截面双曲形弹簧固有频率的影响Tab．4 The effect of（R2／R1）on frequencies of symmetrical laminated composite hyperboloidal－type springs with rectangular cross－section

3．3 算例3

取R1＝10mm，R2＝6mm，n＝4，2a＝1mm，2b＝0．8mm，表5表示了不同的螺旋角对对称层压复合材料矩形截面双曲形弹簧固有频率的影响。

表5 螺旋角对对称层压复合材料矩形截面双曲形弹簧固有频率的影响Tab．5 The effect of helix pitch angle）on frequencies of symmetrical laminated composite hyperboloidal－type springs with rectangular cross－section

表5 螺旋角对对称层压复合材料矩形截面双曲形弹簧固有频率的影响Tab．5 The effect of helix pitch angle）on frequencies of symmetrical laminated composite hyperboloidal－type springs with rectangular cross－section

1阶 2阶 3阶 4阶 5阶有限元α＝4° 本文解 223．83 485．16 580．38 600．77 777．21有限元214．72 471．92 563．13 595．93 784．06α＝5° 本文解 222．11 489．36 561．03 576．27 795．05有限元213．70 471．27 543．66 563．67 794．83213．25 468．11 524．99 533．38 782．43α＝6° 本文解 221．32 487．63 540．08 549．27 797．11有限元211．67 436．45 474．64 492．73 745．06α＝8° 本文解 219．45 462．32 495．34 510．20 782．86 α＝10°有限元 208．41 383．72 429．34 479．23 691．23本文解216．67 414．81 453．53 495．81 754．33

3．4 算例4

取R1＝10mm，R2＝6mm＝5°，2a＝1mm，2b＝0．8mm，表6表示了不同的有效圈数n对对称层压复合材料矩形截面双曲形弹簧固有频率的影响。

表6 有效圈数n对对称层压复合材料矩形截面双曲形弹簧固有频率的影响Tab．6 The effect of helix coil number（n）on frequencies of symmetrical laminated composite hyperboloidal－type springs with rectangular cross－section

4 结 论

本文首次在层状复合材料矩形截面非圆柱螺旋弹簧的运动微分方程中考虑了翘曲变形的影响。从表1～3可以看出，翘曲变形对该弹簧的固有频率具有重大的影响，在自由振动分析中必须加以考虑。不考虑翘曲变形时，计算所得前5阶频率的平均误差为：7．07%～29．67%，而考虑翘曲变形后，计算所得平均误差仅为：0．03%～4．36%。显然，在考虑翘曲变形后，用本文方法得到的解和有限元结果吻合得很好。此外，通过计算可以发现：

（1）当材料性质和螺旋线的最大、最小半径，螺旋角，有效圈数，以及截面面积都相同的情况下，双曲形弹簧的刚度最大，其频率最高，锥形弹簧次之，桶形弹簧的频率最低。

（2）随着螺旋角、有效圈数和圆柱螺旋线半径的增大，弹簧的长度增加，系统的刚度减小，其固有频率随之减小。其中，螺旋角对频率的影响相对是最小的。

（3）对于对称层合复合材料矩形截面的双曲形弹簧来说，随着有效圈数n的增加，其2和3阶频率变得越来越接近。

［1］ 成洁．车辆悬架系统的非线性振动特性研究［D］．西安：西北工业大学，2006．

Cheng Jie．Research on vibration characteristic of nonlinear for vehicle suspension system ［D］．Xi’an：Northwestern Polytechnical University，2006．

［2］ 凌恺夫．圆锥螺旋弹簧在机车车辆上应用的研究［J］．株洲工学院学报，2001，15（3）：48—51．

Ling Kaifu．Application research of cone spiral spring on locomotive vehicle［J］．Journal of Zhuzhou Institute of Technology，2001，15（3）：48—51．

［3］ 王纪瑞，左曙光，雷镭．基于 MSC．Marc的中凸螺旋弹簧刚度特性研究［J］．佳木斯大学学报（自然科学版），2009，27（6）：807—810．

Wang Jirui，Zuo Shuguang，Lei Lei．Simulation of static and dynamic stiffness characteristics of convex coil spring based on MSC．Marc［J］．Journal of Jiamusi University（Natural Science Edition），2009，27（6）：807—810．

［4］ 李蕾．整枝机传动机构中矩形截面弹簧的研究［D］．北京：北京林业大学，2008．

Li Lei．The analyzing of the spring with rectangular section in the pruning mechine′s transmission equipment［D］．Beijing：Beijing Forestry University，2008．

［5］ 隋刚，范勇峥，仲伟虹，等．复合材料圆柱螺旋弹簧的制造与实验研究［J］．复合材料学报，2001，18（1）：46—49．

Sui Gang，Fan Yongzheng，Zhong Weihong，et al．Manufacture and experiment study of composite cylindroids spiral spring［J］．Acta Materiae Compositae Sinica，2001，18（1）：46—49．

［6］ Yildirm V．Governing equations of initially twisted elastic space rods made of laminated composite materials［J］．International Journal of Engineering Sciences，1999，37（8）：1 007—1 035．

［7］ Yildirm V．Free vibration characteristics of composite barrel and hyperboloidalcoil springs［J］．Mechanics of Composite Materials and Structures，2001，8（3）：205—217．

［8］ Yildirm V．A parametric study on the natural frequencies of unidirectional composite conical springs［J］．Communications in Numerical Methods in Engineering，2004，20（3）：207—227．

［9］ Yu A M，Hao Y．Free vibration analysis of cylindrical helical springs with noncircular cross－sections［J］．Journal of Sound and Vibration，2011，330（11）：2 628—2 639．

［10］郝颖，虞爱民．考虑翘曲效应的圆柱螺旋弹簧的振动分析［J］．力学学报，2011，43（3）：561—569．

Hao Ying，Yu Aimin．Vibration analysis of cylindrical helical springs considering warping deformation effect［J］．Chinese Journal of Theoretical and Applied Mechanics，2011，43（3）：561—569．

［11］Xu R Q，He J S，Chen W Q．Saint－Venant torsion of orthotropic bars with inhomogeneous rectangular cross section［J］．Computers ＆ Structures，2010，92（6）：1 449—1 457．

［12］刘保国．一维不定参数结构系统的摄动Riccati传递矩阵方法及其应用［D］．重庆：重庆大学，2002．

Liu Baoguo．Perturbation RICCATI transfer matrix method for one dimensional structure with parameter uncertainties and its applications［D］．Chongqing：Chongqing University，2002．

［13］王正．Riccati传递矩阵法的奇点及其消除方法［J］．振动与冲击，1987，2（22）：74—78．

Wang Zhen．The singularity and its eliminating methods of Riccati transfer matrix method［J］．Journal of Vibration and Shock，1987，2（22）：74—78．

［14］虞爱民，瞿志豪．自然弯曲与扭曲细长梁广义变分原理的研究［J］．上海冶金专科学校学报，1994，15（3）：1—8．

Yu Aimin，Qu Zhihao．The study of variational principle in naturally curved and twisted slender beams［J］．Journal of Shanghai Technical College of Metallurgy，1994，15（3）：1—8．

［15］沈观林，胡更开．复合材料力学［M］．北京：清华大学出版社，2006．

Shen Guanlin，Hu Gengkai．Mechanics of Composites［M］．Beijing：Tsinghua University Press，2006．

［16］郝颖，虞爱民．矩形截面非圆柱螺旋弹簧的模态分析［J］．振动工程学报，2012，25（3）：323—329．

HAO Ying，YU Ai－min．Modal analysis of non－cylindrical helical springs with rectangular cross－section［J］．Journal of Vibration Engineering，2012，25（3）：323—329．