极坐标系下弹性问题的重心插值配点法

李树忱，王兆清，袁超

(1. 山东大学 岩土与结构工程研究中心，山东 济南，250061；2. 山东建筑大学 工程力学研究所，山东 济南，250101 )

弹性力学是研究岩石变形、断裂破坏问题的重要基础，对于复杂的岩石弹性力学问题一般很难得到问题的解析解，数值计算方法成为一种重要的研究手段。研究弹性力学问题的基本数值方法有有限元方法和有限差分法。有限元方法是一种基于低阶多项式插值的Galerkin方法，其计算精度依赖于单元大小和积分点数量的选取；有限差分法采用差分算子近似微分算子，其计算精度依赖于差分步长的大小。近年来兴起的各种类型无网格方法，在岩石力学领域得到广泛关注[1-3]。能够采用较少的计算代价，得到问题的高精度数值解，是数值分析领域研究者努力寻求的目标。基于移动最小二乘法的无单元Galerkin法尽管有不需要划分计算网格的优点，但在形成刚度矩阵过程中，需要进行大量的计算，并且不能直接施加边界条件[3-4]。基于自然邻点插值的自然单元法，边界条件施加方便，但在形成刚度矩阵过程中，需要寻找自然邻点，计算工作量巨大[5]。Lagrange插值是函数近似的重要手段，但当插值节点数量加大时，Lagrange插值表现为数值不稳定，Runge现象说明了这一问题，因此，工程计算中较少采用 Lagrange插值作为近似未知函数的手段。将Lagrange插值公式改写为重心公式形式，得到重心Lagrange插值[6]。重心Lagrange插值具有很好的数值稳定性[7]和极高的插值近似精度[8-9]。采用重心Lagrange插值作为未知函数的近似函数的配点型方法 —— 重心插值配点法，不需要划分计算网格，也不需要数值积分，已应用于求解一维工程边值问题[10]和动力学问题[11-12]中。现有的大部分数值方法是在直角坐标系下求解弹性力学问题。对于一些圆形区域上的工程问题，例如岩石力学的巴西圆盘实验，采用极坐标系分析非常方便[13-14]。在此，本文采用重心Lagrange插值的张量积形式作为二维问题未知函数的近似函数，基于极坐标系下弹性力学位移平衡方程的强形式，提出求解极坐标系下弹性力学问题的重心插值配点法。

1 重心Lagrange插值及其微分矩阵

考虑定义在区间[a,b]上的函数u(x)，函数u(x)在节点a=x1＜x2＜…＜xn=b上的取值为ui=u(xi),i=1,2, …,n。函数u(x)的重心Lagrange插值为[8]

函数u(x)的重心Lagrange插值可表示为

则函数u(x)的m阶导数可表示为

函数u(x)在节点x1,x2, …,xn处的m阶导数可表示为

2 极坐标系下弹性问题的重心插值配点法公式

2.1 极坐标系下弹性力学的基本方程

取极坐标系(r,θ)，某点P(r,θ)处的位移分量为ur和uθ，应力分量为σr和σθ和τrθ=τθr，体力分量为fr和fθ，则极坐标系下的平衡方程可表示为

位移-应变的几何关系为：

应力-应变本构关系为：

将式(9)和(11)代入式(8)，得到位移表达的平面应力问题平衡方程：

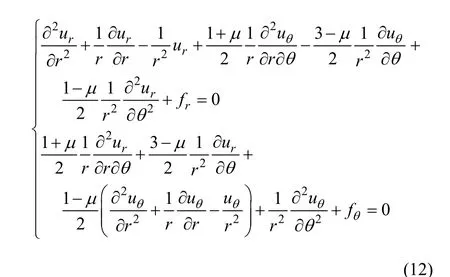
位移表达的应力分量为

对于平面应变问题，需将式(10)～(12)中的弹性常数进行下列替换：

2.2 重心插值配点法计算公式

极坐标系下平面问题的位移解法需要求解偏微分方程(式(12))的边值问题。对于几何形状和外载荷不随θ改变的轴对称结构，其应力分布与θ无关，只是坐标r的函数，方程(12)将变为常微分方程。轴对称结构常微分方程边值问题的重心插值配点法求解方法，参见文献[10]。

在求解区域Ω的r方向布置m个计算节点r1,r2, …,rm，在θ方向布置n个计算节点θ1,θ2, …,θn，构成求解区域上的m×n个张量积计算节点(ri,θj)(其中，i=1, 2, …,m;j=1, 2, …,n)。采用节点r1,r2, …,rm和θ1,θ2, …,θn上的重心 Lagrange 插值(式(1))的张量积形式插值近似径向位移ur和环向位移uθ：

其中：urij和uθij分别为径向位移ur和环向位移uθ在计算节点(ri,θk)处的值；uθij=uθ(ri,θj) ；i=1, 2, …,m;j=1, 2, …,n；Li(r),Mj(θ)分别为在节点r1,r2, …,rm和θ1,θ2, …,θn上的重心 Lagrange 插值基函数。

将式(15)代入位移表达的平衡方程(式(12))，得：

令式(16)在所有的计算节点(rk,θl)(k=1, 2, …,m;l=1, 2, …,n)成立，可得：

将径向位移ur、环向位移uθ和体力fr，fθ在计算节点(rk,θl),k=1, 2, …,m;l=1, 2, …,n处的值，排列成1个向量，表示为

其中：frij=fr(ri,θj) ；fθij=fθ(ri,θj) ；i=1, 2, …,m;j=1, 2, …,n。利用微分矩阵记号和矩阵张量积(Kronecker积)运算符号“⊗”[15]，微分方程(式(17))的矩阵表达式为：

其中：C(m)和D(m)分别为在节点r1,r2, …,rm和θ1,θ2, …,θn上的m阶重心Lagrange插值微分矩阵；Im和In分别为m阶和n阶单位矩阵；diag(1/r)，diag(1/r2)分别为函数1/r和1/r2在节点r1,r2, …,rm处函数值构成的对角矩阵。引进记号：

将式(19)简记为：

则式(21)的解耦形式为

式(22)可简记为

按照平衡方程离散的同样方式，位移表达的应力分量(式(13))的重心插值离散形式表示为

由式(24)抽取边界节点的应力分量表达式，得到应力边界条件的重心插值离散计算公式。边界条件的施加可以采用置换法或附加法[10-12]。求解代数方程方程组得到计算节点的位移值后，采用式(24)可以方便地计算出所有节点的应力。

3 数值算例

数值算例采用 MATLAB编写，以充分发挥MATLAB强大的矩阵运算能力。数值计算的绝对误差和相对误差分别定义为：

其中：Uc和Ue分别为数值计算解和解析解列向量；表示向量的 2范数。计算节点采用特殊分布的Chebyshev 节点[15]。

算例1曲梁的一般弯曲问题。考虑图1所示矩形等截面曲梁受端部载荷作用的平面应力问题。

曲梁的位移分量解析解为[16]

图1 端部受集中力作用的曲梁Fig.1 Curved beam subjected to concentrated force on end

曲梁的应力分量解析解为

曲梁的边界条件的Saint-Venant提法为：

为得到问题的高精度解答，边界条件(式(29)和(30))按照应力解析解(式(27))和位移解析解(式(26))施加。

数值计算时，曲梁的几何参数和力学参数分别取a=13，b=17，E=107，μ=0.25，P=104，单位一律采用国际单位制。不同数量Chebyshev节点重心Lagrange插值配点法计算的位移、应力误差见表1。由表1可知：采用较少数量的计算节点重心插值配点法计算的位移和应力具有很高的计算精度，并且随着计算节点数量的增加，位移和应力的计算精度随着提高；重心插值配点法计算的应力误差大于位移误差，这是由于计算应力需要数值求导造成计算精度损失。重心插值配点法计算的曲梁位移分量和应力分量分布分别见图 2～6。

算例 2含有孔洞无限大板的拉伸，应力集中因子问题。考虑如图7所示含有孔洞受单向拉伸的无限大板问题，孔洞的半径为a，板边均布拉力为P。设板的厚度为1，按照平面应力计算。

建立图7所示坐标系，极坐标系下板内应力分量的解析解为[17]：

表1 不同数量计算节点重心插值配点法计算的位移和应力误差Table 1 Computational error of displacement and stress by barycentric interpolation collocation method under different types and numbers of nodes in Example 1

图2 曲梁的径向位移分布Fig.2 Distribution of radial displacement in curved beam

图3 曲梁的环向位移分布Fig.3 Distribution of hoop displacement in curved beam

图4 曲梁的径向正应力分布Fig.4 Distribution of radial normal stress in curved beam

图5 曲梁的环向正应力分布Fig.5 Distribution of hoop normal stress in curved beam

图6 曲梁的剪应力分布Fig.6 Distribution of shear stress in curved beam

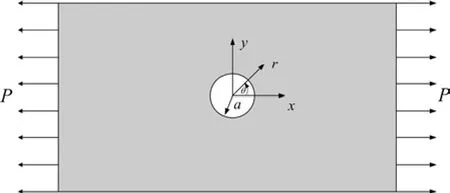
图7 含孔洞无限大板Fig.7 A infinite plate with hole under uniaxial tension

位移解析解为：

其中：G=E/ [2(1 +μ)]为剪切模量；κ= ( 3 -μ)/(1 +μ)；μ为泊松比。

图8 重心插值配点法的计算区域Fig.8 Computational domain in barycentric interpolation collocation method

r=b边界上应力边界条件按照式(33)确定：

最大环向应力 (σθ)max在孔洞边界，应力集中因子Scf=(σθ)max/P的解析值等于3，重心插值配点法计算的应力集中因子等于3.000 2。

在r方向和θ方向取不同数量计算节点计算位移和应力的相对误差，448种不同节点数量组合和相对误差常用对数的关系分别见图9～13。由图9～13可以看出：随着计算节点数量的增加，位移和应力的计算误差显著降低；在相同的径向节点数量条件下，增加环向节点数量不能明显提高计算精度；在相同的环向节点数量下，增加径向节点数量可以显著提高计算精度；在环向采用10个计算节点、径向采用33个计算节点的计算精度可达10-6量级。

上述2个算例说明：对于几何区域为圆形、圆环或扇形的弹性力学问题，采用极坐标解答可以有效地简化问题的复杂性。对于含有圆形孔洞的无限大板拉伸问题，在板中截取1个与圆孔同心的大圆，将求解区域转化为圆环区域，利用直角坐标系和极坐标系下应力的转换关系，可以方便地得到圆环求解区域的应力边界条件。

对于一般形状或不规则形状的物理区域，不能直接采用重心插值配点法计算，可以将物理区域嵌入 1个圆形或扇形的正则区域，在正则区域上采用极坐标系的重心插值配点法计算。计算得到正则区域上点的位移和应力值后，通过重心插值式(15)可以得到物理区域上任意一点的位移和应力。

表2 重心插值配点法计算的位移和应力误差Table 2 Computational error of displacement and stress in barycentric interpolation collocation method

图9 径向位移相对误差与计算节点数量的关系Fig.9 Relationship between relative error of radial displacement and number of computed nodes

图10 环向位移相对误差与计算节点数量的关系Fig.10 Relationship between relative error of hoop displacement and number of computed nodes

图11 径向应力相对误差与计算节点数量的关系Fig.11 Relationship between relative error of radial stress and number of computed nodes

图13 剪应力相对误差与计算节点数量的关系Fig.13 Relationship between relative error of shear stress and number of computed nodes

4 结论

(1) 采用重心Lagrange插值作为近似函数的重心插值配点法，在极坐标系下求解弹性力学问题，利用重心插值微分矩阵和矩阵张量积运算符号，可以将位移表达的极坐标系平衡方程的离散代数方程表示为简洁的矩阵形式。

(2) 将原来径向位移和环向位移耦合的偏微分方程组，通过矩阵操作实现解耦，这为计算程序的实施提供了极大地便利。微分矩阵的引进，提供了一种直接计算节点处应力值的简便快速方法。

(3) 重心插值配点法不需要划分计算网格，不需要数值积分，是一种真正意义上的无网格方法。

(4) 重心插值配点法具有计算格式简单、程序实施方便和计算精度高的特点。

[1] 卢波, 丁秀丽, 邬爱清. 无网格法对岩体不连续面的模拟[J].岩石力学与工程学报, 2008, 27(10): 2108-2117.

LU Bo, DING Xiuli, WU Aiqing. Modeling of rock discontinuity with meshless method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 2108-2117.

[2] 樊成, 栾茂田, 黎勇, 等. Kriging插值无网格方法及其在力学边值问题中的应用[J]. 岩石力学与工程学报, 2007, 26(1):195-200.

FAN Cheng, LUAN Maotian, LI Yong, et al. A new type meshless method based on Kriging interpolation scheme and its application to solving boundary-value problem of mechanics[J].Chinese Journal of Rock Mechanics and Engineering, 2007,26(1): 195-200.

[3] 李树忱, 李术才, 隋斌, 等. 节理岩体渗流的无网格与有限元耦合方法[J]. 岩石力学与工程学报, 2007, 26(1): 75-80.

LI Shuchen, LI Shucai, SHU Bin, et al. Coupling meshless method and finite element method for seepage of jointed rock mass[J]. Chinese Journal of Rock Mechanics and Engineering,2007, 26(1): 75-80.

[4] Belystchko T, Krongauz, Organ Y D, et al. Meshless methods:An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 185(1): 3-47.

[5] 王兆清, 冯伟. 自然单元法研究进展[J]. 力学进展, 2004,34(4): 437-445.

WANG Zhao-qing, FENG Wei. Advances in natural element method[J]. Advances in Mechanics, 2004, 34(4): 437-445.

[6] Berrut J P, Trefethen L N. Barycentric Lagrange interpolation[J].SIAM Review, 2004, 46(3): 501-517.

[7] Nicholas J H. The numerical stability of barycentric Lagrange interpolation[J]. IMA Journal of Numerical Analysis, 2004, 24(4):547-556.

[8] 王兆清, 李淑萍, 唐炳涛. 一维重心型插值: 公式、算法和应用[J]. 山东建筑大学学报, 2007, 22(5): 448-453.

WANG Zhaoqing, LI Shuping, TANG Bingtao. Formulations,algorithms and applications on barycentric interpolation in 1D[J].Journal of Shandong Jianzhu University, 2007, 22(5): 448-453.

[9] 王兆清, 李淑萍, 唐炳涛. 任意连续函数的多项式插值逼近[J]. 山东建筑大学学报, 2007, 22(2): 158-162.

WANG Zhaoqing, LI Shuping, TANG Bingtao. Polynomial interpolation approximations of arbitrary continuous functions[J].Journal of Shandong Jianzhu University, 2007, 22(2): 158-162.

[10] 王兆清, 李淑萍, 唐炳涛. 圆环变形及屈曲的重心插值配点法分析[J]. 机械强度, 2009, 31(2): 245-249.

WANG Zhaoqing, Li Shuping,Tang Bingtao. Deformation and buckling analysis of ring by barycentric interpolation collocation method[J]. Journal of Mechanical Strength, 2009, 31(2):245-249.

[11] 李淑萍, 王兆清. 非线性振动分析的重心插值配点法[J]. 噪声与振动控制, 2008, 28(4): 49-52.

LI Shuping, WANG Zhaoqing. Barycentric Interpolation Collocation Method for Solving Nonlinear Vibration Problems[J].Noise and Vibration Control, 2008, 28(4): 49-52.

[12] 王兆清, 李淑萍, 唐炳涛, 等. 脉冲激励振动问题的高精度数值分析[J]. 机械工程学报, 2009, 45(1): 288-292.

WANG Zhaoqing, LI Shuping, TANG Bingtao, et al. High precision numerical analysis of vibration problems under pulse excition[J]. Journal of Mechanical Engineering, 2009, 45(1):288-292.

[13] Hung K M, Ma C C. Theoretical analysis and digital photoelastic measurement of circular disks subjected to partially distributed compressions[J]. Experimental Mechanics, 2003, 43(2): 216-24.

[14] Ma C C, Hung K M. Exact full-field analysis of strain and displacement for circular disks subjected to partially distributed compressions[J]. International Journal of Mechanical Sciences,2008, 50(2): 275-292.

[15] Trefethen L N. Spectral methods in Matlab[M]. Philadelphia:SIAM, 2000: 211-215.

[16] Timoshenko S P, Goodier J N. Theory of elasticity[M]. New York: McGraw-Hill, 1951: 312-317.

[17] Atluri S N, Liu H T, Han Z D. Meshless local Petrov-Galerkin(MLPG) mixed collocation method for elasticity problems[J].CMES: Computer Modeling in Engineering & Sciences, 2006,14(3): 141-152.