以不变应万变:用方程解决不变量问题
2013-09-11河北刘思佳
读写算(下) 2013年11期
河北 刘思佳

解应用题时经常碰到这样一种情况:题中某些条件变幻莫测,但有一个条件始终不变,这个始终不变的量就是解题的突破口。如果再用上方程,问题就容易解决或能找到解题的思路。下文谈谈如何用方程解决不变量问题。
一、不变的类型
(一)差量不变
当差量不变时,就抓住这个不变的差量着手分析。
例1 今年妈妈50岁,小明18岁,几年前妈妈的年龄是小明年龄的5倍?
【分析】
在年龄问题中,小明长1岁,妈妈同样也长1岁,妈妈和小明的年龄差是一个不变的量,无论小明的年龄怎样变化,妈妈和小明之间的年龄差始终不变。
【解答】
解:设x年前妈妈的年龄是小明年龄的5倍。
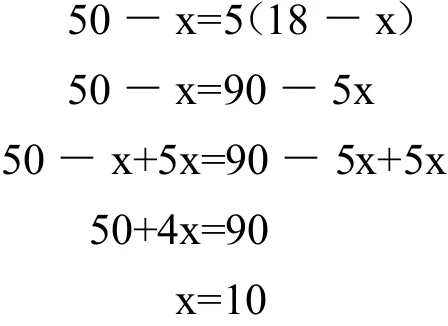
答:10年前妈妈的年龄是小明年龄的5倍。
(二)总量不变
在题中的多个量中,当只有总量不变时,要紧扣这个不变的量寻找解题思路。
例 2 幼儿园小班买来一箱草莓,每个小朋友分4个还剩48个,每个小朋友分6个又少8个,幼儿园小班有多少个小朋友?
【分析】
无论怎样分,都是分同一箱草莓,这箱草莓的个数是不变的。即:第二种分法的草莓个数=第一种分法的草莓个数。
【解答】
解:设幼儿园小班有x个小朋友。

答:幼儿园小班有28个小朋友。
二、不变量的训练
1.今年聪聪12岁,爸爸30岁,几年前爸爸的年龄是聪聪的3倍?
2.五(1)班要进行植树活动,如果每人植8棵,还剩24棵;如果每人植10棵,还差14棵。问五(1)班共有多少名学生?

