基于包容性检验和证据理论的短期负荷预测

石晓艳，刘淮霞，于水娟

（安徽理工大学 电气与信息工程学院自动化系，安徽 淮南232001）

0 引 言

负荷预测是电力规划的基础，尤其是短期负荷预测结果对保证电网安全运行，提高供电质量起着十分重要，因此，短期负荷预测成为电力研究领域的一个重要课题［1］。

传统负荷预测方法主要有线性回归 （LR）、指数平滑、差分自回归滑动平均 （ARIMA）、灰色模型GM （1，1）、趋势外推法 （TE）等［2－4］，由于短期负荷受到天气、季节、节假日等因素影响，具有时变性、不确定性和非线性等变化特点，传统预测方法的预测精度与实际要求有一定的差距。随着非线性理论不断发展，出现基于人工神经网络（ANN）、支持向量机 （SVM）等的短期负荷预测算法［5，6］，相对于传统预测模型，短期负荷预测精度得到了相应提高，但ANN基于经验风险最小化原则，易出现 “过拟合”现象，泛化预测能力差等缺陷［7］；SVM基于结构风险最小化原则，泛化能力好，但是预测效果对核函数非常敏感。基于组合理论，当前许多学者提出短期负荷的组合预测方法，由于不同模型可以从不同的角度预测负荷变化信息，相互补充，克服各自的不足，大量研究表明，组合模型的负荷预测精度和稳定性优于单项模型［8，9］。但是，在实际应用中，不可能将全部单一模型进行组合，同时，相关研究表明，随便增加单一预测模型个数并不一定提高组合模型的预测效果，而且单一模型间可能存在一定的相关性，使组合预测的输入信息重叠，导致预测准确率降低，因此，在进行组合建模预测前，选择最适合单一模型及合理确定权重。最近，有学者提出基于包容性检验的单一模型选择策略［10，11］，研究结果表明，包容性检验筛选出了适用较优单一预测模型，有利于提高组合模型的预测性能。

证据理论 （dempster－shafer theory，DS）是一种非精确的推理算法，可以有效综合不同数据源的知识，有较强的决策处理能力，可以用于确定模型的权值［12］。为了提高短期负荷预测精度，提出一种基于包容性检验和证据理论相融合的短期负荷组合预测模型。首先包容性检验方法选择最合适的单一短期负荷预测模型，然后采用证据理论确定单一模型权重，并根据权重得到短期负荷的组合预测结果，最后通过仿真实验对组合模型的性能进行测试。

1 包容性检验的单一模型选择

1.1 包容性检测原理

设M1、M2分别表示两个不同的预测模型，t时刻的实际值为yt，两模型在t时刻的预测结果分别为f1，t和f2，t，考虑如下形式的回归方程

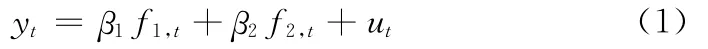
式中：ut——随机扰动；β1、β2——回归系数，且β1＋β2＝1。

式 （1）两边同时减去f1，t，则有

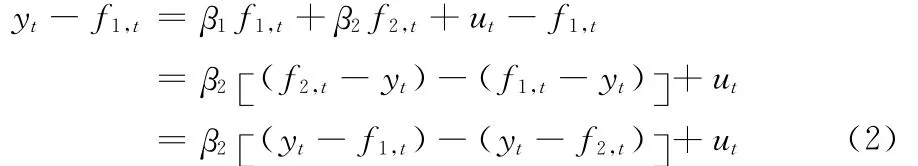
令ei，t＝yt－fi，t（i＝1，2），则式 （2）就可以转化为

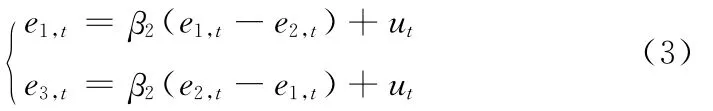
在α显著性水平下，通过检验计算回归系数β1和β2值。具体为：

（1）设H0：β＝0，H1：β≠0，其中β取值β1或β2。

（2）计算统计量。当成立时，可得

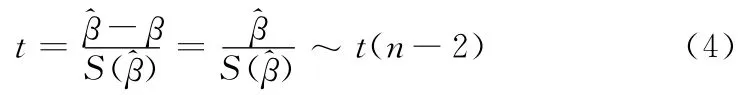
（3）在给定显著性水平α下，确定临界值tα／2（n－2）。

（5）若β1＝0且β2＝0，则表示模型M1包容模型M2；若β1≠0且β2＝0，则表示M2包容M1；其它情况表示M1与M2不包容，每个模型都包含了关于yt的有用信息。

以上是两模型组合的包容性检验原理，但是在实际应用中，一般是两个以上的模型进行组合。多模型的包容性检测步骤如下：

设f1，t，f2，t，…，fk，t分别表示t时刻分别来自k个模型的预测结果，t时 刻 的 实 际值 为yt；fc，t为 是f1，t，f2，t，…，fk，t预 测 模 型 组 合 结 果；fc（－i），t表 示 不 包 含fi，t预 测结果。

令ec，t＝yt－fc，t，ec（－i），t＝yt－fc（－i），t，在包容性检验中增加截距项，然后根据式 （4）得到多模型组合预测的包容性检验为

检验假设：H0：αi＝0，i＝1，2，…，k，在αi显著性水平下，通过t统计量检验选择模型。如果t检验显著不为0，则表示ri，t包含原有模型所不具备的信息，组合ri，t，可以提高预测效果，ri，t不能被原有模型包容，否则，表示组合ri，t对预测结果没有什么影响，删除ri，t。

1.2 单一模型选择步骤

（1）计算每个单一模型的预测结果，并将预测结果作为模型优劣的评价准则，并根据评价结果对模型进行降序排序。

（2）选择性能最好的预测模型，并根据包容性检验原则，对预测性能最好的模型依次进行检验，看其是否包容其它预测模型，若包容了其它预测模型，则将该模型从列表中删除，反之，就以一定的组合方式将它们进行预测组合，直到组合模型以外所有其它模型已被删除，那么包容性检验就完成。

（3）将当前组合模型作为最好模型，继续与其它还没有包容性检验的模型进行检验，不断重复步骤 （2）。

（4）将最后所选择单一模型作为最合适的预测模型。

2 证据理论确定的模型权值

2.1 证据理论

证据理论又称DS证据理论，能够有效表示不确定性，并对多个包含不确定性的证据源进行合成。对任意命题A，均应属于幂集2Θ，在2Θ上，若函数m：2Θ→ ［0，1］，且满足

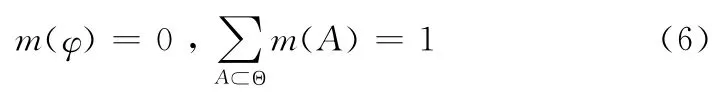
m被称为辨识框架Θ上的基本可信任分配函数。如果A为Θ的子集，且m（A）＞0，则称A为证据的焦元，所有焦元的集合称为核，证据由证据体（m，m（A））组成。

设Bel1和Bel2是同一识别框架Θ上的两个信任函数，m1和m2分别是其对应的基本可信任分配函数，焦元分别为A1，A2，…，Am与B1，B2，…，Bn，融合规则如下

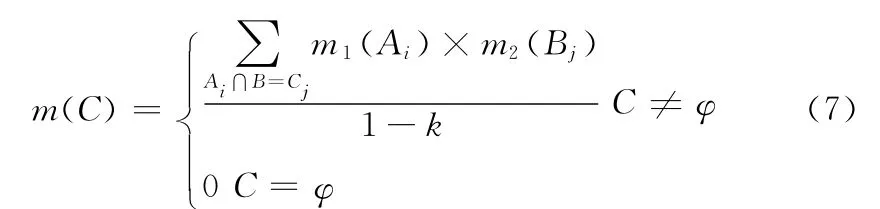
式中：k——两个证据间的冲突信息。

2.2 模型权值确定原则

根据上述包容性检验方法得到了m个短期负荷预测模型。设Mi在t时刻的负荷预测值为fi，t，t时刻的负荷实际值为yt，i＝1，2，…，m，那么Mi在t时刻的相对预测误差为。因为ei，t反映预测模型的预测值和真实值之间的误差程度，ei，t越小，表示该模型的预测值的精度更高，因此根据预测模型的相对误差，将模型分为分优、中、差3个等级，分别记为F、M、S，那么负荷预测模型识别框架的最小基本元素取为 ｛F，M，S｝。如果ei，t越小，应给该预测模型的元素F赋予较高基本信度值；反之，相赋予预测模型的元素S赋予较高基本信度值。在实际的负荷预测中，相对误差一般在10%以内，遵循以上的原则，基本信度分配见表1。然后根据式 （7）的融合规则得出相应的权值系数。

表1 基本信度分配情况

3 仿真实验

3.1 数据来源

为了验证本文短期负荷组合预测模型的性能，采用中国某地区2012年5月1日至2012年5月30日每小时负荷数据进行仿真实验，共有720个数据，收集负荷数据样本如图1所示。其中，前620个数据作为训练集，后100个数据作为验证集，用于检验组合预测模型的性能。

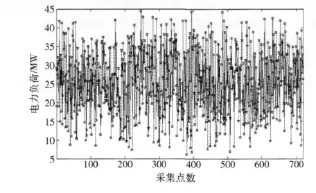
图1 收集短期负荷数据

3.2 数据的预处理

以避免样本数据值过大或过小影响模型的训练，在建模之前，对负荷数据进行预处理，具体如下

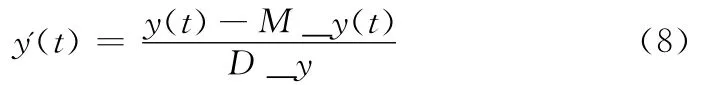
式中：M＿y（t），D＿y——负荷数据的均值和方差。

3.3 单一模型预测结果

为了使单一模型具有代表性，选择LR、TE、ARI－MA、GM （1，1）、BP神经网络 （BPNN）、SVM 作为初始单一模型。首先采用单一模型对负荷的训练集进行学习，建立相应的负荷预测模型，然后采用建立的负荷预测模型对验证集进行测试，最后计算验证集的预测结果均方根误差 （root mean squared error，RMSE），见表2。从表2可知，非线性预测模型的预测性能要优于传统的线性模型，但是单一模型的预测误差均较大，难以满足短期负荷预测的实际要求。

表2 单一模型预测结果的RMSE

3.4 选择最适合的单一预测模型

（1）根据表2单一模型预测结果的RMSE对模型进行排序，得到的排序为：SVM、BPNN、ARIMA、GM （1，1）、TE、LR，将这些模型按顺序输入到待评表。选择SVM为基本模型，将其从待评表移至备选表中。

（2）在a＝0.05的显著性水平下，将SVM对BPNN进行包容性检验，t统计量为－2.188，不显著，这表示SVM包容BPNN，因此将BPNN从待评表中删除。

（3）在a＝0.05的显著性水平下，将SVM对ARIMA进行包容性检验，t统计量为3.920，显著不为0，SVM不能包容ARIMA，因此采用证据理论将SVM和ARIMA进行组合，组合模型记为SVM－ARIMA。

（4）在a＝0.05的显著性水平下，将SVM－ARIM对GM （1，1）进行包容性检验，t统计量为2.775，显著不为0，SVM－ARIMA不能包容GM （1，1），因此采用证据理论将SVM－ARIMA和GM （1，1）进行组合，组合模型记为SVM－ARIMA－GM （1，1）。

（5）采用上述相同方法，对所有单一模型进行包容性检验，直到待评表为空，停止包容性检验，最后选择的最合适单一模型为：SVM、ARIMA、GM （1，1）。

3.5 仿真结果与分析

3.5.1 ET－DS与其它组合模型的预测结果对比

采用包容性检验选择的SVM、ARIMA、GM （1，1）对短期负荷进行预测，然后采用证据理论根据预测结果的相对误差得到SVM、ARIMA、GM （1，1）的加权系数为：（0.4008，0.3355，0.2637），最后得到 ET－DS的负荷预测模型的预测结果如图2所示。同时为了让ET－DS的预测结果更具说服力，采用传统线性加权平均组合模型作为对比模型，其预测结果如图3所示。

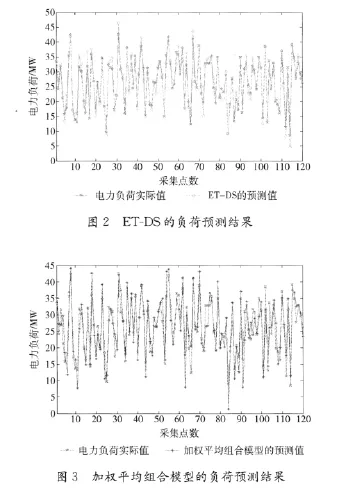
从图2和3可知，组合模型的预测值与实际短期负荷值相当接近，比较吻合，而且预测结果十分稳定。而线性加权平均组合模型的预测结果不稳定，有些预测值与实际短期负荷值偏差较大，这主要是由于线性加权不能准确体现各模型对组合模型预测结果的贡献，而本文通过引入证据理论确定单一模型的权值，可以明显区分每个模型对最终预测结果的贡献，大大提高了负荷预测的精度，仿真对比结果表明，采用包容性检验和证据理论相融合的短期负荷组合预测模型是一种预测精度高、结果可靠的短期负荷预测模型。

3.5.2 组合模型与单一模型综合性能对比

采用平均绝对误差 （MAE）、均方根误差 （RMSE）、平均绝对百分比误差 （MAPE）、均方百分比误差 （MSPE）作为短期负荷预测模型性能的评判准则。它们具体定义如下

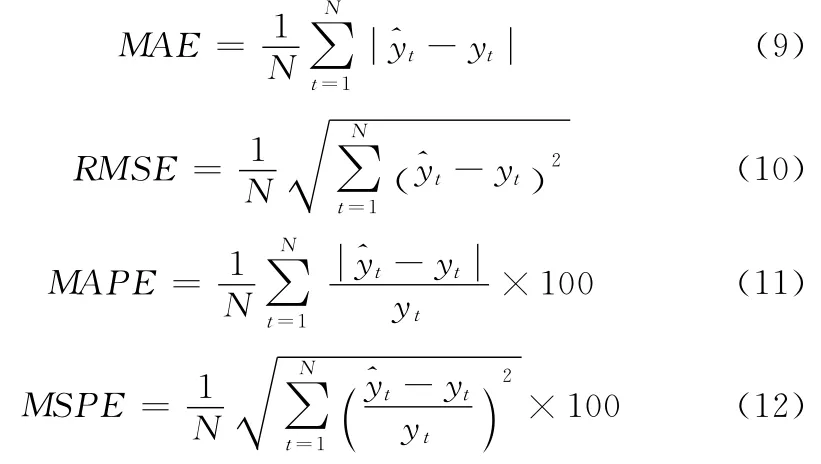
式中：yt——t时刻实际短期负荷，＾yt——模型预测的短期负荷，N——验证样本数。

ET－DS模型和单一预测模型的综合性能见表3。从表3可知，相对于单一模型，ET－DS模型提高了短期负荷预测精度，各项预测误差指标均小于单项预测模型，主要是组合模型可以从多角度描述短期负荷变化趋势，降低信息的不完备性，使预测值与实际值更加吻合。

综合上述可知，ET－DS模型首先通过包容性检验选择最适合的负荷预测模型，然后通过证据理论科学确定单一模型的权值，更加有效地反映了复杂多变的短期负荷变化趋势，有效提高了短期负荷预测精度。

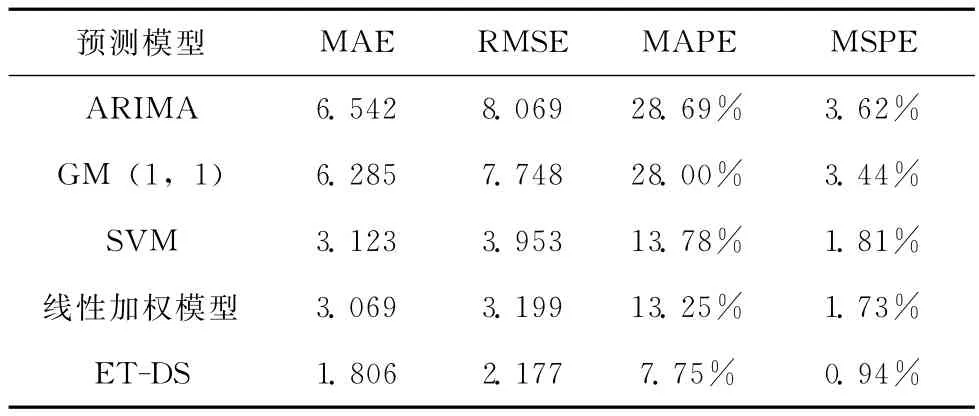
表3 各模型的综合预测性能对比

4 结束语

短期负荷预测是电力市场的重要组成部分，其精度直接影响到电力系统的经济效益，由于短期负荷受天气情况、节假日、人口基数、经济指标、消费指数等因子影响，呈现时变性、不确性、非线性变化趋势，采用单一模型无法准确反映其复杂变化特点，为此提出一种包容性检测和证据理论结合的短期负荷组合预测模型。分别采用包容性检验方法和证据理论选择最合适预测模型和确定模型权重，仿真结果表明，ET－DS模型提高了短期负荷的预测精度，使预测误差更小，并为其它复杂系统的预测提供一种研究思路。

［1］LIAO Nihuan，HU Zhihong，MA Yingying，et a1.Review of the short－term load forecasting methods of electric power system［J］.Power System Protection and Control，2011，39 （1）：147－152（in Chinese）.［廖旎焕，胡智宏，马莹莹，等.电力系统短期负荷预测方法综述 ［J］.电力系统保护与控制，2011，39 （1）：147－152.］

［2］FANG Gefei，HU Changhong，ZHENG Yihui，et a1.Study on the method of short－term load forecasting considering summer weather factors ［J］.Power System Protection and Control，2010，38 （22）：100－104（in Chinese）.［方鸽飞，胡长洪，郑奕辉，等.考虑夏季气象因素的短期负荷预测研究方法 ［J］.电力系统保护与控制，2010，38 （22）：100－104.］

［3］LI Po，LI Min，LIU Dichen.Power load forecasting based on improved regression［J］.Power System Technology，2006，30（1）：99－104.

［4］ZHANG Junfang，WUYiang，WU Junji.Application of grey system theory in load forecasting ［J］.Electric Power Automation Equipment，2004，24 （5）：24－27（in Chinese）.［张俊芳，吴伊昂，吴军基.基于灰色系统理论负荷预测的应用研究［J］.电力自动化设备，2004，24 （5）：24－27.］

［5］PENG Xiangang，HU Songfeng，LV Dayong.Review on grid short－term load forecasting methods based on RBF neural network ［J］.Power System Protection and Control，2011，39（17）：144－148（in Chinese）.［彭显刚，胡松峰，吕大勇.基于RBF神经网络的短期负荷预测方法综述 ［J］.电力系统保护与控制，2011，39 （17）：144－148.］

［6］WANG Deyi，YANG Zhuo，YANG Guoqing.Short term load forecasting based on chaotic characteristic of loads and least squares support vector machines ［J］.Power System Technology，2008，32 （7）：66－71（in Chinese）.［王德意，杨卓，杨国清.基于负荷混沌特性和最小二乘支持向量机的短期负荷预测 ［J］.电网技术，2008，32 （7）：66－71.］

［7］WU Jinglong，YANG Shuxia，LIU Chengshui.Parameter selection for support vector machines based on genetic algorithms to short－term power load forecasting ［J］.Journal of Central South University：Science and Technology，2009，40 （1）：l80－184（in Chinese）.［吴景龙，杨淑霞，刘承水.基于遗传算法优化参数的支持向量机短期负荷预测方法 ［J］.中南大学学报 （自然科学版），2009，40 （1）：180－184.］

［8］LI Guangzhen，LIU Wenying.Bus load short－term forecast based on LSSVM and Markov chain ［J］.Power System Pro－tection and Control，2010，38 （11）：55－59（in Chinese）.［李光珍，刘文颖.基于LSSVM和马尔可夫链的母线负荷短期预测 ［J］.电力系统保护与控制，2010，38 （11）：55－59.］

［9］ZHU Yanping，FANG Gefei.Short－term load forecasting based on dynamic adaptive artificial neural network and human body amenity indicator ［J］.Power System Protection and Control，2012，40 （11）：56－61（in Chinese）.［祝燕萍，方鸽飞.基于动态自适应神经网络和人体舒适度的短期负荷预测 ［J］.电力系统保护与控制，2012，40 （1）：56－61.］

［10］XIE Li，WEI Ruxiang，ZI Shuyu，et al.Combined forecasting of ship equipment maintenance cost based on encompassing tests［J］.Systems Engineering and Electronics，2010，32（12）：2599－2602 （in Chinese）.［谢 力，魏 汝 祥，訾 书 宇，等.基于包容性检验的舰船装备维修费组合预测 ［J］.系统工程与电子技术，2010，32 （12）：2599－2602.］

［11］LI Hongan，KANG Baosheng，ZHANG Jing，et al.Combined forecasting of cloud computing resources on improved encompassing tests ［J］.Application Research of Computers，2013，30 （1）：252－255（in Chinese）. ［李洪安，康宝生，张婧，等.基于改进的包容性检验的云计算资源组合预测 ［J］.计算机应用研究，2013，30 （1）：252－255.］

［12］Nhan N，Insoo K.An enhanced cooperative spectrum sensing scheme based on evidence theory and reliability source evaluation in cognitive radio context ［J］.IEEE Communications Letters，2009，13 （7）：492－494.