基于不同载重与车速的简支梁桥动力响应*

谭红霞，李建男，黎 略，王晶晶

(湘潭大学土木工程与力学学院，湖南 湘潭 411105)

基于不同载重与车速的简支梁桥动力响应*

谭红霞，李建男，黎 略，王晶晶

(湘潭大学土木工程与力学学院，湖南 湘潭 411105)

采用振型分解法求解车桥耦合振动方程，分析简支梁桥在不同载重和车速作用下的动力响应.车辆采用1/2车模型，简支梁桥采用欧拉梁，建立车桥耦合振动方程，运用Ansys软件，得出简支梁桥跨中挠度变化曲线.结果表明，车辆载重的增加导致桥梁跨中挠度增加，车辆标准载重及车辆超载100%时跨中挠度分别为0.028，0.049 m.随着车辆速度增加，简支梁桥跨中挠度在车速60 km/h时达到峰值，此时桥梁与车辆产生共振.

动力响应;车桥耦合方程;半车模型;载重与速度

公路桥梁在交通运输中是不可缺少的组成部分，其运营状况关系到道路交通运输的畅通.车辆通过桥梁引起桥梁振动，一方面会对桥梁结构产生冲击作用，致使结构出现过大变形或者开裂，另一方面会使其结构出现内部损伤，加速结构原有损伤，甚至会导致桥梁垮塌.［1-3］桥梁结构的过大振动会影响车辆通行的舒适度、平稳性和安全性［4-5］，因此研究车辆桥梁之间的耦合振动，考虑载重与车速对桥梁跨中挠度的影响，以便于对桥梁结构的振动性能和安全运营进行评估［6-7］.

笔者利用简化的1/2车辆模型及不考虑阻尼的欧拉梁建立车桥耦合振动方程，运用振型分解法求解桥梁在不同载重与速度车辆作用下的动力响应.运用Ansys软件模拟车桥耦合动力响应，得到简支梁桥在不同载荷即不同车速作用下的跨中挠度动力响应.

1 车辆模型的选取

汽车结构比较复杂，是一个空间多自由度系统［8］.因此，为了更好地反应简支梁桥本身的动力特性，文中忽略车辆局部零件的振动，只考虑车辆和桥梁的竖向振动.假设车体为刚体，用2根弹簧联结并支撑于轮胎上，忽略车辆的左右摆动，只考虑桥梁的竖向振动和俯仰振动.

模型简化过程中，为保证车辆空间整体性，因此必须保证车辆前后轴的质量分布和位置.设前后轴质量分配为2

为转动惯量;汽车前后轴距lc=l1+l2，l1，l2为车炳重心C至前后车轴的距离.

2 建立车桥耦合方程

车辆作用下，车桥耦合的振动模型如图1所示.

选用欧拉-伯努利桥梁有限元模型，即含有2个端节点的1维单元，单元的变形有水平向的ν和转角θ，桥梁模型为2维模型，不考虑偏载影响，则车辆荷载可表示为

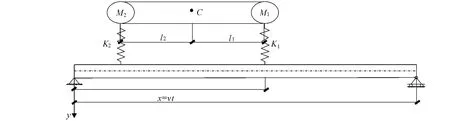
图1 车桥耦合振动模型

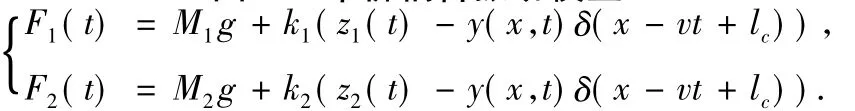
其中:z1，z2分别为汽车前后轴弹簧上质量;M1，M2为由静平衡位置算起的绝对位移.

令

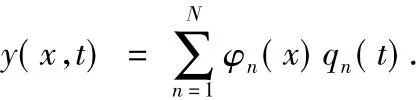
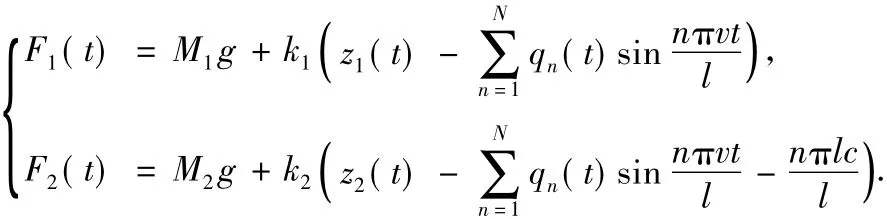
由于车辆的悬挂弹簧刚度远小于梁的抗弯刚度，车辆弹簧的产生的绝对位移比梁的挠度要大得多，忽略汽车悬挂阻尼，因此

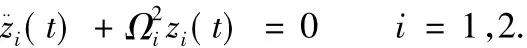
当汽车以匀速v上桥的瞬时，可测出车体的竖向位移z0i、速度z·0i、加速度z¨0i中的任2个.于是，车辆的初始条件方程的解可表示为

其中Ai为由初始条件确定的振幅，αi为由初始条件确定的相位.车辆对简支梁的作用力为

由对简支梁的各阶振型可得广义扰动力.

无阻尼的Euler-Bernoulli梁的各阶振型和强迫振动方程为

其中n=1，2，3，…，N.(1)式的N个方程对应着N振型，应用振型分解法可求解上述常系数方程组.

利用三角函数变换关系可得

引入Ωv=nπvt/l，(2)式的稳态解可写为

将该稳态解输入Ansys中，求解耦合方程得到简支梁桥跨中响应.

3 不同载重与速度作用下简支梁动力响应

文中运用Ansys软件，选用Beam3桥梁模型，将桥梁模型划分为50个有限单元，分别求解车辆以40 km/h的速度上桥在18，25，36 t这3种荷载作用下简支梁桥的跨中挠度动力响应，并求解了在18，25 t载重情况下车速分别以40，60，80，1 20 km/h上桥的跨中动力响应.简支梁桥参数及车辆参数如表1所示［9］.

表1 简支梁桥与车辆相关参数

工况1:车辆行驶速度为40 km/h，车辆载重分别为18，25，36 t时的桥梁跨中动力响应如图2所示.由图2可知，简支梁桥的跨中挠度最大值随着载重的增加而增大.当车辆荷载由18 t依次增大到25，36 t，简支梁桥跨中挠度分别为0.028，0.033，0.049 m.动力响应结果与文献［6］相似.

工况2:车辆载重为18 t，分别以40，60，80，120 km/h的车速上桥时的桥梁跨中动力响应如图3所示.由图3可知，车辆速度分别为40，60，80，120 km/h上桥时跨中挠度分别为0.028，0.032，0.030，0.023 m.桥梁跨中挠度在车速6 0 km/h时达到最大，但在车速80，120 km/h时挠度减小，该结果与文献［7］结果相符.

工况3:车辆载重为25 t，分别以40，60，80，120 km/h的车速上桥时的桥梁跨中动力响应如图4所示.由图4可知，车辆速度分别为40，60，80，120 km/h上桥时跨中挠度分别为0.033，0.041，0.026，0.032 m，与工况2结果类似，桥梁跨中挠度在车速60km/h时达到最大，但在车速80，120km/h挠度减小.

图2 不同载重作用下桥梁跨中动力响应

图3 载重18 t下不同车速的桥梁跨中动力响应曲线

图4 载重25 t下不同车速的桥梁跨中动力响应曲线

4 结语

文中以车桥耦合振动模型为研究对象，分析了简支梁桥在不同车载和车速作用下的动力响应.通过仿真计算得到以下结论:(1)简支梁桥的跨中挠度随车辆载重增加而增大，车辆载重增大1倍则挠度增加近1倍时;(2)跨中挠度的峰值并不一定出现在车辆在桥梁跨中的位置，而是出现在跨中左右;(3)车辆速度对简支梁桥跨中挠度有影响，但并不成正比增长，车速在60 km/h时出现最大值，这表明桥梁在该速度下产生共振;(4)相对于车辆的速度来说，车辆载重对桥梁的动力响应影响更大.

［1］ 赵 青.汽车超载行驶对简支梁桥振动响应的影响分析［J］.河北工业大学学报，2009，38(5):114-118.

［2］ 王元丰，许士杰.桥梁在车辆作用下空间动力响应的研究［J］.中国公路学报，2000(4):39-43.

［3］ 向天宇，赵人达，刘海波.基于静力测试数据的预应力混凝土连续梁结构损伤识别［J］.土木工程学报，2003(11):7 9-82.

［4］ 谢秉敏，向中富，王小松，等.基于ANSYS的车桥耦合动力分析［J］.重庆交通大学学报:自然科学版，2012，31(5):935 -938.

［5］ 董传磊.简支梁桥在车辆荷载作用下的振动响应影响因素分析［J］.中国西部科技，2010，9(9):39-41;43.

［6］ 蔡 晶，吴智深，李兆霞.静力荷载作用下结构参数识别及状态评估的统计分析［J］.工程力学，2004(6):76-83.

［7］ 余 华，吴定俊，项海帆.移动荷载过桥的精细计算［J］.振动与冲击，2009(5):17-21;201.

［8］ 宋一凡.公路桥梁动力学［M］.北京:人民交通出版社，2000.

［9］ GNOZALEZ A，OBRIEN E J.Identification of Damping in a Bridge Using a Moving Instrumented Vehicle［J］.Journal of Sound and Vibration，2012，331:4 115-4 131.

［10］ 施 颖，宋一凡，孙 慧，等.基于ANSYS的公路复杂桥梁车桥耦合动力分析方法［J］.天津大学学报，2010，43(6): 537-543.

(责任编辑 陈炳权)

Simply-Supported Beam Bridge’s Dynamic Response to the Different Vehicle Speed and Loaded

TAN Hong-xia，LI Jian-nan，LI Lüe，WANG Jing-jing
(College of Civil Engineering and Mechanics，Xiangtan University，Xiangtan 411105，Hunan China)

Using modal decomposition method for solving vehicle-bridge coupling equation to analyze the dynamic response of the simply-supported beam bridge to different vehicle load and speed.The half car model was used as vehicle，and Euler-Bernoulli beam was used as the simply-supported beam bridge.U sing the ANSYS software，the simply-supported beam bridge span deflection curve was obtained.The results show that vehicle load increase made the bridge span deflection increase;the beam’s span deflections were 0.028 m and 0.049 m respectively in the standard vehicle load and 100%vehicle overload.As the vehicle speed increased，the simply-supported beam bridge span deflection reached at its peak value at the vehicle speed of 60 km/h and vehicle-bridge resonance was resulted in.

dynamic response;vehicle-bridge coupling equation;half car model;load and speed

U441

A

10.3969/j.issn.1007-2985.2013.02.019

1007-2985(2013)02-0087-04

2013-01-20

谭红霞(1969-)，女，湖南湘潭人，湘潭大学土木工程与力学学院副教授，博士，主要从事大跨度桥梁理论研究

李建男(1985-)，女，河北邯郸人，湘潭大学土木工程与力学学院硕士生;主要从事桥梁监测及损伤识别研究.