“简化”“定向”助你快速填出运算符号

◎湖南 胡宏伟

这种题可以分以下几步去解决：

首先，寻找特点。这些算式要填三个运算符号，显然是三步计算的混合运算，而且等号左边的数相同。

其次，简化算式。可以把这些算式三步计算简化为一步计算来思考。例如，像下面一样把画线的部分看成一个整体，就把三步计算简化成了一步计算。

然后，定向试填。先确定一个相等的一步计算式，再分别试填运算符号满足一步计算式的需要，从而使整个混合运算式两边相等。例如：

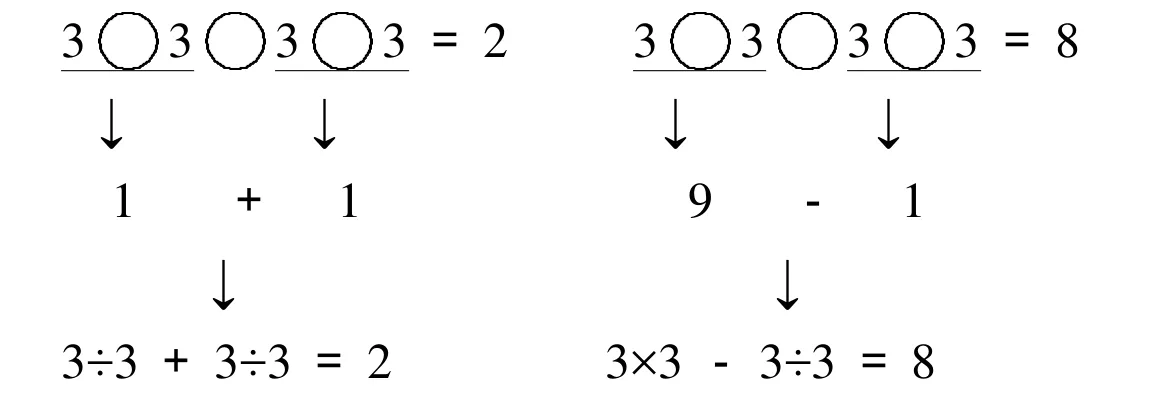
最后，多向思考。换一个相等的一步计算式，很多时候还可以获得其他填法。例如：填3333＝1的计算符号，可以这样想：得数是1的加减乘除的计算有：同数(0除外)相除等于1；1×1＝1；0+1＝1或1+0＝1；相邻的自然数相差1。可以获得下面四类填法。

一、简化为同数(0除外)相除的形式来填

（1）（3+3）÷（3+3）＝ 1

（2）（3×3）÷（3×3）＝ 1

（3）（3÷3）÷（3÷3）＝ 1

（4）3×3÷3÷3 ＝ 1

（5）3÷3×3÷3 ＝ 1

二、简化为1×1＝1的形式来填

（3÷3）×（3÷3）＝ 1

三、简化为1+0=1或0+1=1的形式来填

（1）3÷3+(3 － 3)＝ 1

（2）(3－3)+3÷3＝1

（3）3－3+3÷3＝1

四、简化为相邻的自然数相减等于1的形式来填

（1）3－（3－ 3÷3）=1

（2）3÷3－（3－ 3）=1

（3）3÷3+3－3＝1

（4）3+3÷3－3＝1

多步混合运算要填运算符号，最重要的是“简化”“定向”两个步骤，它们能帮助同学们快速填出运算符号。

聪明的小读者，你能将题目中的另几题做出来吗？试试看。