基于小波变换与统计分析的转子碰摩声发射特性研究

于 洋，杨 平，杨理践

(沈阳工业大学 信息科学与工程学院，沈阳 110870)

转子碰摩是旋转机械常见故障之一，86%弯轴事故由转子碰摩引起［1］，因此转子碰摩检测一直是机械故障诊断领域研究热点［2］。徐尉南等［3］采取数值仿真模拟方法研究转子碰摩，得出转子碰摩后会出现转子与静子持续全周碰摩现象。孟传民等［4］认为碰摩初期振动信号常被转子系统本身振动信息湮没，造成碰摩信息难以检测。Mba等［5-7］认为与振动检测相比，声发射技术对旋转机械早期损伤更敏感。故将声发射技术用于转子碰摩检测，颇受关注。

声发射指材料局部、表面源迅速释放能量，并在结构中以波形式传播的现象［8-9］。Hall等［10］用 KS(柯尔莫哥罗夫-斯米尔诺夫)统计法对转子碰摩声发射信号进行区分，认为该方法在区分转子局部碰摩损伤中具有很大潜力。Leahy等［11］对涡轮机转子碰摩进行声发射检测，认为声发射检测转子碰摩具有可行性。邓艾东等［12］提出应用声发射信号频谱判断碰摩状态及发展趋势。成新民等［13］提出用代数神经网络，将关联维数等参数作为输入，能有效降低学习时间。Saad等［14］认为声发射数据处理、合理解释及分类是限制声发射技术在机械故障检测领域进一步应用难题。

本文应用时频分析方法小波变换研究转子转速、传感器监测位置与碰摩声发射信号时频细节特征关系，探讨解决声发射数据解释及分类问题。

1 小波变换与声发射信号

1.1 小波变换

小波变换为时间窗与频率窗均可改变的时频局部化分析方法，较适合探测正常信号中夹带的瞬态反常现象并展示其成分。对任意平方可积函数f(t)∈L2(R)的连续小波变换定义为:

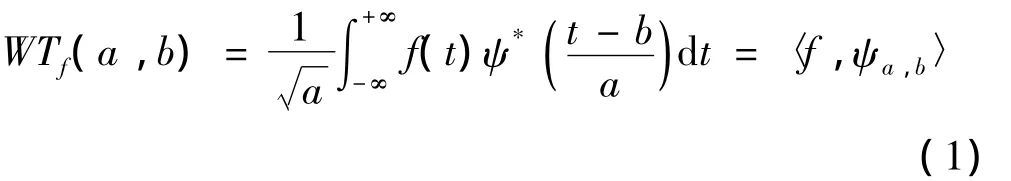
式中:a为尺度因子，b为平移因子，ψ为母小波。

在连续小波变换中，令尺度因子参数a=2-j，平移因子b=k2-j，j，k∈Z，则离散小波变换定义为:

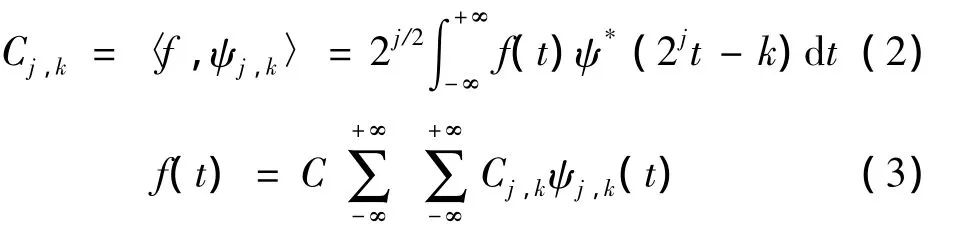
式中:C为与信号无关的常数。

1.2 小波基函数性质

小波基函数以小波基处理信号为依据，小波基函数性质为:

(1)紧支性

若函数φ(x)在［a，b］之外取值均为零，则称φ(x)是紧支的，［a，b］即为其支集。紧支是小波特有性质之一，在信号突变检测中，支集区间越小，越有利于确定信号突变点，但同时会失去好的正则性，不存在时域频域同时紧支的小波基，通常紧支小波指时域紧支小波。

(2)正则性

设函数φ(x)的N阶导数存在，对任意x，β∈R，若有:

式中:0＜α＜1;c为与x，β无关的常数，称φ(x)具有N+α阶正则性。正则性越高，函数越光滑，频域能量越集中。

1.3 dB小波及声发射信号

(1)dB小波

dB函数由Daubechies［15］构造一大类具有高阶消失矩的紧支撑正交小波函数，表达式为:

(2)声发射信号

虽目前尚无确切公式可描述机械损伤与声发射信号关系，但不同传感器接收的声发射信号可表示为［16］:

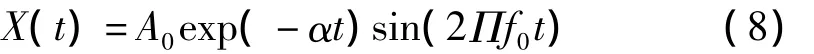
式中:A0为信号初始幅值，α为材料阻尼，f0为传感器谐振频率。

1.4 小波基函数选择

小波提取信号特征本质为用已知小波函数与被分析信号进行积分运算，通过积分结果判断采集的信号特征。故小波基函数的选择主要据被处理信号特点及提取信号特征进行选择。

理论上传感器接收的声发射信号见图1。由图1及式(8)可看出，声发射信号具有冲击性质且呈指数振荡快速衰减。故要求小波函数既有较短支集，亦有较高消失矩及一定正则性。图2为dB8小波波形，通过对常用小波基函数图形对比分析，dB8小波与经验声发射信号波形较相似故用dB8小波处理声发射信号较合适。

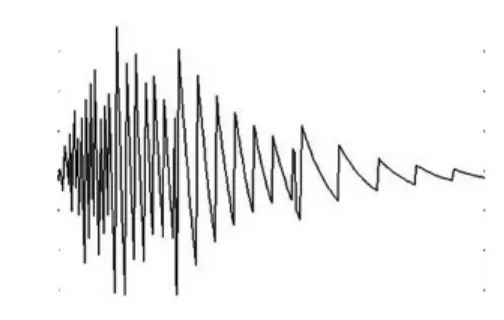
图1 理想声发射波形Fig.1 Theoretical waveform

图2 db8小波波形Fig.2 dB8 wavelet waveform

对分级层次，主要视所处理信号最低频率分辨率，表达式为:

其中:fs为采样率，J为分解层次，实验中fs为2 000 kHz，传感器频率范围为100～1 000 kHz，计算结果J至少大于等于4才能满足结果。

2 碰摩实验研究

2.1 实验装置

碰摩实验测试系统由挠性转子实验台、PCI-2声发射测试系统组成(图3)。挠性转子实验台由底座、变频电机、联轴器、支架、滑动轴承、轴及圆盘组成，图中1、2代表传感器位置，圆盘直径78 mm，厚20 mm;轴直径10 mm，长156 mm;滑动轴承外径24 mm，宽25 mm;轴承套直径34 mm，宽30 mm。

图3 实验台Fig.3 Experimental rig

实验中采用 Wsa宽频传感器，频带范围100～1 000 kHz;前置放大器放大倍数40 dB，带宽100～1 000 kHz;采集卡PCI-2卡，门槛值40 dB，采样频率2 MHz，峰值、撞击锁定时间为200，800，1 000 μs。实验过程:在图3中圆盘上，碰摩位置距传感器1支架直线距离96 mm，距传感器2支架直线距离60 mm。传感器中心与轴心距离54 mm，传感器直径20 mm。用支架固定金属块调至合适高度，启动变频电机，将金属块调整到与转盘接触，直到出现明显稳定的局部碰摩现象后，开始采集1 min数据并进行全波形记录。虽实验模拟局部碰摩，但实验结果对全周碰摩同样具有指导意义。因为声发射检测机理与振动检测机理区别在于声发射是由材料局部损伤(碰摩)产生的高频应力波，只要有碰摩，无论何种类型碰摩，均会产生声发射现象;而振动监测则是由碰摩产生的冲击，改变了转子原有振型，使转子系统振动频率发生改变，但全周碰摩后，转子与静子持续碰摩，会导致转子系统振动频率无固定规律，导致振动检测困难，本文认为声发射技术能弥补振动检测对全周碰摩检测的局限性。

2.2 数据分析

数据分析过程为在时域及频域对声发射信号进行详细划分，在不同时频域尺度内找到声发射信号特征与转子碰摩特征的稳定联系。具体数据处理流程见图4。

图4 声发射信号处理流程图Fig.4 AE signal processing flow chat

2.2.1 声发射信号波形与功率谱

声发射信号波形与功率谱虽含声发射信号的全部信息，但声发射传感器灵敏度高，可检测出物体表面10-13m甚至10-14m数量级的微小位移。声发射信号本身波形复杂，为短时瞬态信号，较易受多种噪声干扰。图5为碰摩声发射信号波形及功率谱。图5(a)为在600 r/min转速下，传感器1接收的转子碰摩声发射信号，从图中可看出信号峰值为10.99 mv，无法得出更多信息。由图5(b)的功率谱图中可看到瞬态声发射信号在不同频率范围内的能量分布，功率谱峰值为242 kHz，20 dB，功率谱图形同样复杂，从单个信号功率谱图上难以看出声发射信号特征。故需对声发射信号做进一步处理。

图5 碰摩声发射信号波形和功率谱Fig.5 AE waveform and power spectrum of rotor rubbing

2.2.2 小波尺度声发射信号

小波变换可在不同尺度下提取信号的频率与幅值的细节特征，方便研究瞬态信号不同频段内的时频分布状况。图6为小波变换处理声发射信号流程图。

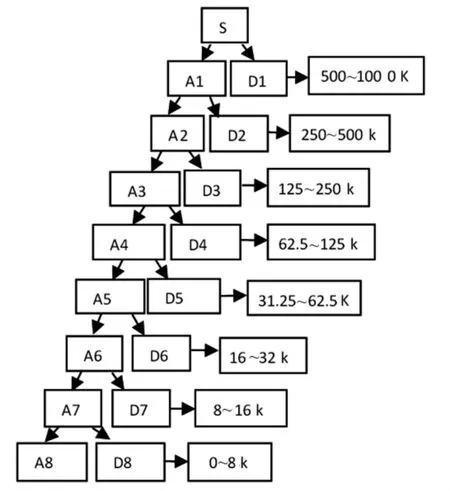
图6 小波处理信号流程图Fig.6 Wavelet signal processing flow chat

图6中分别列举出不同尺度条件下声发射信号代表频段。由于声发射传感器频率范围为100～1 000 kHz，故D5～D8尺度范围内分解的声发射信号无意义。图7为重构声发射信号波形与功率谱。在D4-2尺度条件下，即62.5～500 kHz频率范围内，重构的声发射信号时域波形及对应的功率谱。对比图5(a)看出，重构信号峰值亦为10.99 mv，但由于声发射信号波形复杂，无法从初始波形与重构波形中得出更多有用信息。对比图7(b)、图5(b)可看出，重构后的功率谱峰值相同，均为242 kHz，20 dB;但重构前后功率谱图差别较大，由于经小波变换处理后的功率谱图更注重对原始信号的局部特征进行描述。表明小波变换可将原始声发射信号分解在不同频段范围内，便于研究信号的局部特征。

图7 重构声发射信号波形和功率谱Fig.7 AE waveform and power spectrum of reconstructive signal

表1为不同尺度(D4-1，100～1 000 kHz)的重构声发射信号波形峰值、功率谱频率及峰值。结合图5(b)、图7(b)及表1看出，转子碰摩声发射信号频率主要集中在100～400 kHz，超过500 kHz的D1部分功率谱峰值只占D4-2部分的0.28%。

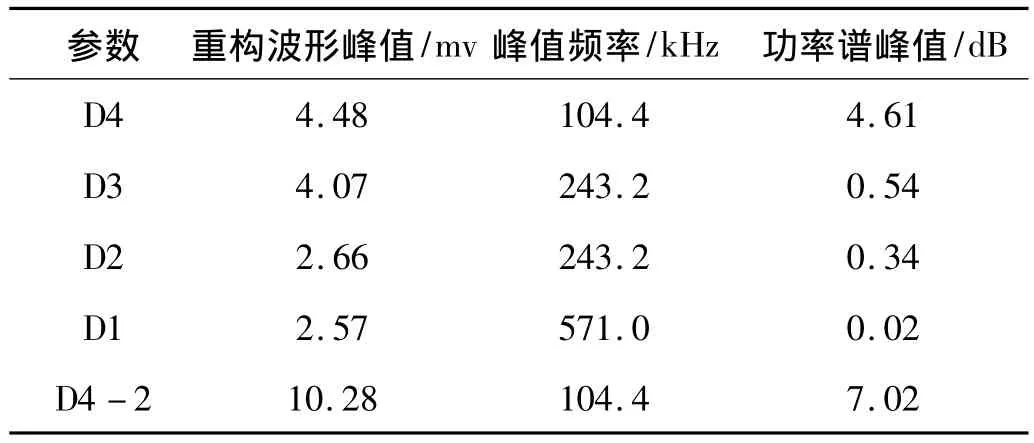
表1 不同尺度声发射信号幅值频率分布Tab.1 Distribution of amplitude and frequency in different wavelet scale

表2为实验过程中初始声发射信号参数统计特征与D4-2尺度下重构声发射信号参数统计特征差值及对应百分比。从表中看出，D4-2尺度下声发射信号平均幅值、峰值频率均与初始发射信号参数基本一致，且二者幅值、峰值频率均较接近。但平均能量相差较多。重构的平均能量不能很好反应损伤状况，原因为声发射传感器过于灵敏，平均能量受门槛影响较大。实验中对100～200 kHz，200～300 kHz频带内声发射信号进行统计分析，结果与100～1000 kHz内统计结果相差30%以上。表明转子碰摩声发射信号能量集中在100～400 kHz频率范围内。

表2 声发射原始信号与D4－2尺度重构信号差值Tab.2 Difference between initial signal and the reconstructive by wavelet in D4 －2 scale

2.3 碰摩声发射信号幅值特征

表3为不同条件下接收的声发射信号差值。从表3看出，相同转速条件下(分别为600 r/min，1 200 r/min)，传感器1接收的声发射信号较传感器2接收声发射信号的平均峰值、平均能量略小，因为碰摩位置距传感器1较传感器2远36 mm;在不同转速条件下(分别为600 r/min，1 200 r/min)，传感器 1、2 接收的声发射信号平均幅值、平均能量均会增加。表明通过声发射信号平均幅值、平均能量可判断转子碰摩位置及程度。

2.4 碰摩声发射信号频率特征

由表3，600 r/min转速下传感器1、2接收的声发射信号峰值频率相差64.53 kHz，而在1 200 r/min转速下相差62.34 kHz。不同检测位置所检声发射信号峰值频率差别较大。传感器1在600 r/min及1 200 r/min转速下接收的声发射信号峰值频率相差5.66 kHz，传感器2相差3.48 kHz。所有声发射信号峰值均在105～125 kHz之间。由数据看出，声发射信号峰值频率随转速增加变化不大，故可通过峰值频率变化判定转子碰摩的相对位置。

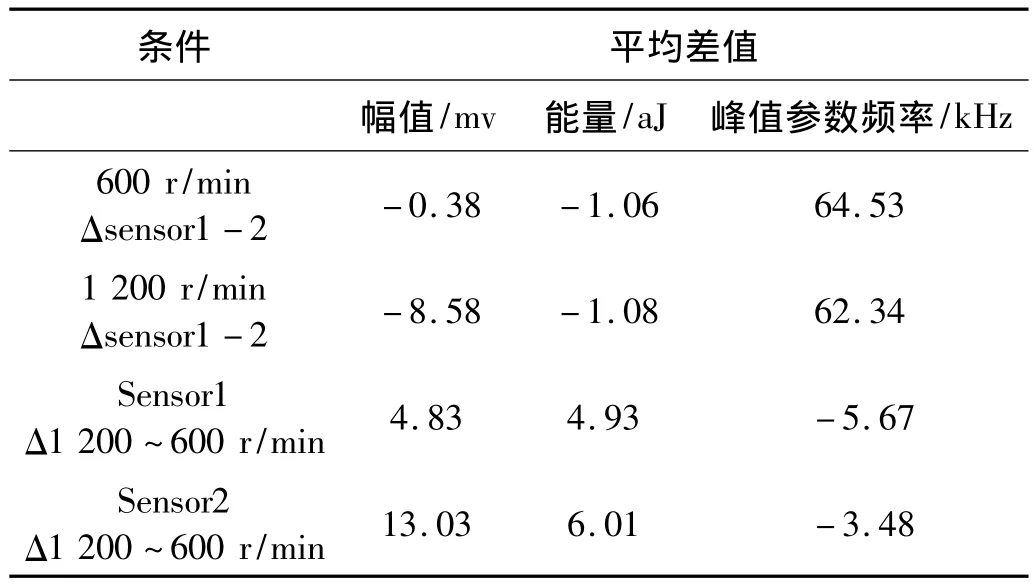
表3 不同条件下声发射信号差值Tab.3 Difference between the AE signal under different conditions

3 结论

(1)声发射检测对转子碰摩较敏感，能有效检测出转子碰摩早期损伤。据碰摩声发射信号特征可判定声发射检测对转子的局部碰摩与全周碰摩同样有效。

(2)小波变换能有效提取声发射信号的局部时频特征，转子碰摩声发射信号频谱范围100～400 kHz，声发射信号参数的平均峰值、平均能量能反映转子碰摩剧烈程度，可作为判定转子碰摩程度依据。

(3)随着转速增加，声发射信号平均峰值、平均能量均会增加。声发射信号峰值频率几乎不随转速变化而变化，却随声发射信号的传播路径而发生变化。因此可利用峰值频率对碰摩位置进行定位。

［1］张 超，韩 璞，唐贵基.基于光滑支持向量回归的旋转机械动静碰摩故障分析［J］.中国工程机械学报，2008，6(1):84-89.

ZHANG Chao，HAN Pu，TANG Gui-ji.Fault analysis on rotor-to-stator rub-impact for rotary machinery using smooth support vector regression［J］.Chinese Journal of Construction Machinery，2008，6(1):84-89.

［2］张占一，刘 杰，应怀樵，等.基于声振信号EMD分解的轻微碰摩故障诊断方法研究［J］.振动与冲击，2009，28(8):91-93.

ZHANG Zhan-yi，LIU Jie，YING Huai-qiao，et al.Research on minor rub-impact fault diagnosis methods based on EMD of vibro-acoustic signals［J］.Journal of Vibration and Shock，2009，28(8):91-93.

［3］徐尉南，张 文，许 斌.柔性转子-柔性静子系统的同步全周碰摩分析［J］.振动与冲击，2007，26(2):1-5.

XU Wei-nan，ZHANG Wen，XU Bin.Analytical study of synchronous full annular rub motion of flexible stator and rotor system［J］.Journal of Vibration and Shock，2007，26(2):1-5.

［4］孟传民，邓艾东，蒋 章，等.转子碰摩故障的声发射与振动特征分析［J］.汽轮机技术，2010，52(6):443-446.

MENG Chuan-min，DENG Ai-dong，JIANG Zhang，et al.Experimental analysis of characteristic of AE and vibration in rotor rub-impact fault［J］. Turbine Technology，2010，52(6):443-446.

［5］Mba D.Applicability of acoustic emissions to monitoring the mechanical integrity of bolted structures in low speed rotating machinery:case study［J］.NDT＆E International，2002，35(5):293-300.

［6］邓艾东，包永强，赵 力.基于高斯混合模型的转子碰摩声发射识别方法［J］.机械工程学报，2010，46(15):52-58.

DENG Ai-dong，BAO Yong-qiang，ZHAO Li.Rub-impact acoustic emission signal recognition of rotating machinery based on gaussian mixture model［J］.Journal of Mechanical Engineering，2010，46(15):52-58.

［7］Kim Y H，Tan A C C，Yang B S.Parameter comparison of acoustic emission signals for condition monitoring of low-speed bearing［J］.Journal of Mechanical Engineering，2008，6(1):45-51.

［8］Douglas R M，Beugn S，Jenkins M D，et al.Monitoring of gas turbine operating parameters using acoustic emission［C］.26th European Conference on Acoustic Emission Testing，Berlin Germany，2004:389-396.

［9］ Mirhadizadeh S A，Moncholi E P，Mba D.Influence of operational variables in a hydrodynamic bearing on the generation of acoustic emission［J］.Tribology International，2010，43(9):1760-1767.

［10］Hall L D，Mba D.Acoustic emissions diagnosis of rotor-stator rubs using the KS statistic［J］.Mechanical Systems and Signal Processing，2004，18(4):849-868.

［11］ Leahy M，Mba D，Cooper P，et al.Acoustic emission for the detection of shaft-to-seal rubbing in large power generation turbines［J］.Advanced Materials Research，2006，13-14:433-438.

［12］邓艾东，童 航，张如洋，等.基于模态分析的转子碰摩声发射特征［J］.东南大学学报(自然科学版)，2010，40(6):1232-1237.

DENG Ai-dong，TONG Hang，ZHANG Ru-yang，et al.Characteristics of rub-impact AE signals in rotating machinery based on modal analysis［J］.Journal of Southeast University(Natural Science Edition)，2010，40(6):1232-1237.

［13］成新民，胡 峰，邓艾东，等.基于代数网络和混沌参数的碰摩声发射源定位方法研究［J］.振动工程学报，2011，24(3):287-293.

CHENG Xin-min， HU Feng， DENG Ai-dong， etal.Research on localization of acoustic emission source based on algebraic neural network and chaotic features［J］.Journal of Vibration Engineering，2011，24(3):287-293.

［14］ Mba D.The use of acoustic emission for estimation of bearing defect size［J］.Journal of Failure Analysis and Prevention，2008，8(2):188-192.

［15］孙延奎.小波分析及其应用［M］.北京:机械工业出版社，2005:59-66.

［16］ Majeed M A，Murthy C R L.A model with nonzero rise time for AE signals［J］.Sādhanā，2001，26(5):465-474.