分数导数黏弹性准饱和土中球空腔振动特性

杨 骁，闻敏杰，高华喜

(1.上海大学 土木系，上海 200072;2.浙江海洋学院 船舶与建筑工程学院，浙江 舟山 316004)

自然土体由固液气三相介质组成。当土中孔隙全部被水充满时，则为饱和土。饱和土中球空腔动力响应研究已取得不少成果。陈仁朋等［1］研究了饱和土中球空腔稳态振动特性，并分析了其在基桩振动中的应用;此基础上，徐长节等［2-3］采用经典 Kelvin本构模型，得到了黏弹性饱和土中球空腔的瞬态响应;以均匀受压球空腔为例，比较了饱和土和单相介质中球面波的传播特性。

严格地来说，自然界中绝对饱和的土是不存在的，相对于饱和土来说，准饱和土更为普遍存在，即孔隙中少量气体以气泡形式包含于水中［4］。Anderson等［5-6］通过含气土试验研究，发现气泡自身会产生振动效应，并影响土体的压缩性、渗透性等性质;之后一些学者又以交通荷载等为例，分析饱和度对瑞利波传播特性的影响［7-9］。然而，对于准饱和土中球空腔动力响应研究较少。徐长节等［10］在Laplace变换域内得到了弹性准饱和土中球空腔动力响应的解析解。在此基础上又采用经典Kelvin模型描述了土体的粘性［11］。上述仅考虑了边界自由渗透或不渗透两种特殊情况，也忽略了衬砌的影响。梁尧箎［12］提出了渗流场的形成与衬砌和土体的渗透系数有关，当衬砌材料渗透系数小于土体的渗透系数时，全部水头由衬砌(介质)承担;当两者相等时，渗流场均匀分布;当衬砌渗透系数大于土体的渗透系数时，全部水头由孔隙水承担。Li［13］以隧道工程为例，提出了绝大部分隧道不单是透水或不透水，而是处于半封闭状态的观点。

另外，与经典微分型和积分型黏弹性本构关系相比，分数导数本构模型可在较宽的频率范围内拟合材料的力学性能和行为，而且具有模型简单及确定模型所需要实验参数少的优点［14-15］。近年来，在岩土工程领域得到了深入研究［16-18］，而在描述准饱和土力学行为方面还未见相关报道。

本文基于Biot两相动力固结理论，将衬砌和土骨架分别视为多孔柔性材料和具有分数导数本构关系的黏弹性体，在频率域内得到了简谐轴对称荷载和流体压力作用下分数导数黏弹性饱和土中球空腔稳态振动时准饱和土的位移、应力和孔压解析表达式。利用界面处衬砌中的流量与准饱和土中孔隙水流量相等，建立了球空腔边界部分透水条件。根据连续性条件，求得了待定系数的表达式，并考察了相对渗透系数、分数导数阶数、材料参数、饱和度等对动力响应的影响。

1 数学模型

如图1，球空腔衬砌内径为R1，外径为R2;而衬砌厚度d=R2-R1。衬砌边界分别作用圆频率为ω的轴对称荷载qseiωt(i2=-1)和流体压力qFeiωt(i2=-1);由于衬砌厚度远小于球空腔半径，设荷载或流体压力无论作用在衬砌内边界还是外边界结果无任何区别［19］。假设衬砌为多孔柔性材料(EL→0)，记球空腔衬砌外边界水头为P2，而内边界水头为P1，并忽略衬砌中孔隙水的影响。

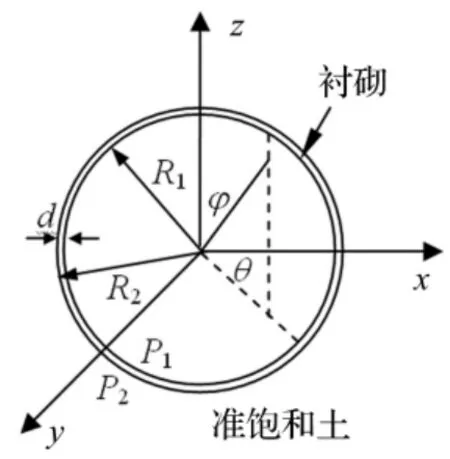
图1 黏弹性准饱和土中球空腔模型Fig.1 Model of spherical cavity in nearly viscoelastic soil

2 分数导数黏弹性准饱和土控制方程

由于准饱和土中气体以气泡形式存在于水中，故可将水-气混合物等价为一种均匀的流体，采用两相孔隙介质理论来模拟准饱和土［20］。根据Biot两相动力固结理论，可知土体的动力方程［21］

总应力σST可表示为:

分数导数模型描述的土骨架应力—应变本构关系用张量表示为［17］:

式中，σSE为有效应力张量;λS，μS，和为土骨架材料参数，λS=2νSμS/(1-2νS)，νS为土颗粒泊松比;且0＜α＜1，Dα=dα/dtα为α阶黎曼—刘维尔分数阶导数，定义为:

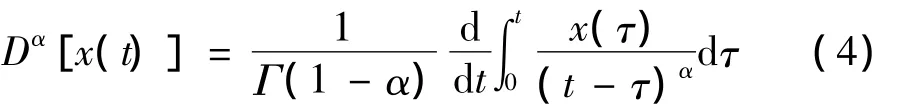
从式(3)中看出，当 α=0或 τσ=τε=0时，该模型退化为经典弹性模型;而当α=1时，该模型可退化为标准线性固体模型。

土骨架应变-位移本构关系可用张量表示为:

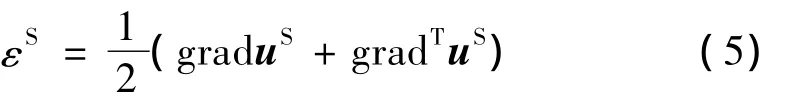
根据Biot动力固结理论，孔隙水压力满足如下本构关系:

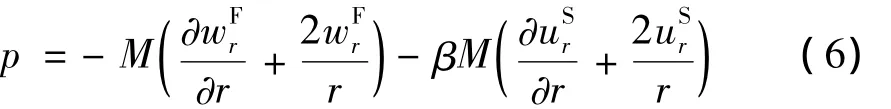
式中，β，M分别表示土骨架和孔隙流体的压缩性系数，可表示为［10］

式中，Ks，Kb，Kf分别表示土颗粒、土骨架和孔隙流体的体积模量。

孔隙流体的体积模量Kf可近似的表示为:

式中，Kw为孔隙水的体积模量;而p0为绝对孔隙压力。从式(8)看出，由于绝对孔压很小，土体中气体含量对孔隙流体的体积模量影响较大。

孔隙流体运动方程为:

式中，b=nρFg/kd为土骨架和流体相互作用系数;kd为动力渗透系数。

结合式(1)～式(3)及式(5)和式(6)，可得到:

再将式(6)代入式(9)，解得:

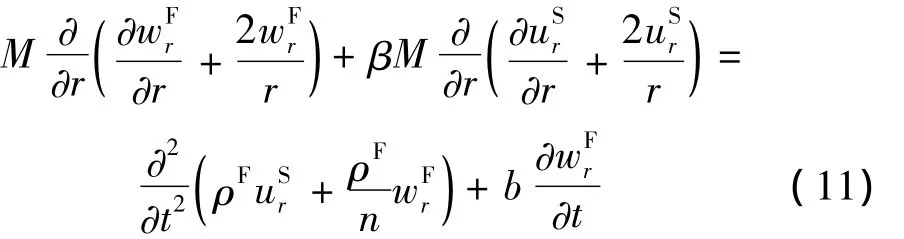
为了求解用位移表示的土体控制方程式(10)和式(11)，引入如下位移势函数:

对于稳态振动，设:

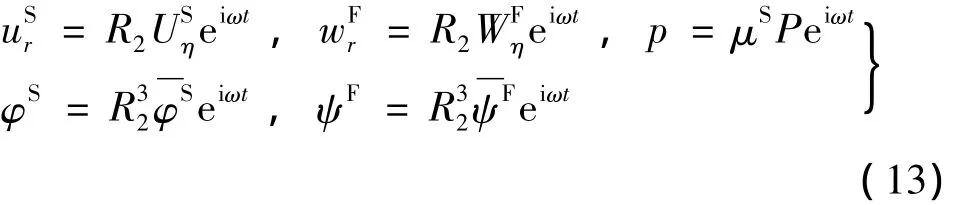
同时，引入无量纲量和常量

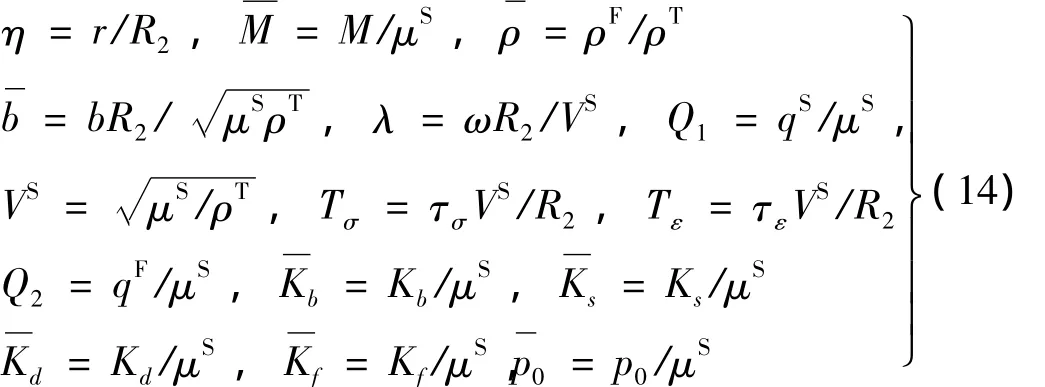
于是，将式(12)～式(14)代入式(10)和式(11)后，可整理得

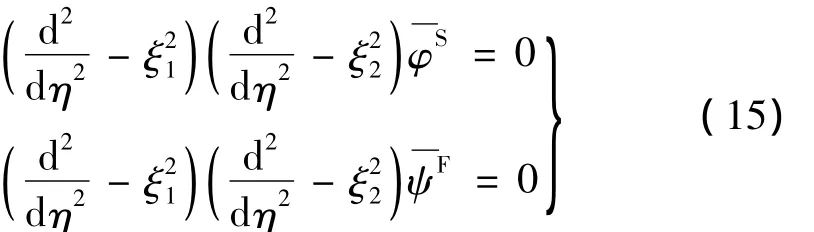
式中:

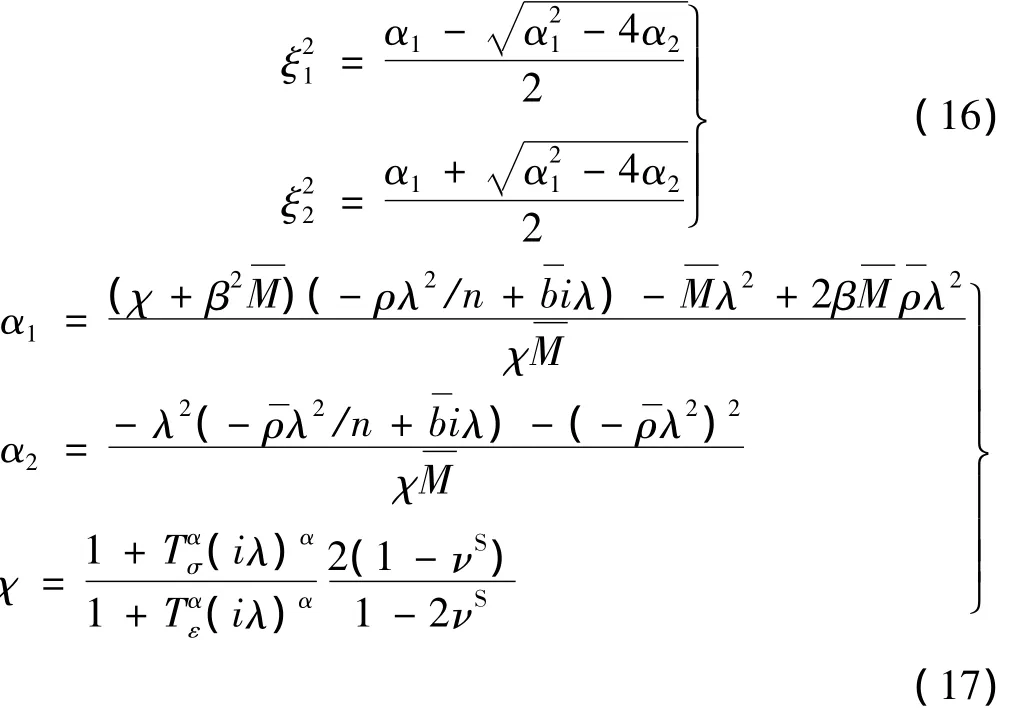
由式(15)可分解得:

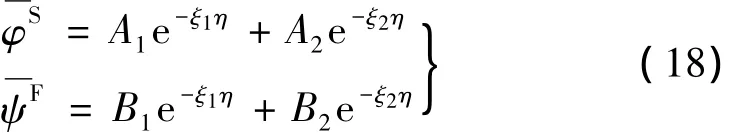
这里，要求 Re(δi)＞0(i=1，2)，且Ai和Bi(i=1，2)为待定系数。

将式(18)代入式(15)，可得到以下关系式

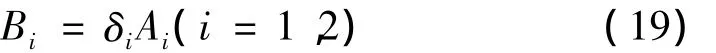
式中，

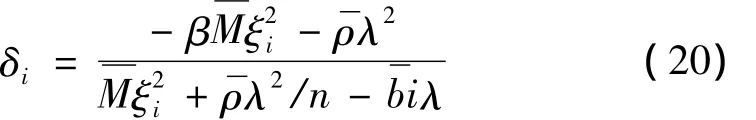
由位移势函数式(12)和式(18)，得:

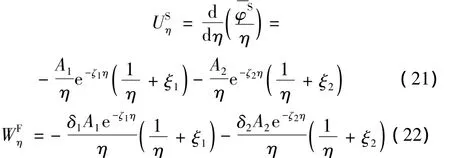
再由式(21)和(22)代入孔隙水压力满足的本构关系(6)，得:

于是，由本构关系(3)和式(21)、式(22)，可得土骨架有效应力为:

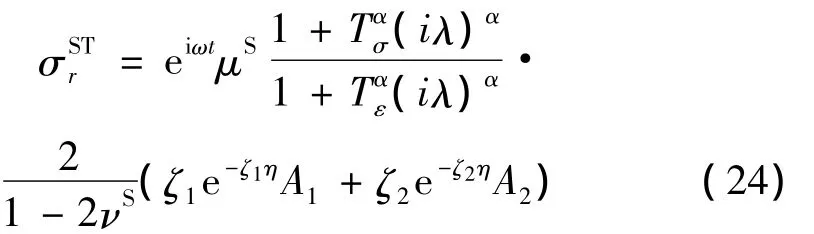
显然，由有效应力算式(2)和式(3)可得到土体总应力为:

式中，

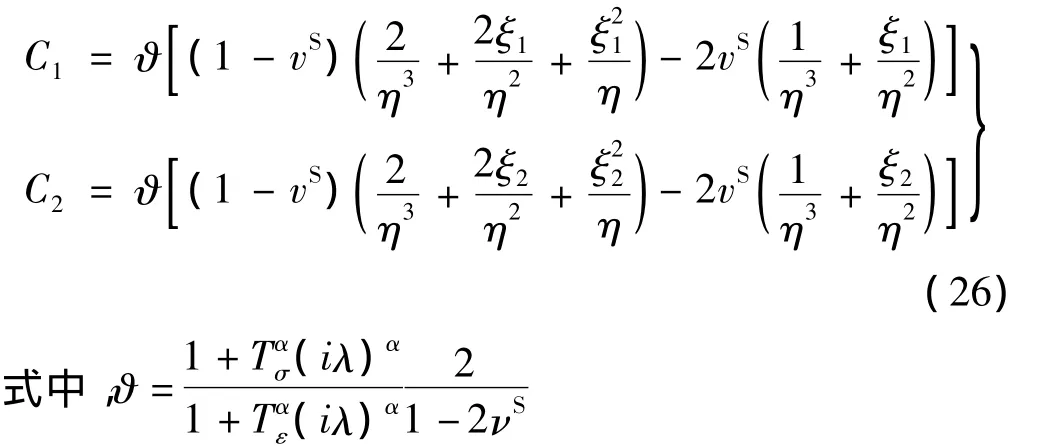
3 边界条件

首先，来确定简谐轴对称荷载qSeiωt(i2=-1)作用下的边界条件。由于多孔柔性衬砌(EL→0)的厚度远小于球空腔半径大小，故假设荷载无论作用在衬砌内边界还是外边界无任何区别。为此，应力协调条件为

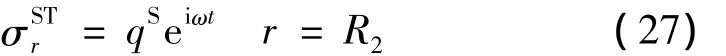
假设衬砌不产生变形，且衬砌和土体紧密接触，忽略衬砌中孔隙流体的影响，利用Darcy渗透定律可得衬砌中的流量［13］

式中，vl为流量;kL为动力渗透系数;γw为流体重度。

然而，准饱和黏弹性土中孔隙水的流量为:

由此，可得P2=p，P1=0，利用界面处(r=R2)饱和黏弹性土中流量和衬砌中水的流量相等［13］，得:

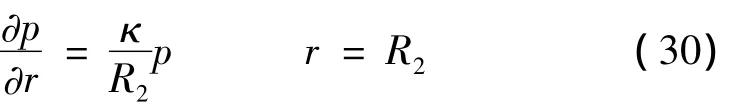
式中，κ=kL/kd(lnR2-lnR2)由衬砌和土体相对渗透系数和衬砌的几何尺寸决定。当kL≪kd时，κ→0，边界不渗透，衬砌处于封闭状态;当kL≫kd时，κ→∞，边界为自由渗透，衬砌为不封闭状态。

再次，确定流体压力作用qFeiωt(i2=-1)下的边界条件。假设在边界应力初始释放，则流体压力全部由孔隙水承担:

同理，得到界面处准饱和土中水头以及衬砌中的水头为P2=p，P1=qFeiωt。由此:

因此，利用边界条件式(27)、(30)及式(31)和(32)，可得分数导数黏弹性土中球空腔稳态响应的解析解。

4 对比分析

［11，17］取值:

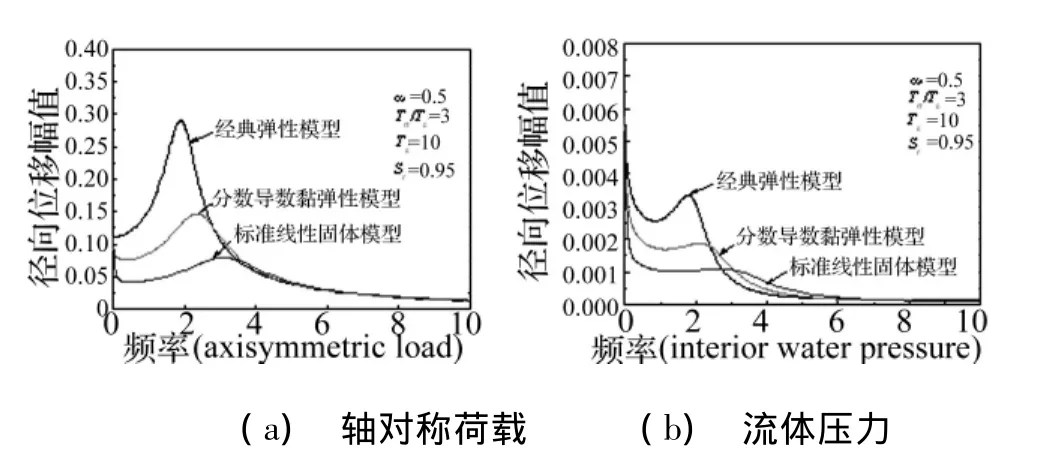
图2 三种模型比较分析Fig.2 Comparative analysis of three models

5 计算结果分析与讨论

下面分析相对渗透系数κ、分数导数阶数α、材料参数比Tσ/Tε和饱和度Sr对黏弹性准饱和土中球空腔振动特性的影响。按式(33)取值。

计算过程中定义位移、应力和孔压幅值为:

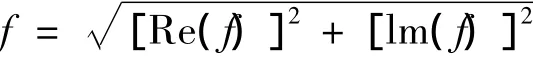
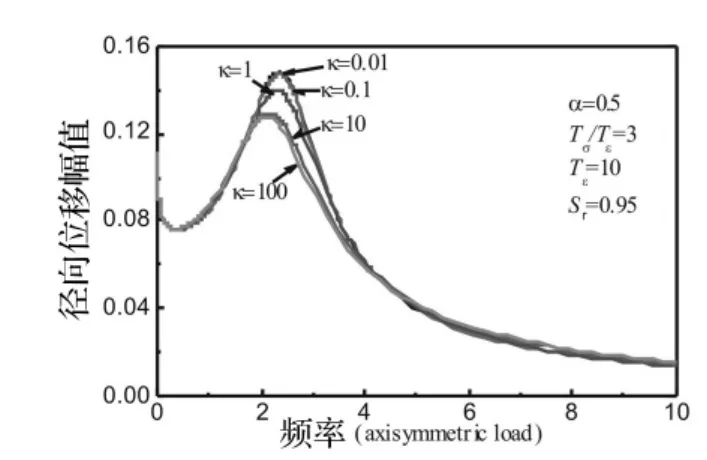
图3 渗透系数κ对径向位移幅值的影响Fig.3 Influence of the permeability coefficient κ on the radial displacement amplitude

图4 阶数α对径向位移幅值的影响Fig.4 Influence of the order α on the radial displacement amplitude

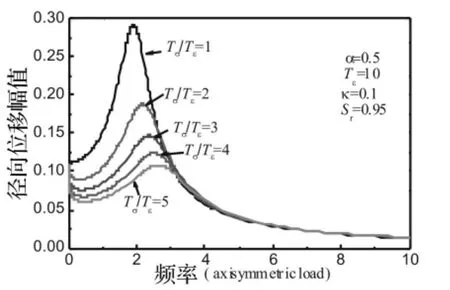
图5 材料参数比Tσ/Tε对径向位移幅值的影响Fig.5 Influence of the material parameter Tσ/Tεon the radial displacement amplitude

首先来考察简谐轴对称荷载作用下物性和几何参数对径向位移幅值和孔隙水压力幅值的影响。图3表示在η=1.5处衬砌和土体相对渗透系数κ对径向位移幅值的影响。可见，随着渗透系数的增加，位移幅值逐渐减小。从中发现当渗透系数κ=0.1和κ=0.01时对位移幅值几乎无任何影响，这表明当κ=0.1时，空腔边界已经接近不透水状态(κ→0);而当κ=10和κ=100时位移幅值几乎无变化，说明空腔边界已经接近透水状态(κ→∞)。渗透系数更精确地描述了球空腔的渗透特性。图4表示分数导数阶数α对径向位移幅值的影响。可见，随着阶数的增加，位移幅值逐渐减小，共振效应减弱。由于分数导数阶数的确定受试验数据和土体外界环境影响较大。因此，可以通过改变其值来拟合试验数据。图5为材料参数比Tσ/Tε对径向位移幅值的影响。从图中看出，随着Tσ/Tε的增加，径向位移幅值的峰值逐渐减小。这是由于Tσ/Tε较大时，准饱和土的阻尼越大所导致的。图5-图7分别表示饱和度对径向位移幅值、径向应力幅值和孔压幅值的影响。可见，饱和度对孔压幅值的影响远大于对径向位移幅值和径向应力幅值的影响。图6可见，准饱和土时的位移幅值峰值大于饱和土时位移幅值的峰值。但在稳态振动时，对于准饱和土来说，饱和度对位移幅值影响几乎相同。从图7发现准饱和土的径向应力幅值峰值比饱和土的径向应力幅值的峰值要大，但衰减的要快。图8可见，饱和土的孔压幅值远大于准饱和土的孔压幅值，这是由于当饱和土时，孔隙水充满整个孔隙，造成孔压较大。因此，将土体视为饱和多孔介质过高地估算了孔压幅值。

下面来考察流体压力作用下物性和几何参数对径向位移幅值和孔隙水压力幅值的影响。图9表示在η=1.5处衬砌和土体相对渗透系数κ对径向位移幅值的影响。可见，流体压力作用下渗透系数对位移幅值的影响与简谐轴对称荷载作用下的影响差异很大。随着渗透系数的增加，位移幅值反而增大。当κ=0.01时即边界接近不透水(κ→0)，位移幅值几乎为零。这是因为初始应力释放，球空腔流体压力全部由孔隙水承担所引起的。图10为分数导数阶数对径向位移幅值的影响。随着阶数的增加，位移幅值逐渐减小。可见，分数导数阶数更精确地描述了流体压力作用下准饱和土球空腔振动特性。图11表示材料参数比对径向位移幅值的影响。可见，材料参数比越大，位移幅值越小，这与轴对称荷载作用下有类似的影响。图12～图14表示流体压力作用下饱和度分别对径向位移幅值、应力幅值和孔压幅值的影响。流体压力作用下饱和度对响应幅值的影响相对较小。图12中，准饱和土时的位移幅值比饱和土的位移幅值要大，这是由于准饱和土中有以气泡形式存在的气体所引起的。图13中可见，准饱和土的应力幅值大于饱和土的应力幅值。图14中，准饱和土的孔压幅值反而小于饱和土中的孔压幅值，这是因为饱和土是假设孔隙被水充满所造成的。

图6 饱和度Sr对径向位移幅值的影响Fig.6 Influence of the saturation Sr on the radial displacement amplitude

图7 饱和度Sr对径向应力幅值的影响Fig.7 Influence of the saturation Sr on the radial stress amplitude

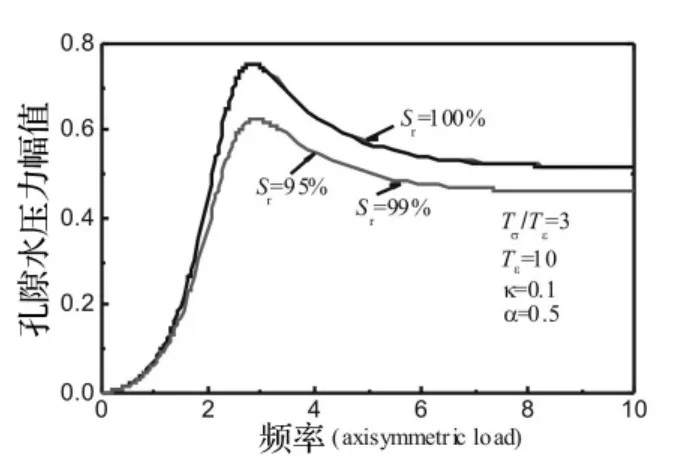
图8 饱和度Sr对孔隙水压力幅值的影响Fig.8 Influence of the saturation Sron the pore water pressure amplitude

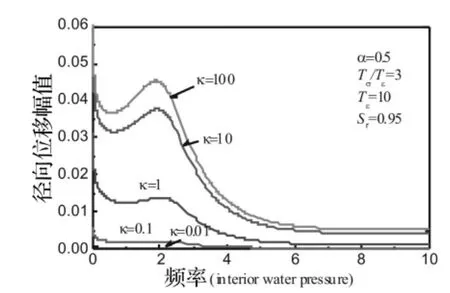
图9 渗透系数κ对径向位移幅值的影响Fig.9 Influence of the permeability coefficient κ on the radial displacement amplitude

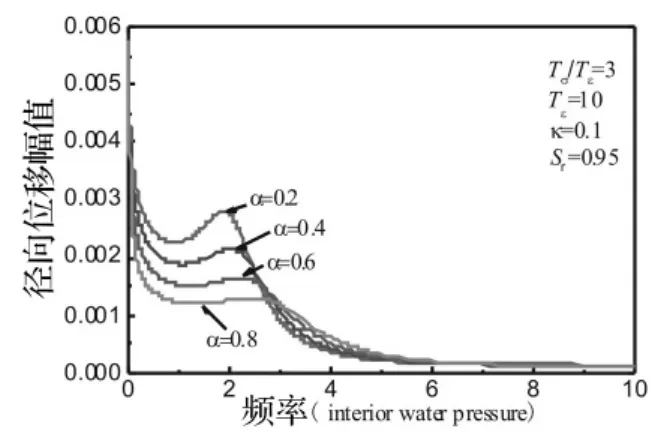
图10 阶数α对径向位移幅值的影响Fig.10 Influence of the order α on the radial displacement amplitude

图11 材料参数比Tσ/Tε对径向位移幅值的影响Fig.11 Influence of the material parameter Tσ/Tεon the radial displacement amplitude

图12 饱和度Sr对径向位移幅值的影响Fig.12 Influence of the saturation Sr on the radial displacement amplitude

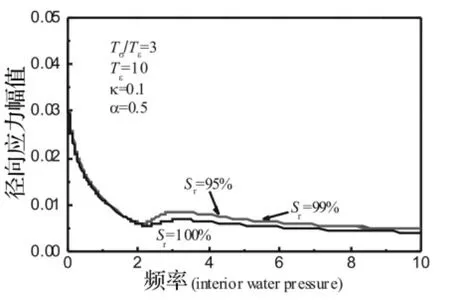
图13 饱和度Sr对径向应力幅值的影响Fig.13 Influence of the saturation Sr on the radial stress amplitude

图14 饱和度Sr对孔隙水压力幅值的影响Fig.14 Influence of the saturation Sr on the pore water pressure amplitude

6 结论

将水—气混合物和土骨架分别视为一种均匀的流体和具有分数阶导数本构关系的黏弹性体，采用Biot两相孔隙介质理论来模拟准饱和土，在频率域内得到了简谐轴对称荷载或流体压力作用下准饱和土中球空腔稳态振动时位移、应力和孔压表达式，考察了物性和几何参数对动力响应的影响，得到如下结论:

(1)简谐轴对称荷载和流体压力两种情况时，相对渗透系数κ对准饱和土中球空腔的动力响应影响很大。轴对称荷载时，随着渗透系数的增加，动力响应减小，而流体压力时随着渗透系数增加，反而动力响应反而增大。

(2)随着分数导数阶数的增加，共振效应明显减弱。由此可见，分数导数本构模型更精确地反映了球空腔的振动特性。通过改变模型参数可以更好地描述土体的力学行为。

(3)随着材料参数比的增加，由于土体的阻抗增大，动力响应明显减小。

(4)轴对称荷载时，饱和度对动力响应的影响比流体压力作用下饱和度对动力响应影响较大。

参考文献

［1］陈仁朋，陈云敏，宣伟丽，等.饱和土中球形空腔稳态振动及其在基桩中的应用［J］.振动工程学报，1998，11(3):373-377.

CHEN Ren-peng，CHEN Yun-min，XUAN Wei-li，et al.Dynamic response of a spherical cavity in saturated soil and its application to piles［J］.Journal of Vibration Engineering，1998，11(3):373-377.

［2］徐长节，蔡袁强.粘弹性饱和土中球空腔的动力响应［J］.土木工程学报，2001，34(4):88-92.

XU Chang-jie， CAIYuan-qiang. Dynamicresponseof spherical cavity in viscoelastic saturated soils［J］.China Civil Engineering Journal，2001，34(4):88-92.

［3］徐长节，吴世明.饱和土中球面波的传播［J］.应用数学和力学学报，1998，19(3):223-231.

XU Chang-jie，WU Shi-ming.Spherical wave propagation in saturated soils［J］.Applied Mathematics and Mechanics，1998，19(3):223-231.

［4］周洪峰，朱陆明，徐长节，等.准饱和土地基刚性基础的竖向振动分析［J］.哈尔滨工业大学学报，2006，38(4):605-608.

ZHOU Hong-feng，ZHU Lu-ming，XU Chang-jie，et al.Vertical vibration of a rigid foundation on nearly saturated soil［J］.Journal of Harbin Institute of Technology，2006，38(4):605-608.

［5］Anderson A L，Hamton L D.Acoustics of gas-bearing sediments I.Background［J］.Acoustical society of America，1980，67(6):1865-1889.

［6］Anderson A L，Hamton L D.Acoustics of gas-bearing sediments II.Measurements and models［J］.Acoustical society of America，1980，67(6):1865-1889.

［7］Bardet J P，Sayed H.Velocity and attenuation of compressional waves in nearly saturated soils［J］.Soil Dynamics and Earthquake Engineering，1993，12(7):391-401.

［8］徐 平，夏唐代，闫东明.平面P1波入射下饱和度对深埋圆形衬砌动应力集中因子的影响［J］.振动与冲击，2007，26(4):46-49.

XU Ping，XIA Tang-dai，YAN Dong-ming.Influence of saturation level on dynamic stress concentration factor of a deeply-buried circular lining caused by an incident plane P1 wave［J］.Journal of Vibration and Shock，2007，26(4):46-49.

［9］王 洁，陈汉良，夏唐代.列车行驶随机激励引起周围地面振动响应分析及其应用［J］.振动与冲击，2004，23(1):88-90.

WANG Jie，CHEN Han-liang，XIA Tang-dai.Analysis of ground vibration under random excitation induced by passing train its application［J］.Journal of Vibration and Shock，2004，23(1):88-90.

［10］徐长节，马晓华，蔡袁强.弹性准饱和土中球空腔的动力响应［J］.岩土工程学报，2005，27(8):934-938.

XU Chang-jie，MA Xiao-hua，CAI Yuan-qing.Dynamic response of spherical cavity in nearly saturated elastic soils［J］.Chinese Journal of Geotechnical Engineering，2005，27(8):934-938.

［11］徐长节，马晓华.粘弹性准饱和土中球空腔的动力响应［J］.岩土力学，2005，26(8):1189-1194.

XU Chang-jie，MA Xiao-hua.Dynamic response of spherical cavity in nearly saturated viscoelastic soils［J］.Rock and Soil Mechanics，2005，26(8):1189-1194.

［12］梁尧箎.水工隧洞中的渗透动水压力［J］.岩土工程学报，1984，6(1):85-90.

LIANG Yao-chi.Hydrodynamic seepage pressure of hydraulic pressure tunnel［J］.Chinese Journal of Geotechnical，1984，6(1):85-90.

［13］ Li X.Stress and displacement fields around a deep circular tunnel with partial sealing［J］.Computers and Geotechnics，1999，24(2):125-140.

［14］ Bagley R L， Torvik P J. A theoretical basis for the application of fractional calculus to viscoelasticity［J］.Journal of Rheology，1983，27(3):201-210.

［15］刘林超，杨 骁.基于分数导数模型的粘弹性桩振动分析［J］.应用基础科学与工程学报，2009，17(2):303-308.

LIU Lin-chao，YANG Xiao.Dynamic analysis of viscoelastic piles based on fractional derivative model［J］.Journal of Basic Science and Engineering，2009，17(2):303-308.

［16］刘林超，闫启方，孙海忠.软土流变特性的模型研究［J］.岩土力学，2006，27(增刊):214-217.

LIU Lin-chao，YAN Qi-fang ，SUN Hai-zhong.Study on model of rheological property of soft clay［J］.Rock and Soil Mechanics，2006，27(Supp):214-217.

［17］刘林超，闫启方，杨 骁.分数导数粘弹性土层模型中桩基竖向振动特性研究［J］.工程力学，2011，28(8):177-182.

LIU Lin-chao，YAN Qi-fang，YANG Xiao.Vertical vibration of single pile in soil described by fractional derivative viscoelastic model［J］，Engineering Mechanics，2011，28(8):177-182.

［18］何利军，孔令伟，吴文军，等.采用分数阶导数描述软黏土蠕变的模型［J］.岩土力学，2011，32(增刊2):239-244.

HE Li-jun， KONG Li-wei， WU Wen-jun， etal. A description of creep model for soft soil with fractional derivative［J］.Rock and Soil Mechanics，2011，32(Supp.2):239-244.

［19］刘干斌，顿志林，谢康和，等.粘弹性饱和土体中半封闭圆形隧洞的稳态响应分析［J］.中国铁道科学，2004，25(5):78-83.

LIU Gan-bin，DUN Zhi-lin，XIE Kang-he，et al.Steady state response ofa partially sealed circulartunnelin viscoelastic saturated soil［J］.China Railway Science，2004，25(5):78-83.

［20］徐 平，夏唐代.饱和度对准饱和土体中瑞利波传播特性的影响［J］.振动与冲击，2008，27(4):11-14.

XU Ping，XIA Tang-dai.Influence of saturation degree on propagation characteristics ofrayleigh waves in nearly saturated soils［J］.Journal of Vibration and Shock，2008，27(4):11-14.

［21］ Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous media.I.Low frequency range［J］.The Journal of the Acoustical Society of America，1956，28(2):168-178.