垃圾填埋场的地震响应特性分析

帅海乐，冯世进，詹黔花

(1.贵州中建建筑科研设计院有限公司，贵阳 550006;2.同济大学 地下建筑与工程系，上海 200092)

从上个世纪80年代开始，就有学者研究垃圾填埋场的动力特性。由于城市固体垃圾具有多样性、多孔性、高非均质性和各向异性，且性状还随组成物质的腐烂分解过程不断发生变化，使得其静、动力性状很难测定。特别是填埋场实震记录不多，使得其动力响应研究比较缓慢。直到1994年Northridge地震发生后，采集到实震记录，才为填埋场的地震响应分析提供了很好的条件。

垃圾填埋场常用的动力分析方法有以下三种:①拟静力法，是一种基于极限平衡理论方法。Bray［1］认为拟静力法可以用于地震活动不很频繁地区垃圾填埋场的动力反应分析。② 等价线性分析方法，应用最为广泛的是联合极限平衡稳定分析法和动力变形分析法中的一维等价线性动力分析法。Bray［2］应用该法对填埋场地震产生位移的影响因素进行了分析，表明垃圾填埋场稳定不仅与垃圾动力特性有关，而且和填埋高度、场地条件有关。Matasovic［3］对OVSL填埋场的覆盖系统变形及稳定进行了分析并和实震破坏情况作了对比。③非线性分析方法，考虑材料的动力非线性，一般采用粘弹性模型，求解动力方程用等效线性迭代法。陈云敏、柯瀚等［4－5］用二维有限元对杭州某填埋场的地震响应进行了分析。邓学晶［6］用FLAC程序对填埋场地震响应特性进行了二维有限差分分析。Idriss等［7］用二维有限元对填埋场进行了非线性分析。Augello［8－9］对填埋场用 QUAD 程序进行了二维分析。Kavazanjian用二维有限元对OII填埋场的地震记录进行了反分析。Psarropoulos［10］用二维有限元分析了填埋场场地条件对地震响应的影响，表明地基刚度和地震水平对填埋场稳定影响较大。

由于垃圾的动力特性、动荷载、填埋场的规模及场地条件都会影响填埋场的动力响应情况，不同学者侧重点不同，研究得出的结论也有区别。需对垃圾填埋场的动力响应情况进行综合分析找出普适性规律，以便为填埋场的抗震设计及分析提供参考。本文结合现有试验资料，用二维有限元程序对山谷型填埋场进行动力分析，综合考虑了地基刚度、动荷周期、幅值及填埋体的刚度对填埋场顶部加速度响应的影响，得出了其加速度的响应规律，可供填埋场抗震设计参考。

1 垃圾的静、动力特性及分析方法

1.1 静力本构模型

Machado等通过室内试验和现场测试发现垃圾土属加工硬化型材料，其应力应变关系曲线和邓肯—张双曲线模型比较接近。张振营、冯世进等进行试验得出同样结论。静力计算采用割线模量公式:

式中:σ1，σ3为第一、第三主应力;K，n分别为土的模量系数和模量指数;

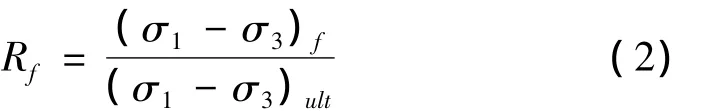
式中:Rf为破坏比;(σ1－σ3)f为破坏时的主应力差;(σ1－σ3)ult为主应力差的渐近值。

1.2 剪切波速

垃圾剪切波速是反映垃圾土动力特征的参数，是垃圾刚度的反映。Kavazanjian通过对加利福利亚南部10个填埋场测试表明填埋场剪切波速随埋深和填埋时间线性增加，浙江大学岩土研究所对杭州某填埋场用SASW法测得其剪切波速范围为80～160 m/s。

剪切波速与土动弹性模量、动剪切模量之间的关系为:

式中:Ed—动弹性模量;ρ—密度;μ—泊松比;Gd—动剪切模量。

1.3 动力本构模型

Matasovic［11］通过试验发现垃圾在循环荷载作用下呈现出明显的滞回圈，可用等效线性模型来描述，用类Hardin-Drnevich模型来描述。

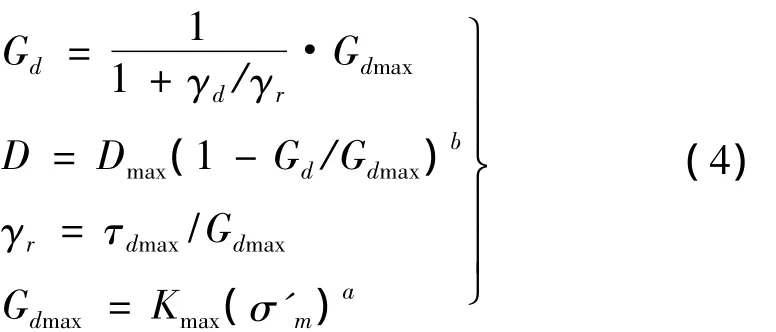
式中:γr为参考剪应变;τdmax为最大动剪应力;K值和a值与垃圾材料有关，可以通过室内小应变或现场剪切波速测定;b值可由试验测得的阻尼曲线拟合得到;Dmax可用材料的阻尼比初始迭代。本文进行动力分析过程中，采用等效线性分析来考虑动力非线性，其剪切模量和阻尼比随动剪应变的变化曲线参照kavazanjian等通过实震记录反演的剪切模量和阻尼变化关系曲线，如图1所示。

图1 垃圾材料剪切模量和阻尼随剪应变关系Fig.1 Modulus reduction and damping curves for MSW

1.4 动力分析有限元方程

以渗流与动力分析相耦合的Biot动力固结方程为基本方程，采用加权余量法，取权函数为形函数得出动力分析的有限元计算分析格式:

式中:［M］为质量矩阵;［C］为总阻尼矩阵;［K］为刚度矩阵;［Q］为耦合矩阵;［H］为渗透矩阵;［F1］、［F2］为荷载矩阵;［A］为位移矩阵。其中，不排水有效应力法和总应力法的计算格式可以从式(6)中退化而得。不排水有效应力动力分析方法假定在地震期间的孔隙水不向外排出，而是封闭在土体骨架中。分析时考虑到地震过程中孔隙水压力的逐渐增长、有效应力不断降低和土的剪切模量随有效应力的降低而减小，不考虑孔隙水压力的消散与扩散的影响。总应力法分析过程中不考虑孔压影响，去掉式(5)中与孔压u有关

式中:［F］为荷载矩阵。

由于填埋体材料和场地材料的动孔压模型参数采取比较困难，本文暂不考虑有地下水影响的情况。

1.5 动力分析方法的实现过程

静力计算初始迭代值，动力分析时材料选用等效线性模型，分时段用Wilson－θ法逐步积分法求解动力方程，采用非线性分析过程，在弹性的迭代中，每个单元记入与应变有关的剪切模量和阻尼比，再求得与应变水平相应的剪切模量和阻尼比，逐步迭代，直至地震结束。的项即可得到该两种方法的动力分析有限元方程:

2 填埋场建模

2.1 填埋场计算模型

根据山谷型填埋场的特征，建立如下图2所示计算模型。其中填埋场高度80 m，底部长度300 m，坡度为1∶3，地基厚度120 m，长度720 m。采用粘滞边界，通过设置阻尼器来吸收传到边界上的波动能量，从而消除或减小在边界上的反射。用Geo-Slope系列软件中的QUAKE/W模块进行静、动力分析。

图2 山谷型垃圾填埋场计算模型Fig.2 Calculation model for valley-type landfill

2.2 计算参数的选取

垃圾材料的静力参数参照张振营等［12］所做试验选取，动力参数参照冯世进［13］做的动三轴试验选取(所配置垃圾材料试样也是参照张振营等试验结果)。地基的静、动力参数选取参照文献［14］给出的典型值，具体见表1。

表1 算例材料基本参数Tab.1 Parameters of example materials

2.3 地震荷载及其输入方法

主要分析填埋场地震响应特性，没有严格按照抗震设计要求选取地震波，选择了一个实际的EL-Centro地震波(简称EL波)和3种不同周期的简谐波(谐波1～3)，其持续时间均选为10 s，EL-Centro地震波(前10 s)的波形见图3。各地震荷载的周期特征见表2。

图3 EL-Centro地震波(EL波)加速度时程Fig.3 EL-Centro Acceleration time histories

表2 填埋场动力响应计算方案Tab.2 Calculation scheme for seismic response analysis of landfill

在输入方法上做了较大改进，先仅建立地基模型，此时地基上无填埋场，在地基底部输入地震荷载，得到地基表面的加速度时程，将其作为已知的地面自由场记录，而把输入的加速度视为“反演”出的加速度，对填埋场响应进行分析时，还是从地基底部输入地震荷载，地基模型不变，这相当于把地基模型对加速度的传播影响做了归零处理，这样能够反映出填埋场对地震荷载响应的解耦处理。

2.4 填埋场地震响应特性分析的计算方案

不考虑地下水的影响，这在覆盖系统、淋滤液排放系统正常工作的情况下适用。考虑场地条件、材料特性及动荷特性对填埋场动力响应的影响，分64种情况进行计算分析，其组合考虑的因素见表2。

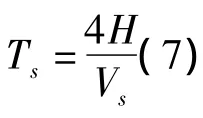
3 计算结果分析

采用抗震设计中通常考虑的加速度响应结果来进行分析，在填埋体中设置如图4所示10个特征点。

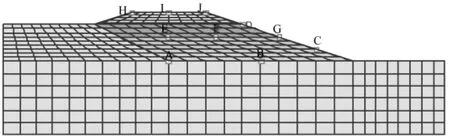
图4 填埋场中特征点设置Fig.4 Feature points of MSW landfill

图5 砂土地基谐波0.12 g谱加速度Fig.5 Acceleration spectrum of I in sand ground with sine wave 1

计算分析结果表明:各特征点在同一模型下，其动力响应情况相似，幅值大小不同，谐波作用时，这种规律更明显。幅值变化情况呈现如下趋势:填埋场顶部的 H、I、J三点，I点幅值介于其它两点之间，A、E、I三点反映出加速度响应随高度的变化，在任何荷载下I点加速度总是得到放大，通常C、G两点的幅值较D点大。选取I点的加速度响应情况来分析填埋场动力响应特性，比较有代表性。

填埋场的响应是在地震荷载作用下，填埋场和地基相互作用的结果。动荷响应特性受地基的基本周期Ts、地震荷载的卓越周期Tp和填埋场的基本周期TL影响很大，各影响因素都可归结为对这三个周期的作用，可通过三者的相互关系来分析各个因素对填埋场的动力响应规律:

(1)当Ts=Tp时，即填埋场地基的基本周期和动荷卓越周期相近时，地基使动荷得到放大，此时可能出现三种情种:当 Tp=TL时，填埋场和地基同时达到共振状态，填埋场顶部的加速度响应达到最大(图5)，这是设计中应该避免的情况;当Tp＜TL时，填埋场的基本周期比地震荷载的卓越周期大，填埋场顶部加速度响应中等，主要是地基对动荷的放大效应(图6);当Tp＞TL时，填埋场的基本周期比地震卓越周期小，但是随着动荷幅值的增大，材料非线性会使填埋材料的剪切模量减少，阻尼增大，填埋场的周期TL增加，有可能使Tp=TL，从而在顶部产生很大的响应(图7中0.36 g)。

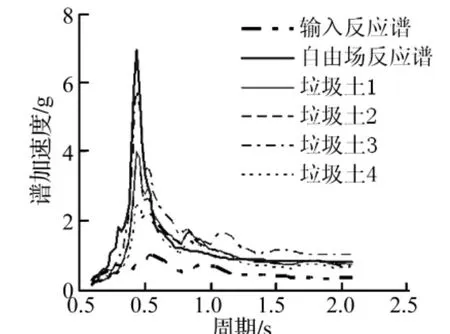
图6 基岩EL地震波0.36 g谱加速度Fig.6 Acceleration spectrum in rock ground with EL seismic wave 0.36 g

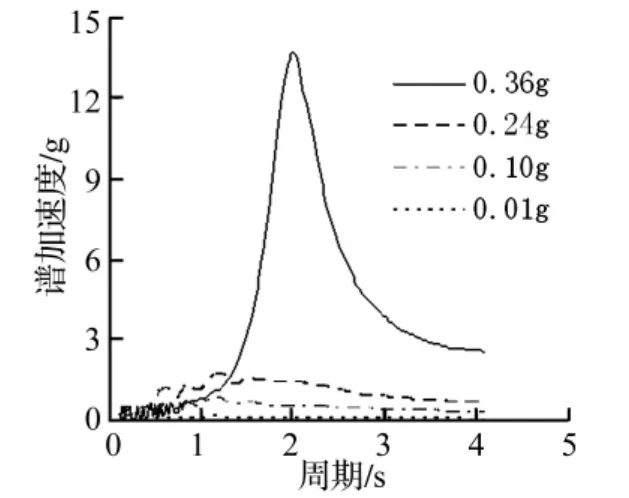
图7 卵石地基谐波1时I点谱加速度Fig.7 Acceleration spectrum of I in pebble ground with sine wave 1

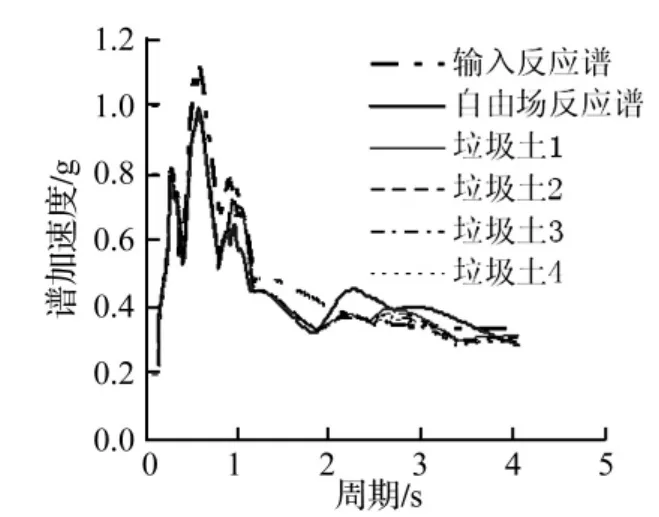
图8 粘土EL地震波幅值0.36 gFig.8 Acceleration spectrum in clay ground with seismic wave 0.36 g

图9 基岩谐波1幅值0.24 g谱加速度Fig.9 Acceleration spectrum of I in rock ground with wine wave 1 0.24 g

图10 卵石EL地震波谱加速度Fig.10 Acceleration spectrum in pebble ground with EL seismic wave

(2)当Ts＞TL时，地基材料的非线只会使地基的基本周期增大，二者周期会相差更大，地基不会产生共振效应，地基对动荷的传播影响不大，如本文中采用的粘土地基模型，这种情况在现实中是比较少见的，在有深厚覆盖的粘土层上修建填埋场时可能会出现这种情况。这时Tp和TL的关系对响应结果影响较小，顶部的响应情况和原来输入动荷基本相同，响应情况比较单一(图8)。

(3)当Ts＜Tp时，地基材料的非线性有可能使得地基的基本周期增大，这时候填埋场的响应可能出现三种情况:当Tp=TL时，填埋场会达到共振状态，这时响应情况主要是受动荷周期的影响较大(图9);当Tp＜TL时，填埋场的基本周期比地震荷载的卓越周期长，由于填埋材料的非线性会使得填埋场的周期变长，这种情况下不会出现较大的响应情况(图10);当Tp＞TL时，填埋场的基本周期比地震的卓越周期小，但是随着动荷幅值的增大，材料非线性会使填埋材料的剪切模量减少，阻尼增大使填埋场的周期TL增大，有可能使Tp=TL，从而在顶部产生很大的响应情况。

(4)通常情况下TL较大，Tp和Ts较小，对于压得很密实或者填埋时间长久的填埋场，剪切波速增加使TL减小，从而容易使周期接近，而激发较大响应。(图6、9、11、12)都反映出垃圾土1、2在地震卓越周期较大时产生响应强烈，而垃圾土3、4在地震的卓越周期小时产生响应强烈，长卓越周期的地震容易激发较大的响应也是由于增大Tp原因。地震幅值的增加，总会由于材料的非线性，使得地基和填埋场基本周期增加(图10、图13、图14)都反映出髙幅值加速度总能在长周期上激发较髙的响应值。小。通常情况下TL较大，Tp和Ts较小，对于压得很密实或者填埋时间长久的填埋场，剪切波速增加使TL减小，从而容易使周期接近，而激发较大响应。地震幅值的增加，由于材料的非线性，使得地基和填埋场基本周期增加，设计中应尽量使三者的周期相差较大。

图11 基岩谐波2幅值0.10 g谱加速度Fig.11 Acceleration spectrum in rock ground with 0.1 g sine wave 2

图12 基岩谐波3幅值0.01 g谱加速度Fig.12 Acceleration spectrum in rock ground with 0.01 g wine wave 3

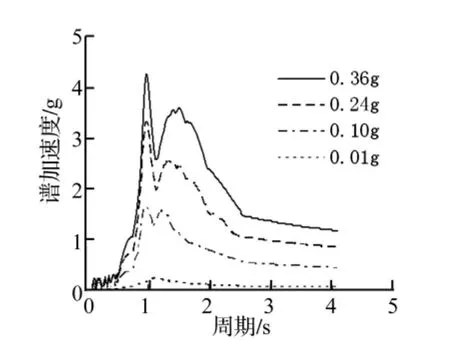
图13 卵石谐波2时I点谱加速度Fig.13 Acceleration spectrum of I in pebble ground with sine wave 2

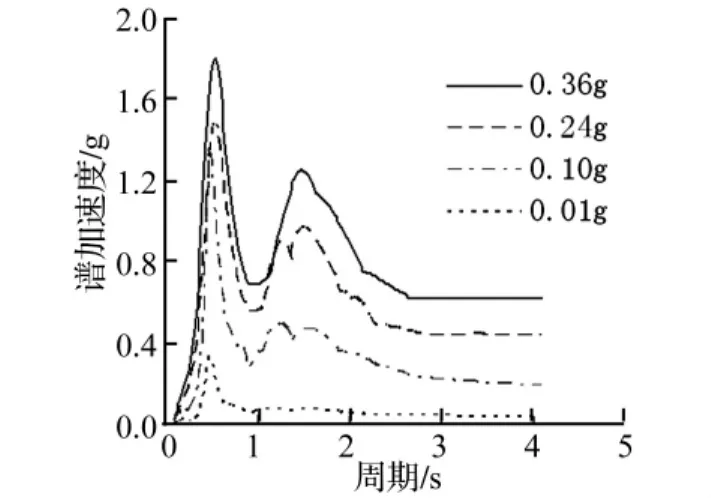
图14 卵石谐波3时I点谱加速度Fig.14 Acceleration spectrum of I in pebble ground with sine wave 3

本文仅用了响应加速度和谱加速度进行分析，有待进一步考虑其它地震响应值的特征，同时验证改变材料刚度和厚度对周期的影响效果是否相同。

4 结论

动荷的响应特性受地基的基本周期Ts、地震卓越周期Tp和填埋场的基本周期TL影响很大。场地条件、材料剪切波速(刚度)、动荷周期和幅值都是通过改变这三个周期的相对大小关系来改变填埋场的响应情况。当Ts=Tp=TL时，填埋场顶部的响应一定达到最大，如果Tp=TL或者Tp=Ts，则填埋场的动力响应值达到中等，三个周期如果相差甚远，填埋场的响应值最

［1］ Bray J D，Augello A J.Seismic stability procedures for solidwaste lanffills［J］.Jouranl of Geotechnical Engineering ASCE ，1995，121(2):139－151.

［2］ Bray J D.Earthquake-Induced displacements of solid waste landfills［J］.Journal of Geotechnical and Geoenvironmental Engineering ASCE ，1998，124(3):242－253.

［3］Matasovic N，Kavazanjian Jr E.Seismic response of a composite landfill Cover［J］.Journal of Geotechnical and Geoenvironmental Engineering ASCE ，2006，132(4):448－455.

［4］陈云敏，柯 瀚，凌道盛.城市垃圾填埋体的动力特性及地震响应［J］.土木工程学报，2002，35(3):66－71.

CHENYun-min， KE Han，LING Dao-sheng.Dynamic properties and seismic response of municipal solid waste［J］.China Civil Engineering Journal，2002，35(3):66 －71.

［5］柯 瀚，陈云敏，等.城市垃圾填埋场地震稳定分析及永久位移计算［J］.地震学报，2001，23(2):204－212.

Ke Han Chen Yunmin，etal. Stabilityand permanet displacements analysis of wasteland during earthquakes［J］.Acta Seismologica Sinica，2001，23(2):204 －212.

［6］邓学晶孔宪京.平原型城市垃圾填埋场的地震响应特性及稳定性评价［C］//第7届全国土动力学学术会议论文集.北京:2006，11.360－365.

［7］Idriss I M，Giegel G.Seismic response of the operating industris landfill［J］.Geotechnical Special Publication No.54 ASCE，367 －379.

［8］Augello A J，Bray J D.Dynamic properties of solid waste based on back-analysis of oII landfill［J］. Journal of Geotechnicaland GeoenvironmentalEngineering ASCE，1998，124(3):211－220.

［9］Augello J A，Bray J D，Leonarda G A.Response of landfills to seismic loading［J］. JournalofGeotechnicaland Geoenvironmental Engineering ASCE，2000，126(2):1051－1061.

［10］ Psarropoulous P N，Tsompanakis Y.Effects of local site conditions on the seismic response of municipal solid waste landfills［J］.Soil Dynamics and Earthquake Engineering，2007，27:553 －563.

［11］ Matasovic N，Kavazanjian Jr E.Cyclic characterization of oII landfill solid waste［J］.JournalofGeotechnicaland Geoenvironmental Engineering ASCE，1998，124(3):197－210.

［12］张振营，吴世明，陈云敏.城市生活垃圾土性参数的室内实验研究［J］.岩土工程学报，2000，22(1):35－39.

ZHANG Zhen-ying， WU Shi-ming， CHEN Yun-ming.Experimental research on the parameter of life rubbish in city［J］.Chinese Journal of Geotechnical Engineerin，2000，22(1):35－39.

［13］冯世进.城市固体废弃物静动力强度特性及填埋场的稳定分析［D］.杭州:浙江大学.2005.

［14］孙 静.岩土动剪切模量及阻尼试验研究［D］.哈尔滨:中国地震工程局力学研究所，2004.