一种针对未知参数系统的实时混沌化方法

周加喜，徐道临，张月英，刘春嵘

(湖南大学 机械与运载工程学院 深海装备研究与开发中心，长沙 410082)

近年来，混沌化(或混沌反控制)越来越被学者所重视，其工程应用已涉及信息加密、宽带通信、溶剂混合以及生命科学等领域［1］。近期Lou等［2］提出当隔振系统处于混沌状态时，将简谐输入转化为宽频输出，有效改变了噪声的线谱特征，提高了水下航行器的隐蔽性。但系统混沌状态敏感地依赖于激励条件和系统参数，当其改变时，混沌很可能随之而消失;而且针对某一激励条件确定的混沌参数对应的隔振系统不能保证其隔振性能。因此，多种方法被用来实现隔振系统的混沌化。

Yu等［3］提出用一种类似于广义混沌同步的方法，用类似达芬系统的混沌信号驱动隔振系统使之处于混沌状态，但该方法似乎仅适用于特定参数。Wen等［4］基于改进的投影混沌同步化方法，利用电系统(达芬系统)驱动隔振系统，使系统处于混沌状态，且隔振性能良好，但该方法需要较大的能量完成控制过程。Liu等［5］提出用反馈控制来实现隔振系统的混沌化，该方法以最大Lyapunov指数为正作为控制目标，但这类控制方法在实时控制中不可行［4］。张振海［6］基于 Konishi［7］的离散反馈控制方法对隔振系统进行了混沌化。该方法通过在时间区间［nT，(n+1)T］对系统积分建立x［(n+1)T］与x(nT)的映射关系，将连续系统离散，然后利用离散时间系统反馈混沌化方法［8］对系统实施混沌化。而时延反馈混沌化方法［9］可以直接对连续时间系统实施混沌化，且研究表明不管线性系统还是非线性系统，都能达到很好的混沌化效果。Xu等［10］也指出时延反馈控制可作为系统状态混沌或非混沌的开关。但是，多数混沌化方法都是针对确定系统，且对系统的动力学特征需分析得十分透彻，而针对未知系统的混沌化研究几乎没有。

本文将基于作者之前的工作［11］，提出一种针对未知参数系统的实时反馈混沌化方法。基于系统稳态响应构造性能指标，量化系统稳态行为(周期或混沌等)，随着时间进程的推进，依照直接寻优算法，调整反馈控制器的时延，直至算法收敛，此时认为性能指标达到最小值，且系统进入最佳混沌状态。本方法最大的优势在于仅仅需要通过数值仿真或试验测试获取系统稳态响应，并构造频谱性能指标来量化系统状态;通过优化时延量来控制频谱特性，将混沌化问题转化为优化问题，跨越了界定混沌参数的传统方法;本方法的实施无需知道系统参数，对于工程实际系统易于实现实时控制。

1 混沌化方法

1.1 理论模型

如前所述隔振系统处于混沌状态可有效控制噪声线谱特征［2］，但针对激励条件，系统混沌参数域是一定的，而具备混沌参数的系统不一定具备隔振性能;而且当激励条件改变时混沌状态会随之而消失。因此，多种控制方法被用来对隔振系统实施混沌化。本文拟采用时延反馈控制，对双层线性隔振系统实施混沌化。双层隔振系统可简化为如图1所示的二自由度质量－弹簧系统。m1，m2分别表示被隔振设备和筏体;k1，k2为线性弹簧;c1，c2为黏性阻尼。在 m1和m2之间安装作动器 u，以实现反馈控制。控制流程亦见图1:采集系统响应，并对信号进行延迟和非线性函数运算处理，进而作为控制信号输入作动器并执行，从而实现时延反馈控制。在简谐激励力和控制器作用下系统的运动方程为:

其中:u(t，τ)为时延反馈控制器。如果系统参数已知，根据Wang和Chen的方法［1］可以推导出控制器的解析表达式;而本文考虑的是未知参数系统，故采取类似形式的控制器:

这种非线性控制器能比较容易实现动力系统的混沌化，但混沌参数区间需要利用分岔分析来界定。当系统参数未知时，混沌参数区间的界定将无从下手。基于我们之前提出的最优时延反馈混沌化概念［11］，跨越寻找混沌参数的传统方法，针对未知系统混沌化提出以下控制策略。

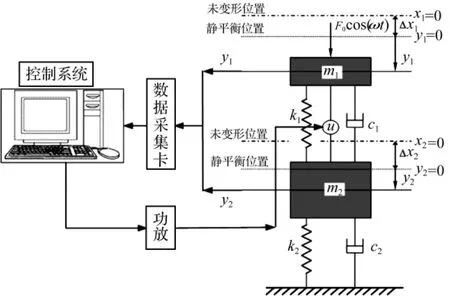
图1 受时延反馈控制的二自由度系统Fig.1 Two DOFs system under time-delay feedback control

1.2 控制策略

核心思想:实时跟踪系统响应，获取一段时间内的稳态响应，并进行快速傅里叶变换(FFT)得到系统响应的幅值谱，然后利用并改造我们之前构造的性能指标［11］，量化系统的动力学行为，混沌行为越明显则性能指标越小。依照Hooke-Jeeves方法［12］，随着时间进程，及时调整控制器的时延，直至性能指标趋近于最小值，则认为系统已处于较好的混沌状态。其流程图如图2所示。

图2 实时最优时延反馈混沌化流程图Fig.2 Flow chart of the optimal time-delay feedback chaotification method

基于数值仿真或实验测试获得的系统响应，性能指标通过如下表达式来构造:

其中:Y为系统响应时间序列di的幅值谱;Ymax，Ymin分别为幅值谱的最大值和最小值;为幅值谱除去前三个最大值后所有幅值的均方根，该值用来衡量响应中谐波或(和)次谐波成分的多少，即用其来近似描述幅值谱的宽度。除去前三个最大值是为了区分拟周期、锁相与混沌。众所周知，宽频连续谱预示着系统响应很可能是混沌的［13］。

在时间历程中，先后取等长的三个时间段ΔTk，ΔTk+1，ΔTk+2，分别施加时延为τj，τj－δ，τj+δ的控制输入，如图3所示。每个时间段ΔT包含三部分:第一部分Td消除瞬态响应;第二部分Ts为稳态响应时间段;考虑到实际控制系统，第三部分Tc为性能指标计算和寻优算法所消耗的时间。性能指标I便是基于第二部分时间段内的稳态响应构造而来。

Hooke-Jeeves方法［12］是一种直接搜索方法，包含探索步和加速步。探索步通过比较τj，τj－δ，τj+δ对应的指标值，确定每个迭代的基点τj+1。如果指标值没有改善则折减探索步增量δ/λ，再进行探索，当δ≤ε时搜索结束。探索步成功找到新基点后，实施加速步。如果指标有所改善，则加速成功，将加速后的点作为基点返回探索步;如果加速失败，则直接回到探索步。控制器时延值每次探索或加速，时间历程按ΔT推进，性能指标不断被改善，直到满足算法的收敛条件，性能指标达到最小值，从而达到混沌化的目标。

图3 寻优时间历程Fig.3 Time process for searching optimal time delay

2 数值算例

表1 系统参数Tab.1 System parameters

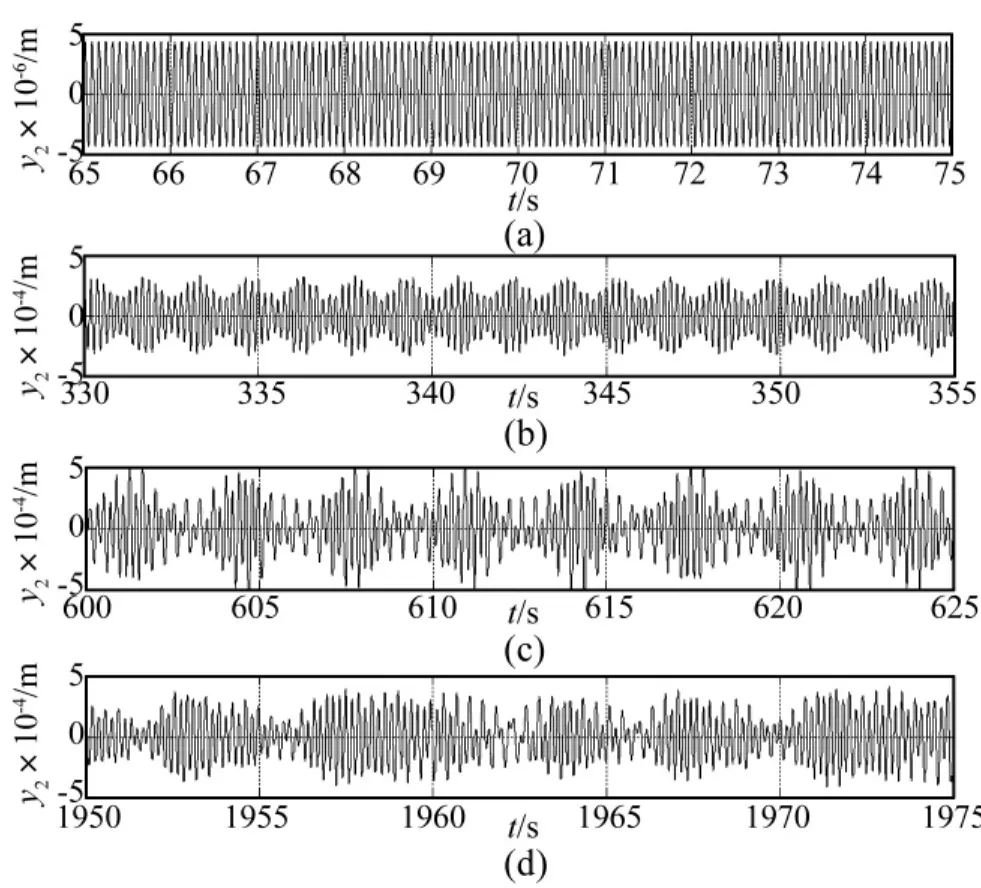
图5 混沌化过程中四个时段的系统稳态响应Fig.5 Steady state responses in four time intervals in the process of chaotification

图5给出了时间历程中四个时间段的系统稳态响应，分别为 ΔT1∶0 ～90 s，ΔT4∶270 ～360 s，ΔT7∶540 ～630 s，ΔTf∶1 890 ～1 980 s，其中 ΔTf是指系统最终状态的响应。系统无控制作用时，系统响应为周期，如图5(a)、图6(a)所示，其功率谱为线谱。ΔT4时间段内，控制器时延为0.4 s，系统稳态响应的功率谱为连续谱，最大李雅普诺夫指数(LE)为0.688 2，依此判断系统进入混沌状态，但观察响应时间历程(图5(b))，其混沌状态不甚明显。时延系统在数学意义上是无穷维动力学系统，其最大LE无法直接按照定义法计算，本文采用基于小数据量的Rosenstein方法［14］计算。ΔT7时间段内，控制器时延为1 s，系统稳态响应的功率谱为连续谱(图6(c))，最大LE为0.662 3，意味着系统响应是混沌的，且响应时间历程也可以比较明显地观察到混沌(图5(c))。时延经过不断调整，最终收敛于1.1 s，系统稳态响应如图5(d)，可以比较明显地观察到混沌，且其功率谱为连续谱，最大 LE为1.871 1。ΔT7时间段内响应虽然是混沌的，但其振动幅值明显比最终状态的幅值大，且其最大LE比最终状态的小，这说明系统最终状态的混沌特征最明显，且振动幅值较小，对于混沌隔振系统［4］是比较理想的状态。

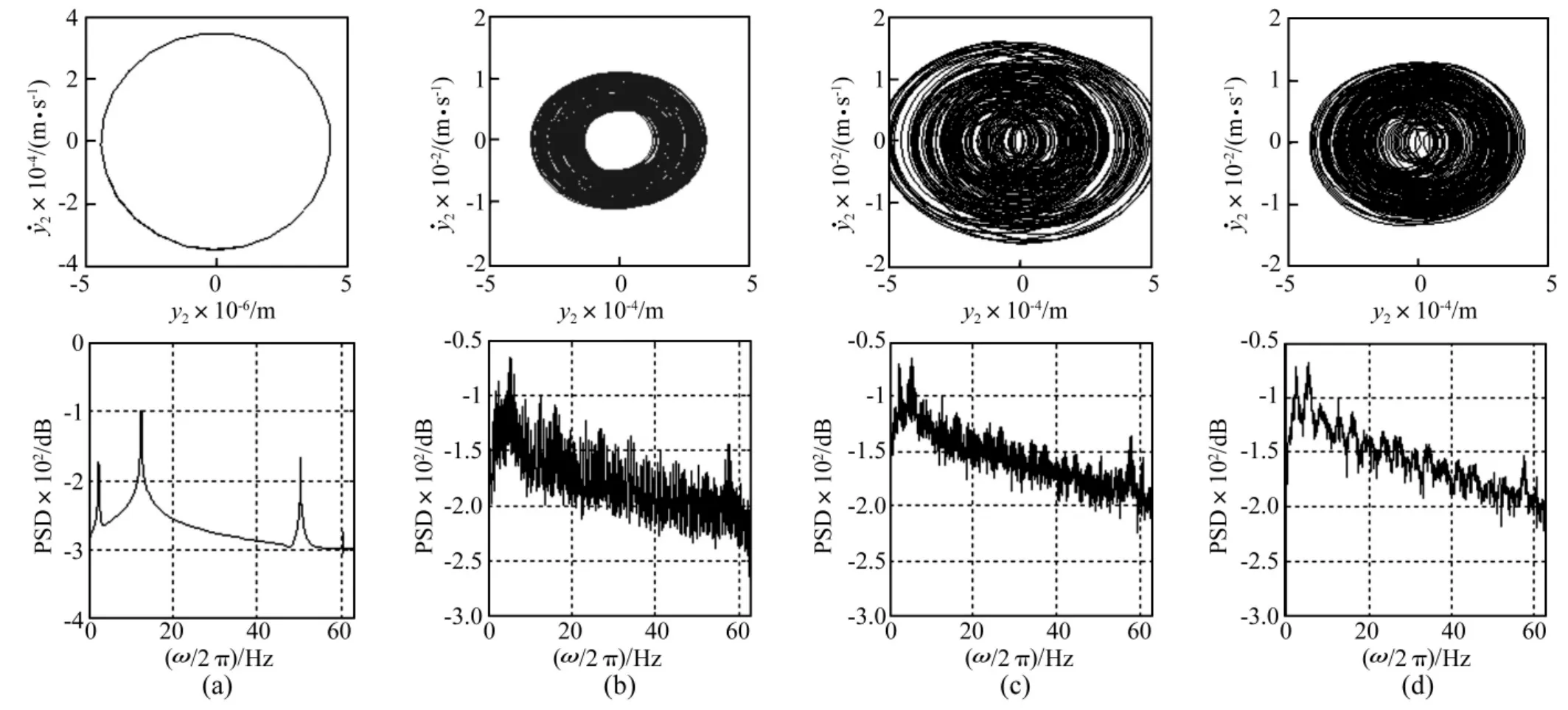
图6 与图5时程响应相对应的相图和功率谱密度(PSD)Fig.6 Phase plane and power spectrum density(PSD)corresponding to time histories in Fig.5

图7 时延(a)和性能指标(b)随性能指标计算步数的变化Fig.7 Variations of(a)time delay and(b)performance index against index evaluation count

通过上述对时程响应的分析可知，按照直接寻优算法调整时延，很容易使系统混沌化，而且随着时延逐渐趋近于最优值，系统响应混沌特性越来越明显，最终系统状态定格于混沌化性能最优的混沌状态。从图7可以观察时延和性能指标随指标计算步数的增加，也就是随着时间历程向前推进，指标值I越来越小，最终时延收敛至最优值τopt=1.1。

众所周知，混沌运动对初始条件的依赖性很强。程序开始时，及ΔT1∶0～90 s，系统初始条件为(0，0，0，0)，但随着时间推进，每个时间段ΔTk的初始条件都是继承前一个时间段ΔTk－1的末了状态，那么，对于作用相同时延的控制，性能指标I可能因初始条件不同而不同，也就是说，性能指标与时延不是完全一一对应的。然而，本文数值仿真的结果已经证实:假设性能指标与时延一一对应的前提下得到的‘最优’时延能使系统处于较好的混沌状态。

需要说明的是，对于未知参数系统，为更好地实现对系统的控制，首先应根据系统响应，对系统进行参数识别获取系统近似参数，把握系统的振动动力学特性，然后再利用本文的控制方法对系统进行混沌化。

3 结论

本文针对未知参数系统提出一种基于频谱优化和时延反馈控制的实时混沌化方法。本方法仅需系统稳态响应构造性能指标，然后依照直接寻优方法调整时延反馈控制器参数——时延，直至算法收敛，使系统混沌化。仿真结果表明:该方法能有效地实现未知参数系统的混沌化，且本方法量化系统状态，将混沌化问题转化为优化问题，跨越了界定混沌参数域的传统方法，解决了目前混沌化方法无法解决的问题。因此，本方法对于工程实际系统易于实现实时控制。针对实际系统的混沌化试验研究是我们即将开展的工作。

致 谢

感谢海军工程大学朱石坚教授提供数值仿真模型参数，以及与博士研究生杨庆超的有益讨论。

［1］陈关荣，汪小帆.动力系统的混沌化:理论、方法与应用［M］.上海:上海交通大学出版社，2006.

［2］LOU J，ZHU S，HE L，et al.Application of chaos method to line spectra reduction［J］.Journal of Sound and Vibration，2005，286(3):645－652.

［3］ YU X，ZHU S，LIU S.A new method for line spectra reduction similar to generalized synchronization of chaos［J］.Journal of Sound and Vibration，2007，306(3 － 5):835－848.

［4］ WEN G，LU Y，ZHANG Z，et al.Line spectra reduction and vibration isolation via modified projective synchronization for acoustic stealth of submarines［J］.Journal of Sound and Vibration，2009，324(3－5):954－961.

［5］ Liu S，Yu X，Zhu S.Study on the chaos anti-control technology in nonlinear vibration isolation system ［J］.Journal of Sound and Vibration，2008，310(4 － 5):855－864.

［6］张振海.基于离散混沌化的线谱控制技术研究［D］.武汉:海军工程大学，2010.

［7］Konishi K.Generating chaotic behavior in an oscillator driven by periodic forces［J］.Physics Letters A，2003，320(2 －3):200－206.

［8］Wang X F，Chen G.Chaotifying a stable LTI system by tiny feedback control［J］.IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications，2000，47(3):410－415.

［9］Wang X F，Chen G，Yu X.Anticontrol of chaos in continuous-time systems via time-delay feedback［J］.Chaos，2000，10(4):771－779.

［10］ Xu J，Chung K W.Effects of time delayed position feedback on a van der Pol-Duffing oscillator［J］.Physica D:Nonlinear Phenomena，2003，180(1－2):17－39.

［11］ Zhou J，Xu D，Li Y.Chaotifing duffing-type system with large parameter range based on optimal time-delay feedback control［C］.Proceedings of 2010 International Workshop on Chaos-Fractal Theories and Applications，Kunming，China，Oct.29 －31.2010.

［12］ Liu G R，Han X.Computational inverse techniques in nondestructive evaluation［M］. Boca Raton:CRC Press，2003.

［13］ Moon F C.Chaotic vibrations:an introduction for applied scientists and engineers［M］.New York:John Wiley ＆Sons，1987.

［14］ Rosenstein M T，Collins J J，De Luca C J.A practical method for calculating largest Lyapunov exponents from small data sets［J］.Physica D:Nonlinear Phenomena，1993，65(1－2):117－134.