挂篮模板主桁架滑行轨道梁的力学计算
2013-09-08刘旭阳
■ 刘旭阳
挂篮模板主桁架滑行轨道梁的力学计算
■ 刘旭阳
1 概述
挂篮是预应力混凝土连续梁、T形刚构和悬臂梁悬臂分段施工的一种重要设备。它是一种能够沿轨道梁整体向前移动的承重结构,通过锚固将其悬挂在已施工的前端梁上后,就可以在挂篮上进行下一节梁段的模板、钢筋、预应力管道的安设,混凝土的灌注和预应力的张拉、灌浆等作业。完成一个阶段的循环后,挂篮即可前移并固定从而进行下一节段的悬灌,如此循环至悬臂灌筑完成。
由于梁段的模板安装、钢筋绑扎、管道安装、混凝土浇筑、预加应力及管道压浆等均需挂篮上进行又系高空作业并且为梁段的承重结构,所以,挂篮设计除应保证强度安全可靠外,还应满足刚度变形小和稳定性能好;并且还应行走方便、锚固与拆装容易,安全设施完备。
2 挂篮的基本组成
目前施工中使用的挂篮结构形式有多种样式,但其基本组成有以下五部分组成,现以菱形挂篮为例说明(参见图1):
2.1主承载桁架体;见图1中的3—菱形架体结构;
2.2悬吊与锚固系统;见图1中的2—锚固装置;4—上前横梁;5—前吊带;8—后吊带;11—千斤顶等。
2.3走行系统;见图1中的1—主桁架滑行轨道梁;9—外模滑梁;及内模滑梁等。
2.4模板系统;见图1中的7—底模;10—外模板;及内模板。
2.5操作平台;见图1中的6—张拉平台等。
由于挂篮设备的特殊性,无论铁路桥涵施工规范(TB10203-2002),还是公路桥涵施工技术规范(JTJ041-2000)都对其提出了严格的力学性能要求,各生产厂家在进行挂篮及模板设计时都会对各部分进行完整的力学分析和计算。并将计算说明书提供给施工单位。施工单位为了确保挂篮设备的安全可靠还会请专门的科研机构或院校对挂篮进行第三方验算。然而,在多年的实际工作中发现不知何故,各方却都忽视了挂篮在主桁架滑行轨道梁上滑行状态下轨道梁的安全性计算和验算。
3 挂篮主桁架行走时轨道梁的力学计算方法
挂篮行走系统分别由桁架行走系统、外模行走系统及内模行走系统组成。
3.1 桁架行走系统的布置
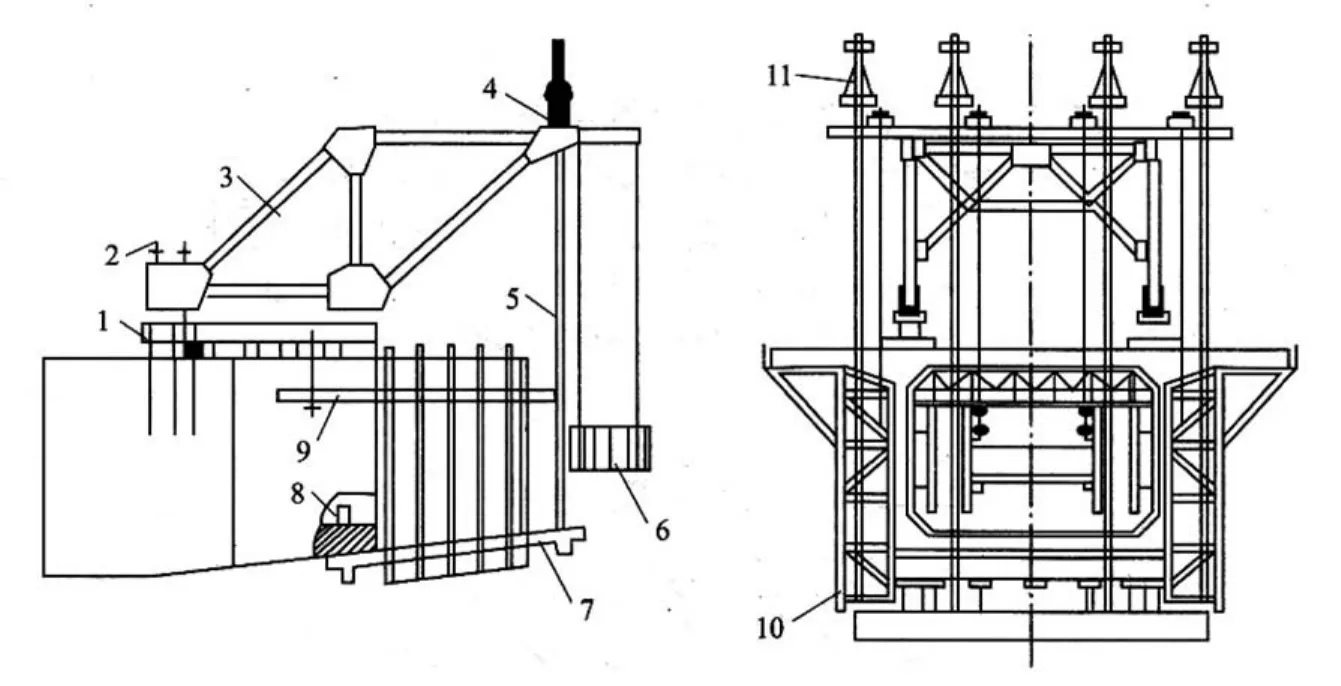
图1菱形挂篮示意图
桁架行走系统的布置为:在主桁架下的箱梁顶面铺设用钢板和型钢组焊的轨道梁,轨道梁用竖向预应力筋通过短梁固定;轨道梁顶面放置前、后支座,支座与桁架节点栓接。行走时前支座沿轨道梁滑行,后支座以反扣轮的形式沿轨道梁顶板下缘滚动,不需要加设平衡重。行走到位后,需用Ⅳ级冷拉精轧钢筋将轨道梁和桁架后节点锚固,使得后支座反扣轮不受力。轨道梁分节制造以方便倒用。
行走的具体步骤为:脱模前,用手动葫芦将底模架吊在外模走行梁上,解除底模后吊带;脱模后,底模、外模与主桁架同步行走。内模脱模后,内模架落在内滑梁上,人工用手动葫芦即可将其移动至下一梁段。前、后支座的结构示意图参见图2~4。

图2单根型钢导轨与后支座结构示意图

图3双型钢组合轨道梁与后支座结构示意图

图4双型钢组合轨道梁与前支座结构示意图
3.2 轨道梁的力学分析计算
轨道是典型的承受横向荷载的受弯构件,是典型的梁结构。因此,在力学分析中,将挂篮轨道称为“轨道梁”。依据铁路(公路)施工规范规定;要求挂篮在施工和行走时的抗倾覆稳定系数均不得小于2.0。因此,必须对轨道进行两种工作状态的承载能力计算。
3.2.1 施工状态
在施工状态下,轨道梁主要承受前支座传递来的施工荷载、挂篮自重及锚固荷载等全部荷载。因此,应按照局部承压条件下的折算应力进行计算和校核。
3.2.1.1抗弯强度的计算
按照GB50017-2003《钢结构设计规范》的规定:在考虑了截面部分发展塑性变形的情况下,在主平面内受弯的实腹构件,其抗弯强度应按下列公式计算:

当单向弯曲时,公式变为:
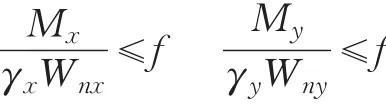
式中:
Mx、My:同一截面处绕x轴和y轴的弯矩(对于工字形截面;x轴为强轴,y轴为弱轴);
Wnx、Wny:对于x轴和y轴的净截面模量;
γx、γy:截面塑性发展系数,这里不考虑塑性发展,取其值为1.0;
f:钢材的抗弯强度设计值 (注意与厚度有关)。
3.2.1.2抗剪强度的计算
按照GB50017-2003《钢结构设计规范》的规定:在主平面内受弯的实腹构件(不考虑腹板屈曲后强度),其抗剪强度按下式计算:

式中:
V:计算截面沿腹板平面作用的剪力;
S:计算剪应力处以上毛截面对中和轴的面积矩,当计算翼缘板上的剪应力时,S取计算点以外的毛截面对中和轴的面积矩。
I:毛截面惯性矩;
tw:腹板厚度;
fv:材料的抗剪强度设计值。
3.2.1.3局部承压强度计算
按照GB50017-2003《钢结构设计规范》的规定:在集中荷载作用下,腹板计算高度上外边缘的局部承压强度应按下式计算:

式中:
F:集中荷载;
ψ:集中荷载增大系数,对于此处取1.0;
tw:腹板厚度;
f:钢材的抗弯强度设计值
lz:集中荷载在腹板计算高度边缘的假设分布长度。
在如图5(a)所示的情形下,计算公式如下:

在如图5(b)所示的情形下,计算公式如下:

式中:
a:集中荷载沿梁跨度方向的支撑长度,对钢轨上的轮压可取为50mm.;
l:自梁顶面至腹板计算高度上边缘的距离;
i:钢轨的高度,对梁顶无钢轨的梁。
3.2.1.4折算应力的计算
按照GB50017-2003《钢结构设计规范》的规定:折算应力的经验计算公式为:

式中:
σ、σc、τ为腹板高度边缘同一点上同时受到的正应力、剪应力和局部压应力,τ和σc按照3.2.1.2和3.2.1.3两条的公式计算,正应力σ应按下式计算:
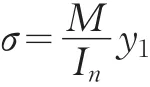
σ和 σc以拉应力为正值,压应力为负值;
In为梁的净截面惯性矩;
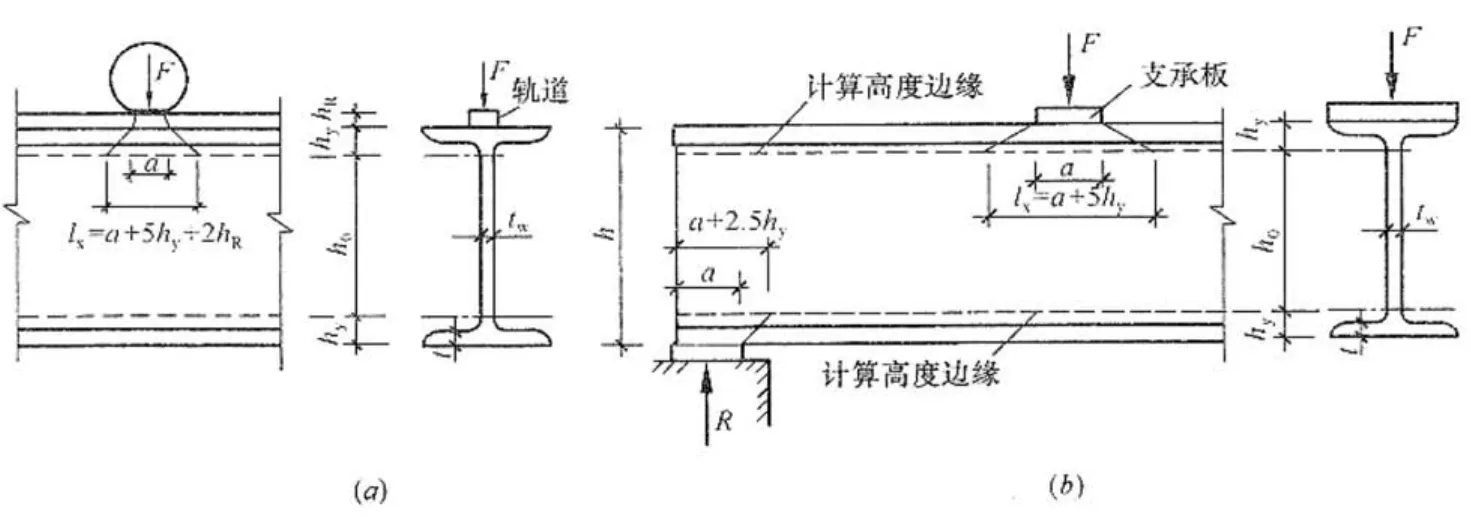
图5局部承压计算示意图
y1为所计算点至梁中和轴的距离;
β1为计算折算应力的强度增大系数;当 σ和σc异号时取1.2;当σ和σc同号或σc=0时取1.1。
至此即完成了主桁架轨道梁在施工状态下前支座处的受力计算。
3.2.2 行走状态
在行走状态下,轨道梁既承受前支座传递来的挂篮自重及后支座滚轮反力荷载(此时的荷载远小于施工状态荷载),又承受后支座滚轮的竖直向上的倾覆荷载,为了使用手册数据和叙述方便,我们将后支座旋转180度,使翼缘板受力的方向竖直向下,来进行描述和分析。
由于前支座与后支座的作用点距离远大于枕木对轨道梁的支撑间距和锚固间距,因此,可将前、后支座对轨道梁的作用视为相互独立的状态进行分析计算。而在行走状态下前支座传递的荷载远小于施工状态,所以当施工状态能够满足时,行走状态即自动得到满足。因此,行走状态的力学分析和计算的重点是后支座处轨道梁的局部应力和整体应力的复合应力计算。
如图6所示;支座移动时的荷载通过小车的轮子直接作用在轨道梁的下翼缘的内表面上。

图6轨道梁下翼缘板的局部受力分析图
基本假设:无论是普通工字钢、H型钢或焊接工字钢均假设腹板两边作用力对称;翼缘悬出部分局部变形也对称;翼缘根部与腹板连接处不发生扭转。因此,认为腹板两边的翼缘是固接于腹板,且承受集中荷载的无限长的悬臂板。
翼缘板的悬伸部分在轮压的作用下分别在轮压作用点、翼缘根部和翼缘外边缘产生局部弯曲变形和局部应力。这三个位置的纵向应力和横向应力的计算公式和系数图表如下:
翼缘根部的横向应力:

翼缘根部的纵向应力:
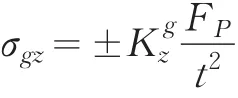
轮压作用点的横向应力:轮压作用点的纵向应力:
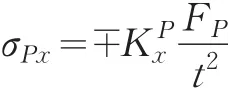
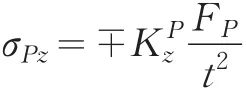
翼缘外边缘的纵向应力:

式中:
Fp:腹板一边的单轮的最大轮压设计值;
t:工字梁斜坡翼缘的平均厚度(距b|d处)或平翼缘的厚度。
公式中的正负号:表示翼缘内外表面计算的的应力符号;拉应力为正;压应力为负。 σgz应力符号与结构有关;(a)当为斜坡翼缘时,内表面为压应力;外表面为拉应力。(b)当为平翼缘时有三种情况:当ξ>0.46时,内表面为拉应力、外表面为压应力,而值不同;当ξ=0.46时,内、外表面应力为零;当ξ<0.46时,内外表面应力改变符号。
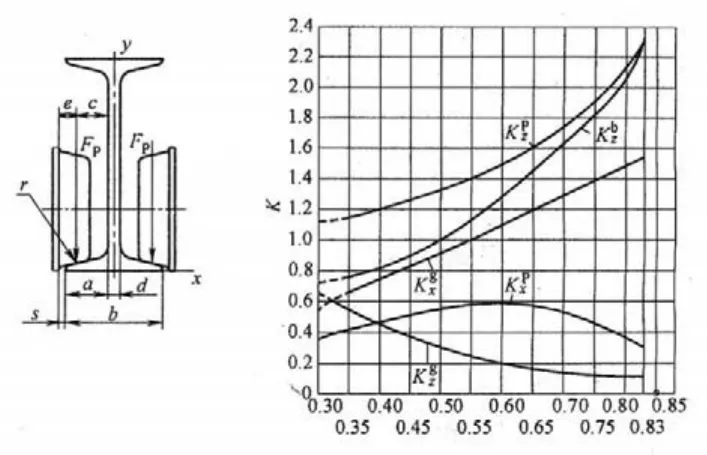
图7普通工字钢的技算系数图
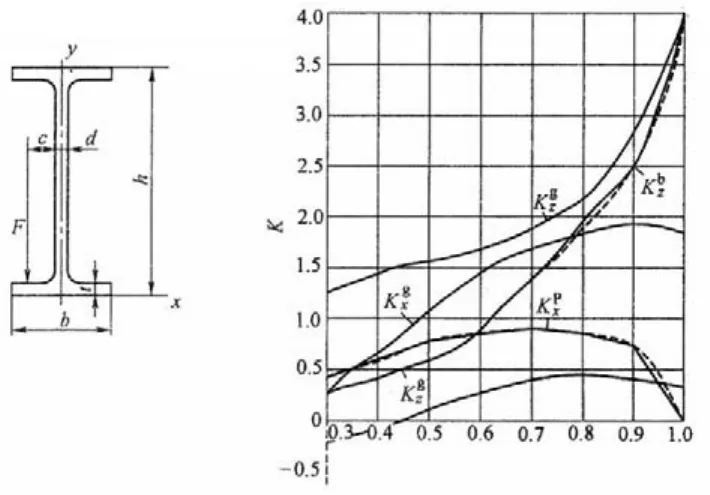
图8平翼缘H型钢的技算系数图
轨道梁在整体弯曲应力和局部弯曲应力的共同作用下,下翼缘的外表面各点会出现大的合成应力。
翼缘根部和轮压作用点的应力呈现为平面应力状态,其合成应力的计算公式分别如下:
翼缘根部的合成应力:

式中:
σ0为轨道梁整体弯曲变形产生的拉应力(下同):

轮压作用点的合成应力:

翼缘外边缘只受单向应力的作用,其合成应力为:
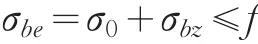
由于小车的前后轮轮距一般都超出了局部弯曲变形的影响范围,故只需计算一个轮压产生的局部弯曲应力即可,不必考虑相邻轮压的影响。
通常,国标中所提供的工字钢或H型钢翼缘的厚度均不能满足挂篮行走状态下的强度要求,为此必须对翼缘进行加厚处理方可保证挂篮的行走安全性要求,即行走时的抗倾覆稳定系数不得小于2的规定。
[1]张晓炜,智小慧.高速铁路桥梁施工技术与装备.华中科技大学出版社 2010年
[2]董军,曹平周.钢结构原理与设计.中国建筑工业出版社 2008年
[3]胡宗武,汪西应,汪春生.起重机设计与实例.机械工业出版社2009年
宁夏永治钢模板制造有限公司)
TU755.21
A
1671-3362(2013)10-0087-03
