超磁致伸缩致动器能量损耗特性分析

崔 旭 何忠波 李冬伟 李玉龙 薛光明

军械工程学院，石家庄，050003

0 引言

超磁致伸缩材料（giant magnetostrictive material，GMM）是一种新型功能材料，具有高响应速度、宽工作频域、大输出应变等优异特性，因此受到高度的关注并得到广泛应用［1］。超磁致伸缩致动器（giant magnetostrictive actuator，GMA）是以棒状GMM为核心的基本机械能输出部件，在微位移控制、精密加工、主动隔振以及流体控制等领域具有广阔的应用前景［2－4］。

但在高频驱动下的GMA中，GMM以及励磁线圈产生的大量能量损耗容易导致GMA内部温升。而GMM对温度变化也较为敏感，首先，GMM的磁致应变能力会随着温度的变化而变化；其次，数十摄氏度的温度变化下GMM的热应变几乎与磁致应变达到同一个数量级［5］。因此，超磁致伸缩器件必须具有较强的温度控制能力，而掌握GMA能量损耗特性是其温控系统设计的必要前提。

文献［6－7］在考虑涡流损耗、异常损耗以及磁滞损耗的基础上提出了改进型J－A模型，该模型能够较为准确地描述GMM等铁磁材料磁化过程。当前有关GMA能耗特性研究的文献多以GMM内部磁场分布均匀为基础进行理论分析，但动态驱动下GMM内部磁场分布并不均匀［8－9］。

本文提出了动态驱动下GMM内部平均磁场分布计算方法，并结合改进型J－A模型及线圈阻抗公式对GMA的能耗特性进行分析。将该模型计算结果与实验相比较，二者较为吻合，证明了本文方法的正确性。

1 GMA结构及工作原理

超磁致伸缩致动器结构如图1所示，线圈由漆包线绕制，线圈骨架材料为工程塑料。当励磁线圈 通 电 产 生 磁 场 后，GMM 棒（φ10mm×75mm）即可产生磁致伸缩现象。由于励磁线圈可以提供较高频率的励磁磁场，而GMM又具有分辨率高、响应快等优点，所以超磁致伸缩致动器能够快速、准确地推动负载。本文实验用致动器采用两只对合的碟片弹簧提供预压应力，以保证GMM棒产生较大的输出应变。

图1 超磁致伸缩致动器结构简图

2 能量损耗模型

2.1 GMM能量损耗

动态驱动下，GMM棒中磁场沿径向分布并不均匀。根据麦克斯韦方程，GMM棒中磁场分布的柱坐标系方程为［10］

其中，H 为磁场强度；k2＝jωμσe，ω 为励磁磁场的角频率，μ为GMM磁导率，GMM电导率σe＝1／ρ，ρ为材料的电阻率。式（1）为零阶修改贝塞尔方程，其解为一类修改贝塞尔函数I0（kr）。当线圈提供的磁场强度为H0ejωt时，直径为r0的GMM棒料内部r处磁场分布可表示为

GMM电导率较大，当驱动频率ω也较大时，｜kr｜→ ∞，由贝塞尔函数渐近公式［11］：

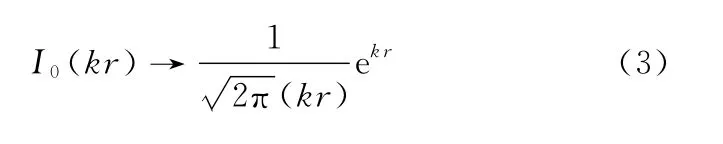
有

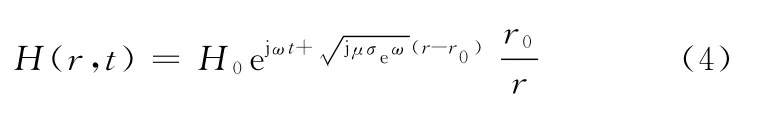
由式（4）可知，GMM棒中磁场强度径向分布不均，且磁场强度大小随着驱动频率的变化而变化。GMM棒径向截面平均磁场强度可表示为

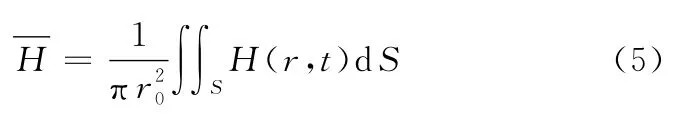
式中，S为GMM棒横截面积。

在J－A模型的基础上，文献［7］在假设磁场分布均匀的前提下推导了用于描述GMM棒动态磁滞特性的J－A模型［6-7］：

式中，ke为不可逆损耗系数；G为常数；μ0为真空磁导率；d为GMM棒直径；β为形状因子；V0为畴壁运动参数；c为可逆系数。

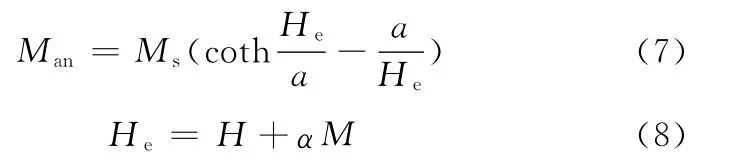
式中，a为形状系数；α为畴壁相互作用系数。

磁化强度M可表示为

2.2 线圈能量损耗

励磁线圈及线圈骨架的结构如图2所示，线圈骨架参数见表2，励磁线圈能耗是GMM器件发热的重要来源之一。

表1 GMM能耗模型中的参数

图2 线圈尺寸图

表2 线圈参数

假设线圈内部磁场强度分布均匀，线圈通电电流为I，线圈内部磁场强度计算公式［10］为

线圈中通入交变电流后的阻抗表达式为

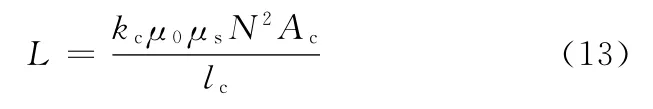
其中，GMM相对磁导率μs＝10，尺寸系数kc＝0.87，线圈的有效截面面积Ac＝1429mm2，联立式（11）～式（13）即可计算不同频率驱动下线圈的阻抗。

线圈感抗Lct可表示为

线圈电感的经验计算公式［13］为

当线圈中通入交变电流时，线圈的能耗为

综合考虑GMM棒以及线圈的损耗就能获得超磁致伸缩致动器的损耗特性。

3 GMA能量损耗分析

3.1 GMA频率相关的能耗特性

当考虑材料内部磁强分布状况时，需先利用式（5）计算材料内部平均磁场强度，然后将平均磁场强度代入式（6）求解。当要求致动器线圈产生大小为 H＝40sin（2πf t）的励磁磁场时，由式（10）计算可得所需要的励磁电流为I＝2sin（2πf t）。当驱动频率f 分别为50Hz、100Hz、500Hz的B－滞回曲线如图3所示，随着频率的增大，每周期能耗逐渐增大。由式（11）～式（14）求解所得该励磁电流下线圈功耗－频率特性如图4所示，线圈单位时间能量损耗随着频率增大而增大。

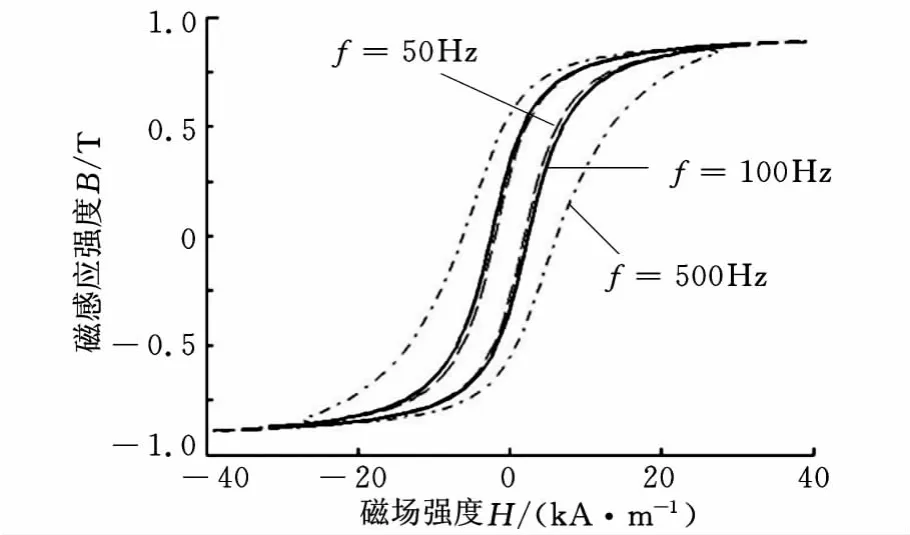
图3 考虑材料内部磁场分布时B－H滞回环

图4 线圈的频率－能耗特性

首先由式（1）～式（9）计算B－H滞回环，并计算滞回环面积，然后将面积乘以GMM棒体积以及对应的驱动频率，得到单位时间内GMM棒能量损耗，再与单位时间内线圈能量损耗值叠加即可解得GMA能耗P。不同的励磁电流驱动下单位时间总功耗随着频率变化曲线如图5所示，GMA能量损耗随着驱动电流以及驱动频率的增大而增大。低频驱动（0～50Hz）下的GMA的能耗特性受频率影响较小；高频驱动（50Hz以上）下的GMA能耗随着频率的增大而急剧增大，驱动电流为0.5A时，500Hz下能耗可达100Hz下能耗的4倍。随着频率的增大，GMM棒能量损耗逐渐增大，驱动电流为2.0A、频率为500Hz时GMM能耗达40W，而频率为100Hz时GMM能耗却只有16W。并且随着频率的增大，GMM棒能耗占GMA总能耗比例增加，驱动条件为2.0A、500Hz时GMM 能耗比例达总能耗的30%，而频率为100Hz时却只有7%。

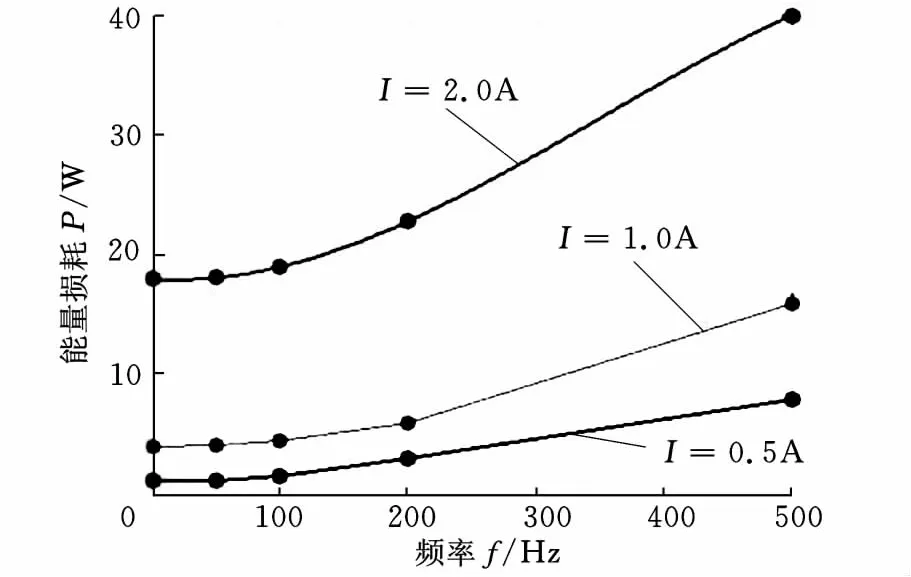
图5 不同电流驱动下GMA总能耗

3.2 GMA频率相关的温升特性

在高频驱动下，虽然GMM棒能耗小于线圈能耗，但因线圈体积较大且散热较好，故热平衡后的线圈温度相对较低；而GMM棒体积相对较小，大量的能耗使得GMM棒温度急剧上升，为了控制GMM的剧烈温升，在GMM棒与线圈骨架间的同心空腔通入流动的冷却油，冷却油油温控制在21℃。

假设GMM棒内部发热均匀，由GMM能耗除以GMM棒体积即可得到单位体积GMM的产能率。可计算得驱动电流为2.0A、驱动频率为500Hz时＝2MW／m3，冷却到稳态条件下的GMM棒表面温度为［14］

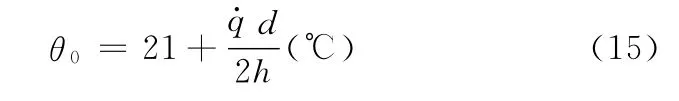
假设冷却油层流流动，对流条件h计算公式为

由文献［14］查得，充分发展的层流同心腔内壁努塞尔数Nu≈5，冷却油热导率λ0＝0.386W／（m·K）。空心管当量直径Dh＝φf－d＝3.6mm，可得对流条件h＝526W／（m2·K）。

经计算得θ0＝40℃。 同理，驱动频率为500Hz、驱动电流分别为1.0A和0.5A时，与上述条件相同的油冷条件下，理论的稳态冷却温度分别为31.9℃和23.7℃。GMM棒表面温度可由实验实测，与理论计算进项对比。

4 GMA能耗实验

为了测试GMA的工作特性，设计了图6所示的实验系统，该实验系统可以实时测量GMA动态驱动下GMM棒表面磁场强度、表面温度、磁感应强度以及磁致伸缩应变等参数，其中温度测量传感器为赛亿凌科技STT－FB3温度芯片。选择驱动电流分别为0.5A、1.0A、2.0A，驱动频率为500Hz，在0～180s内进行无冷却驱动，180s后进行强制油冷条件下驱动。

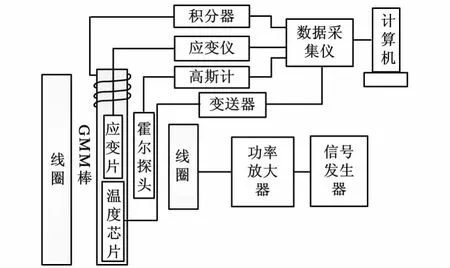
图6 GMA动态实验系统

实验结果如图7所示，以2.0A驱动电流为例，没有通入冷却油的条件下GMM表面温度在180s时可达63℃，而通入冷却油液的条件下GMM达到热平衡后的表面温度为37.5℃，冷却效果较为明显。同时0.5A和1.0A驱动下油冷热平衡后的温度分别为30.6℃和24.1℃，油冷条件下3组实验结果与计算结果较为接近，证明了理论推导的正确性。GMM在0～90℃的范围内磁致伸缩率较大且变化不明显［10］，该冷却系统能将温度控制在40℃左右，故可以满足冷却要求。

图7 GMM表面温度变化

5 结论

（1）本文推导了动态驱动下GMM内部磁场分布计算公式，结合动态J－A模型，提出了考虑磁场分布时的GMM能耗计算方法；在此基础上分析了GMM棒、线圈以及GMA频率相关的能耗特性；利用导热方程计算了油冷状态下的GMM表面温度，计算结果与实验结果较为接近。

（2）低频驱动阶段，引起GMA能耗的主要因素为线圈的阻抗；随着驱动频率的提高，GMM棒所产生的能耗逐渐增大，GMM棒能耗占GMA总能耗比例增加。虽然GMM棒能耗量不及线圈能耗，但由于GMM棒体积较小，容易导致剧烈的温升。

（3）为了控制GMM棒温度的剧烈变化，致动器采用油冷的方式对GMM棒进行冷却，油冷系统能将GMM棒表面温度控制在较低的范围内（2.0A、500Hz驱动条件下GMM表面温度为37.5℃），所以GMA的冷却系统性能满足冷却要求。同时冷却系统实验也验证了所提出的能耗计算模型的正确性。

（4）GMA能耗特性的分析对GMA设计及控制具有重要的意义：首先，GMA设计时应充分考虑高频驱动下因GMM内部磁场分布不均而导致的输出能力有所下降的现象，其次，GMA冷却系统的设计应在充分了解线圈及GMM能耗特性的基础上进行，最后，根据得到的M－滞环设计对应的逆模型可以对GMA进行逆补偿控制。

［1］Karunanidhi S，Singaperumal M.Design Analysis and Simulation of Magnetostrictive Actuator and Its Application to High Dynamic Servo Valve［J］.Sensors and Actuators A：Physical，2010，157：185－197.

［2］石延平，刘成文，张永忠.一种大流量高速开关阀的研究与设计［J］.机械工程学报，2004，40（4）：195－198.Shi Yanping，Liu Chengwen，Zhang Yongzhong.Design and Study of a New Kind of Larger Flow Rate High－speed on－off Valve［J］.Journal of Mechanical Engineering，2004，40（4）：195－198.

［3］Moona Seok－Jun，Limb Chae－ Wook，Kima Byung－ Hyun.Structural Vibration Control U－sing Linear Magnetostrictive Actuators［J］.Journal of Sound and Vibration，2007（302）：875－891.

［4］李东，袁惠群.超磁致伸缩换能器耦合磁弹性模型与振动特性分析［J］.固体力学学报，2011，32（4）：365－371.Li Dong，Yuan Huiqun.Analysis on Coupling Magneto－elastic Characteristic of a Giant Magnetostrictive Transducter［J］.Chinese Journal of Solid Mechanice，2011，32（4）：365－371.

［5］Dapino M J.Nonlinear and Hysteretic Magnetomechanical Model for Magnetostrictive Transducers［D］.Ames：Lowa State University，1999.

［6］Jiles D C.Modelling the Effects of Eddy Current Losses on Frequency Dependent Hysteresis in Electrially Conducting Media［J］.IEEE Trans.Magn.，1994，30（6）：4326－4328.

［7］孙乐.超磁致伸缩材料的本构理论［D］.兰州：兰州大学，2007.

［8］孙华刚，袁惠群.超磁致伸缩材料内部磁场与涡流损耗理论分析［J］.东北大学学报（自然科学版），2008，29（3）：371－374.Sun Huagang，Yuan Huiqun.Theoretical Analysis of Magnetic Field and Eddy Current Loss Within Giant Magnetostrictive Material［J］.Journal of Northeastern U－niversity（Natural Science），2008，29（3）：371－374.

［9］Mauro Zucca，Paolo E.Roccato，Oriano Bottauscio，et al.Analysis of Losses in a Magnetostrictive Device under Dynamic Supply Conditions［J］.IEEE Trans.Magn.，2010，46（2）：183－186.

［10］贾振元，郭东明.超磁致伸缩材料微位移执行器原理与应用［M］.北京：科学出版社，2008.

［11］汪建新，高耀东，任冲珝.磁致伸缩材料在高频驱动时内部磁场分布及其对磁致伸缩性能的影响［J］.机械传动，2007，31（6）：21－23.Wang Jianxin，Gao Yaodong，Ren Chongchong.The Distribution of Internal Magnetic Field in Cylindrical Shaped Terfenol－D Material and the Effect of the Field on Magnetostrictive Property of the Material［J］.Journal of Mechanical Transmission，2007，31（6）：21－23.

［12］Jiles D.Challenges in Incorporating Nonlinear Hysteretic Behaviour into Modelling of Magnetic Materials［R］.London：the Institution of Engineering and Technology Electromagnetic Professional Network，2006.

［13］Raghavendra A.High Frequency High Amplitude Magnetic Field Driving System for Magnetostrictive Actuators［D］.College Park：University of Maryland，2009.

［14］Incropera F P，Dewitt D P，Bergman T L，et al.Fundamentals of Heat and Mass Transfer［M］.Hoboken：John Wiely ＆ Sons，Inc.2007.