基于Kriging模型的发动机罩多目标优化设计

陈立娜 张维刚

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

汽车安全是汽车产业的三大主题之一，行人保护也日渐成为人们关注的热点问题。据有关资料统计，在与行人直接相关的交通事故中17.3%的头部伤害与发动机罩相关，因此，合理设计发动机罩的结构与材料，可以大大降低行人在与车辆发生碰撞时所受的伤害。

在发动机罩的设计过程中，研究者要综合考虑安全性、刚度及轻量化等要求，而这些要求往往是相互冲突的，因此发动机罩的优化设计过程是一个多目标优化问题。多目标优化即是在各个目标之间反复考量，然后找到一个最优折中方案。考虑到碰撞过程中的非线性及计算时间长的问题，在处理多目标问题时引入近似模型，在保证一定精度的情况下，构造一个计算量小、计算结果与实际仿真结果相似的数学模型代替实际仿真程序，并在优化迭代过程中不断更新模型、提高精度，使多目标优化更快更有效地达到收敛。

作为一种常用的近似模型，Kriging［1］模型起源于地理空间统计学，是一种估计方差最小的无偏估计模型，具有局部估计特点，可以较好地预估未知函数点处函数值的分布情况，进而可以替代原有的目标函数分析模型，在汽车零部件优化设计上具有很大的应用价值。

1 问题描述

1.1 头部冲击仿真模拟

取某轿车的发动机罩为研究对象，主要包括内板、外板、加强板和铰链，如图1a所示。按照欧洲EEVC／WG17［2］标准建立成人头部冲击器，由后盖（back plate）、球体（sphere）、头皮（skin）及包裹在外面的空材料壳单元（null shell）组成，如图1b所示。整个头锤质量为4.8kg，头皮厚度为14mm。

参照EEVC标准，建立的头部撞击发动机罩有限元模型如图2所示。头部冲击器与发动机罩接触时的速度为40km／h，撞击角度为65°，撞击点选择包络线范围（WAD：1500～2100mm）内靠近铰链处位置。

图1 仿真模型的组成

图2 头部撞击发动机罩有限元模型

以头部伤害指标 HIC（head injury criteria）值作为头部损伤的评价指标：

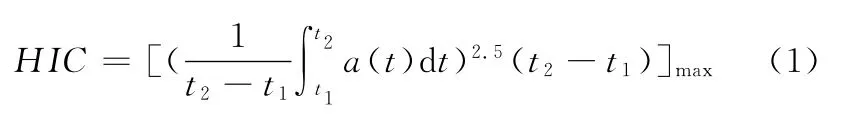
式中，a为头部质心合成加速度；t为HIC值达到最大时的时间间隔，在行人事故中计算值最大为15ms。

在LS－DYNA中进行模拟仿真，得到最大加速度值为119.5m／s2，计算所得头部损伤值（HIC）为1099.51，大于法规规定的1000的安全限值。因此，该发动机罩系统不能满足法规要求，而且在CNCAP中得分为0，需要进行改进设计。

1.2 灵敏度分析

为确定发动机罩各部件对头部损伤的影响程度，对其进行灵敏度分析。灵敏度分析是指对系统性能因设计变量的变化表现出来的敏感程度的分析，通常用导数信息来表示。在基于近似模型的优化过程中，灵敏度是近似模型相对于设计变量的导数，这些导数信息反映了设计变量的改变对目标函数或约束函数的影响。

本文以发动机罩内板 （t1）、外板（t2）、加强板（t3）和铰链（t4）的厚度作为初始参量，运用HIC值对其进行评价，采用最优拉丁方法试验选择8组样本点，构造的一阶响应面模型为

根据式（2），通过响应面系数大小比较可以发现，在各参量中，发动机罩内板对HIC值影响最大，基于此，下面将对发动机罩内板进行结构及材料改进研究，使发动机罩在满足约束条件下达到性能最优。

2 发动机罩内板改进设计

2.1 结构改进

利用拓扑优化方法在发动机罩内板上开孔挖槽改变原结构的材料布置以降低发动机罩刚度。拓扑优化即是在给定的设计区域内寻求最优材料分布。采用变密度法来定义材料的流动规律，最常用的插值模型为固体各向同性惩罚材料插值模型 （solid isotropic material with penalization，SIMP），它假设设计材料的宏观弹性常量与其密度是非线性关系，采用惩罚因子抑制介于0～1之间的单元，寻找具有某种度量的结构材料最佳分布形式。

本文采用基于带权重的折中规划法［3］，将多工况载荷对应的多目标函数转化为单目标函数优化问题。依据SIMP密度函数插值模型，在OPTISTRUCT中建立弯曲和扭转两种工况下发动机罩的拓扑优化数学模型，其表达式为

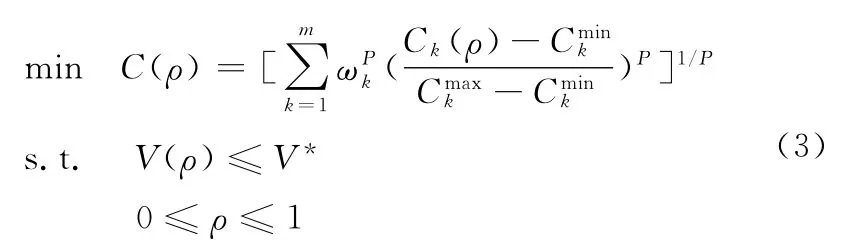
式中，ρ为单元相对密度；V、V＊分别为罩板材料总体积和给定的材料体积上限；m 为载荷工况总数；Ck（ρ）为第k个工况的柔度目标函数分别为第k个工况柔度目标函数的最大值和最小值；P为惩罚因子，P＝3，用以实现对材料中间密度的惩罚。

以弯曲和扭转工况下发动机罩的加权应变能最小化为优化设计目标，设定体积分数上限值为0.45，施加对称约束得到的拓扑优化前后的发动机罩内板几何模型如图3所示。

图3 拓扑优化结果前后对比图

2.2 模型验证

将初始模型中的发动机罩内板替换为改进后的内板，在LS－DYNA中进行数值仿真分析。改进前后头部质心加速度曲线及碰撞力曲线对比如图4所示。

由图4可知，头部质心加速度曲线及碰撞力曲线在内板改进后的峰值加速度及峰值碰撞力分别下降了14.8%和16.79%，且曲线波形图基本一致，由于外板的惯性质量产生了第一个峰值，而后与内板接触产生了第二个峰值，因此，改进后的模型是合理的，可以利用它进行下一步的多目标优化设计研究。

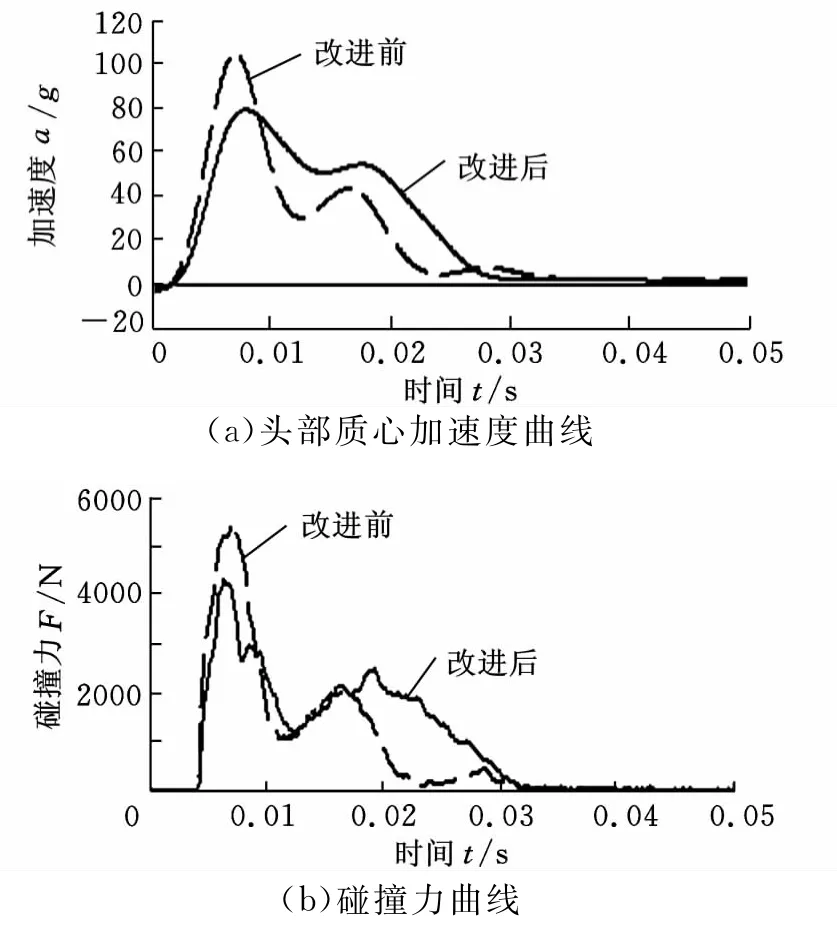
图4 改进前后曲线对比

3 基于Kriging模型的多目标优化设计

3.1 样本点选取

以发动机罩内板、外板、加强板及铰链的厚度为设计变量t1、t2、t3、t4，初始值分别为0.8mm、0.7mm、0.75mm、2.0mm，根据工程上板料厚度规定选取各变量取值范围如下［4－5］：t1，t2，t3∈［0.5，2.0］mm，t4∈［1.5，3.0］mm。利用最优拉丁方法在整个设计空间中进行20次全局采样，然后通过有限元计算程序LS－DYNA及OPTISTRUCT进行仿真计算得到质量、HIC值及模态值。

3.2 Kriging近似模型

3.2.1 Kriging模型理论

Kriging模型假定的系统响应值与自变量之间的关系为

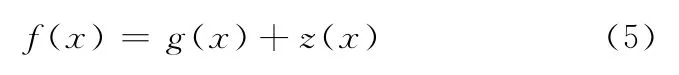
式中，f（x）为关心的未知函数；g（x）为以x为自变量的多项式函数，称为确定性漂移；z（x）为非零的随机过程，称为涨落。

z（x）非零过程涨落统计特征表达式为

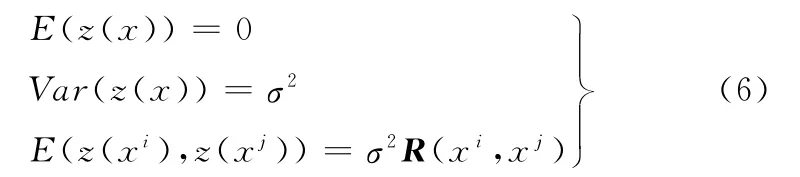
式中，σ2为方差；R（xi，xj）为关于样本中两个任意样本点xi、xj的相关函数；R为ns×ns维对角线为1的对称正定矩阵，常用高斯函数作为核函数。

相比于其他传统的插值技术，Kriging模型有两方面的优点：第一，Kriging模型以已知信息的动态构造为基础，即只使用估计点附近的某些信息；第二，Kriging模型同时具有局部和全局的统计特性，使得其可以分析已知信息的趋势和动态。

3.2.2 Kriging模型的建立

由Kriging近似模型理论可知，一旦样本点（xi，yi）确定，无约束非线性优化器便被激活来寻求最大似然函数值θi。首先随机确定一组θi值作为初始输入，然后求出θi相关矩阵R、，进而可以求出R和2，并得出一个最大似然值，该值被返回优化循环来判断是否取得最大值，当取得最大值时，循环终止并记录响应的θ值。由此可建立关于头部损伤值、质量及模态的Kriging近似模型fH、fma、fmo。通过求解器求得的似然函数最大值（MLE）和相关系数θ分别如表2、表3所示。

表2 Kriging模型最大似然函数值

表3 Kriging模型相关系数值

为检验近似模型的拟合精度，在设计空间任意选取设计方案外的3组样本点进行仿真模型与近似模型的对比，拟合情况如表4所示。

表4 近似模型拟合误差

由表3可见，构建的Kriging模型对质量、HIC及模态的拟合误差都控制在1.0%以内，表明建立的近似模型可以高精度地拟合设计变量与响应之间的关系，可以用于进行优化设计。

3.3 多目标优化

确定优化目标为：

（1）头部损伤值HIC反应了行人头部在碰撞过程中的损伤程度，要求越小越好［6］，根据欧洲NCAP规定，要达到四星标准，HIC值应小于650。

（2）考虑到车身轻量化对节能环保的重要意义，质量要求越小越好。

（3）模态分析的主要目的是避免结构模态与激励频率耦合时产生过大的车内噪声，汽车行驶中因车轮不平衡引起的激励频率一般低于11Hz，而怠速为600r／min的四缸发动机的爆发频率为20Hz，因此，发动机罩的固有频率应尽量避开这些激励所产生的频率。

基于以上分析，建立的发动机罩多目标优化模型为

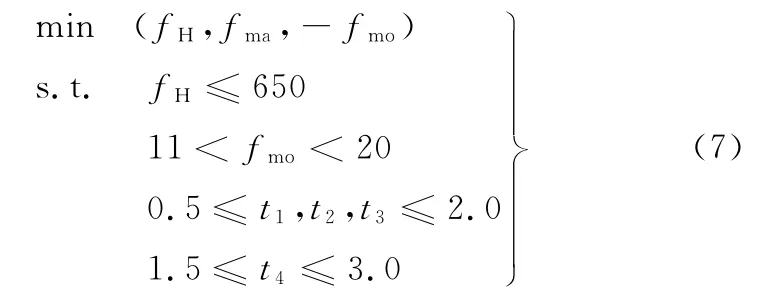
3.4 优化求解

传统的多目标优化方法如加权组合法、目标规划法等都是通过某种数学变换将多目标转化为单目标进行求解，这种方法在工程应用中往往受设计人员主观因素的影响，很难取得最优解。Deb等［7］提出的NSGA－Ⅱ多目标遗传算法，是目前公认的求解多目标问题最有效的优化算法之一。Zitzler等［8］对 MOGA（多目标遗传算法）、NSGA（非劣分层遗传算法）、NPGA（小组决胜遗传算法）进行了系统的定量实验比较，发现NSGA算法的性能是最优越的［9］。

本文利用NSGA－Ⅱ算法求解该多目标优化模型，选定的个体总数为30，经过100次遗传算法迭代得到多目标Pareto最优解集。

Pareto解集无论对于设计变量，还是目标值，都为设计人员提供了很大的设计空间，设计者可以根据对目标的期望来选取合适的设计变量。

3.5 优化结果分析

考虑到行人安全在三个目标中影响最大，选定内板厚度为0.7mm，外板厚度为0.75mm，加强板厚度为0.8mm，铰链厚度为2.5mm，采用数值分析的方法进行仿真计算［10－11］。

改进前的初始结构质量为20.63kg，改进后的最优结构质量为18.99kg，减少了7.95%；改进前的结构模态为11.81Hz，改进后的结构模态为13.07Hz，提高了10.67%，使发动机罩的防振性能得以优化；初始结构在碰撞过程中的头部损伤值为1099.51，改进后的头部损伤值为603.25，下降了45.13%，使其性能达到欧洲EEVC的四星标准，对碰撞过程中的行人头部起到了更好的保护作用。

上述分析结果表明，发动机罩内板经结构拓扑优化改进后，不仅其系统安全性和防振性能得到提高，而且因其结构轻量化更加节能环保。

4 结论

基于近似模型的灵敏度分析，针对发动机罩内板的结构特点，采用建立的Kriging近似模型并结合NSGA－Ⅱ多目标进化算法对改进后的模型进行的优化设计。优化仿真结果表明，改进后的发动机罩HIC值下降了45.13%，能够更好地提高轿车的行人保护性能，同时，质量减轻7.95%、模态值提高了10.67%，兼顾了安全性、防振及轻量化三项指标，为汽车发动机罩的研究设计提供了理论依据。

［1］Simpson T W.Kriging Models for Global Approximation in Simulation－Based Multidisciplinary Design Optimization［J］.AIAA Journal，2001，12（39）：2233－2241.

［2］European Enhanced Vehicle－Safety Committee.Improved Test Methods to Evaluate Pedestrian Protection Afforded by Passenger Cars［R］.Brussels：EEVC Working Group 17Report，2002.

［3］范文杰，范子杰，苏瑞意.汽车车架结构多目标拓扑优化方法研究［J］.中国机械工程，2008，19（12）：1505－1508.Fan Wenjie，Fan Zijie，Su Ruiyi.Multi－objective Topology Optimization of Automobile Frame Structure［J］.China Mechanical Engineering，2008，19（12）：1505－1508.

［4］廖君.车用铝合金轻量化材料［J］.汽车工艺与材料，2008（2）：8－10.Liao Jun.Vehicle Aluminum Lightweight Materials［J］.Automobile Technology ＆ Material，2008（2）：8－10.

［5］冯银成.6061铝合金热变形及时效过程中的组织力学行为研究［D］.长沙：湖南大学，2010.

［6］Koki Ikeda，Hideki Ishitobi.Development of Aluminum Hood Structure for Pedestrian Protection［J］.AE Paper，2003（1）：537－542.

［7］Deb K，Pratap A，Agarwal S，et al.A Fast and Elitist Multi－objective Genetic Algorithm：NSGA－Ⅱ［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［8］Zitzler E，Thiele L.Multi－objective Optimization Using Evolutionary Algorithms－a Comparative Case Study［J］.Parallel Problem Solving from Nature－PPSNV，1998，4（3）：292－301.

［9］王晓鹏.多目标优化设计中的Pareto遗传算法［J］.系统工程与电子技术，2003，25（12）：1558－1561.Wang Xiaopeng.Pareto Genetic Algorithm for Multi－objective Optimization Design［J］.System Engineering and Electronics，2003，25（12）：1558－1561.

［10］李莉，杨济匡.汽车与行人碰撞的动力学响应仿真研究［J］.计算机仿真，2003，20（7）：49－51.Li Li，Yang Jikuang.Stimulation Study on Dynamic Response of Pedestrian in Vehicle Front Impact［J］.Computer Simulation，2003，20（7）：49－51.

［11］高云凯，孙芳，余海燕.基于Kriging模型的车身耐撞性优化设计［J］.汽车工程，2010，32（1）：17－21.Gao Yunkai，Sun Fang，Yu Haiyan.Crashworthiness Optimization of Car Body Based on Kriging Surrogate Model［J］.Automotive Engineering，2010，32（1）：17－21.