基于信号共振稀疏分解的转子早期碰摩故障诊断方法

陈向民 于德介 罗洁思

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

近年来，旋转机械不断向着柔性化、高速化的方向发展，为了提高机组效率，转子与定子之间的间隙越来越小。当转子的振动幅值大于转子与定子之间的间隙时，必然会发生动定件碰摩。转子碰摩轻则引起机械异常振动、磨损，重则会导致断轴等恶性事故，造成巨大的经济损失。因此，转子动定件早期碰摩故障诊断技术研究具有重要意义。

当转子系统中出现动静碰摩故障时，由于转子与定子的周期性碰撞，故障信号中常常伴有周期性瞬态冲击。但当出现早期碰摩时，冲击脉冲微弱，淹没在转子自身强背景噪声环境中，不易察觉。由于瞬态冲击信号成分包含了转子早期碰摩故障的重要信息，因此，如何从强背景噪声环境中提取振动信号中的瞬态冲击成分是早期转子碰摩故障诊断的关键。

近年来，许多学者致力于转子碰摩故障诊断研究，取得了较多的研究成果。孙云岭等［1］提出利用共振解调法提取转子早期碰摩中的故障特征，该方法首先利用IFFT方法进行定子固有振动信号的分离，再进行希尔伯特变换，得到包络信号，通过对包络信号进行谱分析进行故障诊断，但需要先验知识来确定滤波的中心频率和带宽。小波具有多尺度特性和“数学显微”特性，也已成功用于转子早期碰摩故障特征的提取。李小彭等［2］利用小波时频等高图来诊断质量慢变转子系统碰摩故障。彭志科等［3］利用小波尺度谱和相位谱研究了转子碰摩故障诊断。宋友等［4］利用小波变换与多分辨分析理论，对振动信号进行多尺度分解，通过分析细节信号的能量分布研究振动信号中的碰摩特征。但小波变换缺乏自适应性，且小波基的选择难以确定，影响了其进一步应用。EMD方法为一种自适应信号处理方法［5］，已成功应用于转子碰摩的特征提取。Cheng等［6］用EMD方法对转子振动信号进行分解，实现碰摩信号、背景信号和噪声信号的分离，从而提取转子系统局部碰摩振动信号的故障特征。但EMD本质上为一正交带通滤波器组［7－8］，当持续振荡的周期信号与瞬态冲击信号频带相互重叠时，无法实现周期振动信号与瞬态冲击的有效分离，且EMD在理论上存在过包络、欠包络、模态混淆等问题，有待进一步研究。

Selesnick［9］最近提出了信号共振稀疏分解方法，与传统的基于频带划分的信号分解方法不同，该方法根据瞬态冲击信号与持续振荡周期信号品质因子（定义为中心频率与频率带宽的比值，用Q表示）的不同，将一个复杂信号分解成由持续振荡成分组成的高共振分量和由瞬态冲击成分组成的低共振分量。瞬态冲击信号为宽带信号，具有低的品质因子；持续振荡周期信号为窄带信号，具有高的品质因子，因而，根据品质因子的差异，可实现瞬态冲击信号与持续振荡周期信号的有效分离。信号共振稀疏分解方法首先根据待分析信号选择两种高低不同的品质因子，通过品质因子可调小波变换分别建立高共振分量与低共振分量的稀疏表示形式，再利用形态学分析方法建立稀疏分解目标函数，最后通过分裂增广拉格朗日收缩算法优化求解，得到信号的高共振分量和低共振分量。

本文将信号共振稀疏分解方法引入转子早期碰摩故障诊断，提出了基于信号共振稀疏分解的转子早期碰摩故障诊断方法。当转子系统发生早期碰摩故障时，重要的故障信息往往包含在瞬态冲击信号中。信号共振稀疏分解方法根据背景噪声与瞬态冲击品质因子的不同，将信号分解成包含背景噪声的高共振成分和包含冲击成分的低共振成分，通过分析低共振成分中的瞬态冲击成分进行故障诊断。算法仿真和应用实例验证了本文方法提取转子早期碰摩冲击信号的有效性。

1 信号共振稀疏分解方法

1.1 信号的共振属性

信号的共振属性用品质因子Q越大，信号的频率聚集性越好，具有越高的共振属性；反之，信号的时间聚集性越好，具有越低的共振属性。图1表示了信号共振属性的概念。图1a、图1c为信号时域波形图（用采样点数N间接表示时间），所示的信号为单周期脉冲信号，品质因子Q较小，定义为低共振信号；图1b、图1d为对应的幅值谱图，所示的信号为持续多个周期的脉冲信号，品质因子Q较大，定义为高共振信号。图1a与图1c所示的信号之间，以及图1b与图1d所示的信号之间可通过时间尺度的变化互相转化，时间尺度的变化会引起脉冲信号频率发生变化，但对信号的共振属性没有影响，即具有相同的品质因子。所以高低共振信号都可能同时包含了低频信号和高频信号。高共振信号可通过具有高Q的基函数来实现稀疏表示，而低共振信号则可通过具有低Q的基函数来实现稀疏表示。

图1 不同品质因子信号的时域波形及频谱

传统的线性滤波方法按频带划分对信号进行分解，但当信号中多个分量的中心频率相近且频带相互重叠时，如图1a与图1b、图1c与图1d所示信号的中心频率重叠在一起，此时线性滤波方法就会失效，而信号共振稀疏分解方法从信号共振属性角度出发，综合考虑了信号中心频率与频率带宽因素，能有效分离中心频率相近且中心频率带相互重叠但具有不同品质因子的信号分量。

1.2 品质因子可调小波变换

二进制小波变换作为一种恒Q变换（其Q值由所选基函数确定），在对分段光滑信号的稀疏表示中显示了其有效性，但由于其品质因子相对较低，频率分辨率不高，因而在对频率分辨率要求较高的信号分析中，二进制小波不适用［10］。有理膨胀小波［10-11］本质上为一种过完备的二进制小波变换，相对于二进制小波具有更高的品质因子和更高的频率分辨率。品质因子可调小波变换［12］与有理膨胀小波变换类似，具有完全离散、完美重构、适度完备、依赖于两通道滤波器组并能利用离散傅里叶变换计算等特点。但相对于有理膨胀小波变换，品质因子可调小波变换概念更简单；利用基为2的快速傅里叶算法，计算更加高效；品质因子和冗余度更容易量化。

信号共振稀疏分解方法利用品质因子可调小波变换分别获取高Q变换与低Q变换的基函数库，并计算其相应的变换系数。可调品质因子小波变换通过带通滤波器组实现，其两通道滤波器组如图2所示。

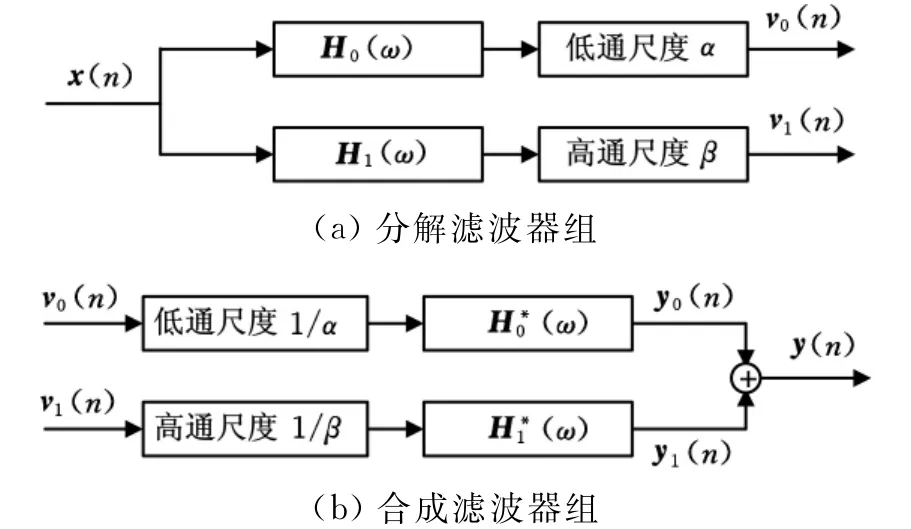
图2 两通道滤波器组

图2 中，β为高通尺度因子为低通尺度因子为冗余度。子带信号v0（n）的采样频率为αfs，v1（n）的采样频率为βfs，其中fs为原信号x（n）的采样频率。

品质因子可调小波变换利用图2a所示两通道分解滤波器组以迭代的方式实现信号的分解，其信号的L层变换如图3所示，其中为信号经过第j层变换得到的高频系数为经过第j层变换得到的低频系数，j＝1，2，…，L。

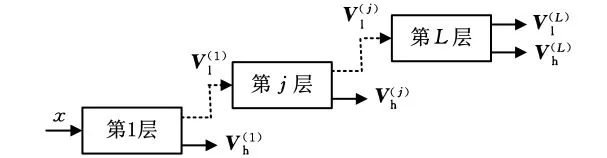
图3 品质因子可调小波变换图

图4 a为品质因子Q＝3、冗余度r＝3、分解层数L＝12时品质因子可调小波变换的频率响应图，从图中可以看出其频率响应为一组非恒定带宽的滤波器组，且相邻频带并不正交。随着分解层数L的增加，中心频率

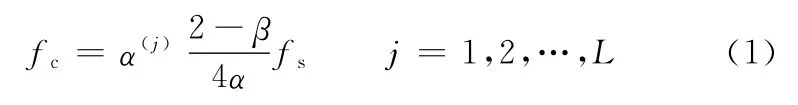
随之降低，相应的带宽

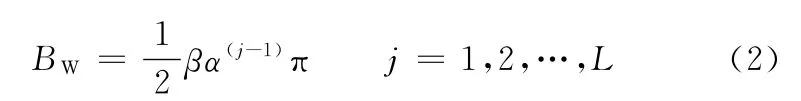
也随之减小。因此，品质因子可调小波变换本质上也为一种具有一定冗余度的恒Q小波变换，但其品质因子可预先设定，并不依赖于基函数。图4b为相应的小波时域波形图，从图中可看出，随着分解层数的增加，小波的振动时间随之变长。

图4 Q＝3、r＝3、L＝12时的品质因子可调小波频率响应与时域波形

1.3 高共振分量和低共振分量的分离

信号共振稀疏分解方法利用形态分量分析［13］将信号中各成分按振荡特性进行非线性分离，建立起高共振分量和低共振分量各自的最佳稀疏表示形式。

假定观测信号x可表示为两个信号x1与x2之和：

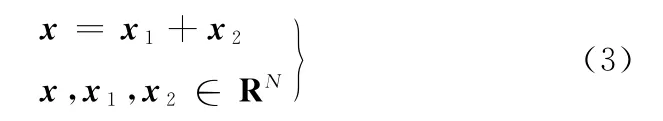
形态分量分析的目的即是从观测信号x中分别估计出源信号x1和x2。假定信号x1和x2可分别用基函数库（或框架）S1和S2表示（S1、S2具有低的相关性），形态分量分析的一种目标函数可表示为式中，W1、W2分别表示信号x1、x2在框架S1、S2下的变换系数矩阵；λ1、λ2为规则化参数。

λ1、λ2的取值对分解出的高共振分量与低共振分量的能量分配有影响，给定λ1、增大λ2会使λ2所对应分量的能量减少；同时增大λ1、λ2的值，则会使残余信号能量增大［9］。

在式（4）中，由于第一范数不可微，且参数较多，使得式（4）的求解变得困难［9］。信号共振稀疏分解方法利用分裂增广拉格朗日搜索算法［14-15］，通过迭代更新变换系数W1、W2，使目标函数J最小化，最终实现高共振分量和低共振分量的有效分离。

假设目标函数J最小时，对应的高共振和低共振变换系数矩阵分别为W＊1、W＊2，则求取的高共振分量和低共振分量的估计值分别表示为

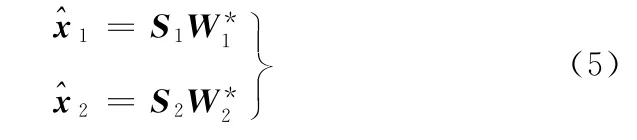
2 信号共振稀疏分解在转子早期碰摩故障诊断中的原理及步骤

当转子系统中出现动静碰摩故障时，由于转子与定子的周期性碰撞，故障信号中常常伴有周期性瞬态冲击。但当出现早期碰摩时，冲击脉冲微弱，淹没在转子自身强背景噪声环境中，不易察觉。信号共振稀疏分解方法根据转子信号中谐波成分与冲击成分品质因子的不同，将转子早期碰摩故障信号分解成包含以转子转频及谐波的高共振分量、包含瞬态冲击成分的低共振分量。由于瞬态冲击信号成分中包含了转子早期碰摩故障的重要信息，因此，可通过对低共振分量中瞬态冲击成分的分析进行转子早期碰摩故障诊断。基于信号共振稀疏分解的转子早期碰摩故障诊断的步骤如下：

（1）根据转子早期碰摩故障信号x，选取高共振品质因子Q1、低共振品质因子Q2（Q1与Q2的相 关 性 公 式 为：ρmax（Q1，Q2） ＝一般取Q2≈1［9］）；高品质因子变换冗余度r1、低品质因子变换冗余度r2（r1、r2一般取3或4即可［12］）；高品质因子变换分解层数L1、低品质因子变换分解层数L2（随着分解层数的增加，对低频段成分的分解将越细微，但计算时间将增加。 最大分解层数公式为信号长度）。本文中取Q1＝4，Q2＝1，r1＝r2＝3，L1＝27，L2＝6。

（2）根据步骤（1）中的参数，分别获取高品质因子可调小波变换与低品质因子可调小波变换的基函数库S1、S2（S1、S2的获取可参考文献［12］），并利用基函数库分别对待分析信号x进行变换，获取初始变换系数W1、W2。

（3）确定规则化参数λ1、λ2（本文中取λ1＝λ2＝0.5）；建立如式（4）所示的目标函数J，利用分裂增广拉格朗日收缩算法估计出最优的变换系数并利用式（5）分别计算高共振分量和低共振分量及残余信号，即信号重构误差

（4）对低共振分量＾x2中的瞬态冲击成分进行分析，根据冲击成分出现的周期即可诊断转子早期碰摩故障诊断。

3 算法仿真

为了验证信号共振稀疏分解方法提取信号冲击成分的有效性，设置如下的冲击信号：

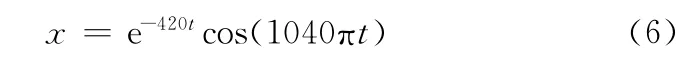
其中，信号载波频率为520Hz，衰减系数为－420。用频率为100Hz的正弦信号对上述冲击信号进行调制，即冲击之间的时间间隔T＝0.01s，采样频率为4096Hz，采样点数为2048，时长为0.5s，调制出的周期冲击信号的时域波形如图5a所示，相应的频谱如图5b所示。

对图5a所示的周期冲击信号加入频率分别为440Hz、680Hz，幅值均为0.4的正弦信号（对比图5b可知，此时冲击信号与正弦信号频率相互重叠），得到的合成信号时域波形如图6所示，从图中可以看出，冲击信号已被淹没。

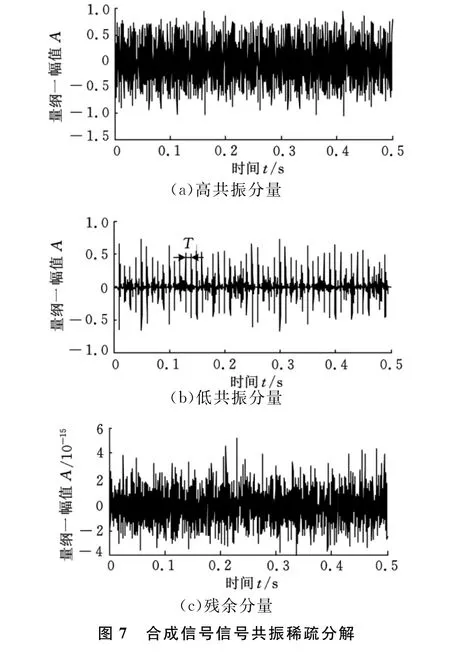
用信号共振稀疏分解方法对图6所示的合成信号进行信号共振稀疏分解，得到的分量如图7所示。从图7b中可看出信号中冲击明显，冲击之间的周期T＝0.01s，与调制频率f＝100Hz吻合，验证了算法的有效性。图7c所示的残余分量为原始信号与高共振分量和低共振分量之差，即信号重构误差，可以看出，残余信号能量非常小，表明信号共振稀疏分解方法具有良好的重构性能。

图5 周期冲击信号及其频谱

图6 合成信号

为对比说明信号共振稀疏分解方法提取冲击信号的有效性，利用EMD对图6所示的合成信号进行分解，得到的IMF分量如图8所示。从图8可看出，信号能量集中在前两个IMF中，但冲击成分不明显。其原因为EMD本质上为带通滤波器组，当冲击信号频谱与正弦信号频谱重叠时，无法将冲击信号与正弦信号分离。

图8 合成信号EMD分解分量图

4 应用实例

为验证基于信号共振稀疏分解的转子早期碰摩故障诊断方法的有效性，进行了转子单点碰摩实验。转子碰摩实验装置结构示意图如图9所示，图中采用一个可调间隙的轴承（部件8）来实现碰摩故障的模拟实验。

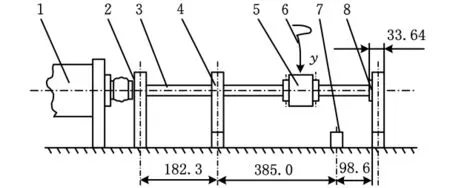
图9 转子碰摩实验装置结构示意图

实验中采用电涡流位移传感器拾取位移信号，转轴工频为3000r／min，采样频率为6400Hz，采样点数为2048。拾取的转子动静碰摩位移信号如图10所示。

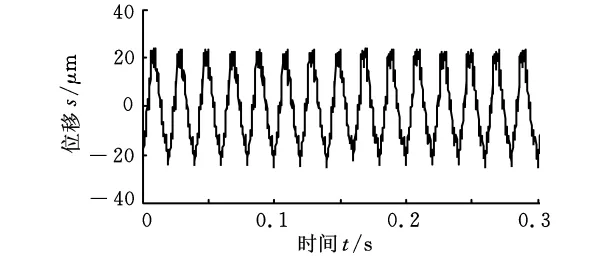
图10 转子动静碰摩振动信号

对转子原始振动信号进行信号共振稀疏分解，得到的分量如图11所示。从图11a中可以看出，信号变化平缓，其主要成分由转频及其谐波信号构成；从图11b中可以看出，信号中存在明显的周期冲击，冲击之间的时间间隔T≈0.02s，冲击出现的频率f＝50Hz，即说明转子每转一圈产生一个冲击，与转子单点碰摩故障特征相符，验证了信号共振稀疏分解方法提取转子碰摩冲击信号的有效性。

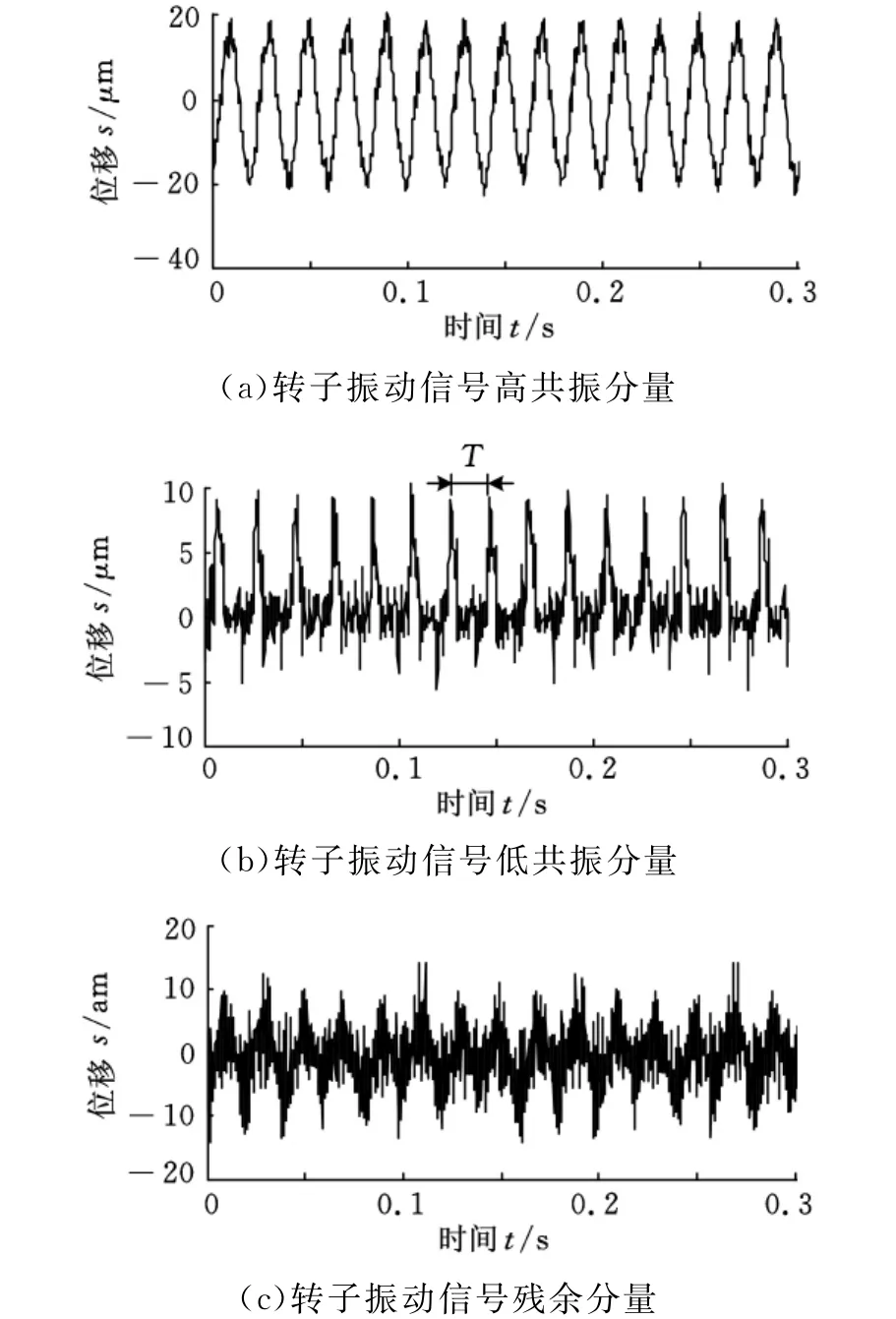
图11 转子动静碰摩振动信号信号共振稀疏分解

5 结论

（1）当转子出现早期碰摩故障时，随着动静件的周期性碰撞，故障振动信号中往往包含瞬态冲击成分，但由于瞬态冲击成分能量较小，常淹没在强背景噪声环境中，不易察觉。

（2）与传统的基于频带划分的信号分解方法不同，信号共振稀疏分解方法根据瞬态冲击与背景噪声品质因子的不同，将信号分解成包含背景噪声的高共振分量和包含瞬态冲击的低共振分量，有效地实现了背景噪声与瞬态冲击的分离。

（3）利用本文方法对实测转子振动信号进行了分析。结果表明，本文方法能有效地提取转子碰摩故障特征。

［1］孙云岭，张永祥，常汉宝.基于定子振动的转子碰摩故障诊断方法研究［J］.振动工程学报，2009，22（4）：391－394.Sun Yunling，Zhang Yongxiang，Chang Hanbao.Method of Rotor Rub－impact Faults Diagnosis Based on Stator Vibration Signal［J］.Journal of Vibration Engineering，2009，22（4）：391－394.

［2］李小彭，姚红良，李鹤，等.质量慢变转子系统的碰摩故障小波分析［J］.中国机械工程，2006，17（14）：1528－1531.Li Xiaopeng，Yao Hongliang，Li He，et al.Wavelet A－nalysis of Rubbing Fault of Slow－varying Mass Rotor System［J］.China Mechanical Engineering，2006，17（14）：1528－1531.

［3］彭志科，何永勇，卢青，等.用小波时频分析方法研究发电机碰摩故障特征［J］.中国电机工程学报，2003，23（5）：75－79.Peng Zhike，He Yongyong，Lu Qing，et al.Using Wavelet Method to Analyze Fault Features of Rub Rotor in Generator［J］.Proceedings of the CSEE，2003，23（5）：75－79.

［4］宋友，柳重堪，李其汉.基于小波变换的转子动静件碰摩故障诊断研究［J］.振动工程学报，2002，15（2）：319－322.Song You，Liu Zhongkan，Li Qihan.Research on Rubimpact Fault between Rotor and Stator Using Wavelet Transform［J］.Journal of Vibration Engineering，2002，15（2）：319－322.

［5］Huang N E，Shen Zheng，Long S R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proceedings of the Royal Society of London A，1998，454：903－995.

［6］Cheng Junsheng，Yu Dejie，Tang Jiashi，et al.Local Rub－impact Fault Diagnosis of the Rotor Systems Based on EMD［J］.Mechanism and Machine Theory，2009，44（4）：784－791.

［7］Flandrin P，Rilling G，Goncalves P.Empirical Mode Decomposition as a Filter Bank［J］.IEEE Signal Processing Letters，2004，11（2）：112－114.

［8］Wu Zhaohua，Huang N E.A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method［J］.Proceedings of the Royal Society of London A，2004，460：1597－1611.

［9］Selesnick I W.Resonance－based Signal Decomposition：A New Sparsity－enabled Signal Analysis Method［J］.Signal Processing，2011，91（12）：2793－2809.

［10］Bayram I，Selesnick I W.Frequency－domain Design of Overcomplete Rational－dilation Wavelet Transforms［J］.IEEE Trans.on Signal Processing，2009，57（8）：2957－2972.

［11］Bayram I，Selesnick I W.Overcomplete Discrete Wavelet Transforms with Rational Dilation Factors［J］.IEEE Trans.on Signal Processing，2009，57（1）：131－145.

［12］Selesnick I W.Wavelet Transform with Tunable Q－factor［J］.IEEE Trans.on Signal Processing，2011，59（8）：3560－3575.

［13］Bobin J，Starck J L，Fadili J M，et al.Morphological Component Analysis：An Adaptive Thresholding Strategy［J］.IEEE Trans.on Image Processing，2007，16（11）：2675－2681.

［14］Afonso M V，Bioucas J M，Figueiredo M A T.Fast Image Recovery Using Variable Splitting and Constrained Optimization［J］.IEEE Trans.on Image Processing，2010，19（9）：2345－2356.

［15］Afonso M V，Bioucas J M，Figueiredo M A T.An Augmented Lagrangian Approach to the Constrained Optimization Formulation of Imaging Inverse Problems［J］.IEEE Trans.on Image Processing，2011，20（3）：681－695. （