小型电子产品流水化生产线设计模型的研究

潘继承，姜雪松*，李东宸

（1.东北林业大学工程技术学院，哈尔滨150040;2.东北林业大学机电工程学院，哈尔滨 150040）

流水线［1］质量的高低直接影响着产品的质量和生产效率，每年因为产线不平衡问题而导致流水线停产检修，严重影响了企业的效益［2］。据不完全统计，仅2009年珠三角地区小型电子产品（Small Size Electronic Products，简称SSEP）制造企业因为产线不平衡问题，导致产品出现质量问题，产线停产，甚至企业倒闭，造成直接经济损失达几十亿元人民币。

采用流水线方式生产的企业，流水线平衡［3］成为一个重要的生产管理问题。流水线平衡问题自1955年Salveson首次提出以来，许多研究人员对此展开了大量的研究，主要可分为精确算法和近似算法两大类，并在不同程度上取得了可喜的成果［4］。

但是流水线平衡问题的根源还是源于流水线最初的设计，只有设计出一条好的生产线，在此基础上才能进行进一步的优化［5－7］。本文将针对HX—118—2型号收音机，结合SSEP流水线本身的特点，在了解收音机内部电子元器件构造的基础之上，通过分析电子元器件装配的优先等级，依据生产计划，得出合理的生产节拍，建立流水线工序分配的运筹学模型，使流水线的各工序之间时间差最小。

1 HX－118－2型号收音机资料收集

收音机的原始资料包括内部电子元器件的组成，需要根据其特点对其分类，见表1。除此之外，同一种类别的电子元器件，也需要根据其自身的不同属性，依据不同的标准，见表2，进行分析和编号分类，见表3。同时，一条流水线的设计还需要产品零件图、装配图、生产工具、产品质量验收标准等。

表1 收音机电子元器件表Tab.1 Electronic components of a radio

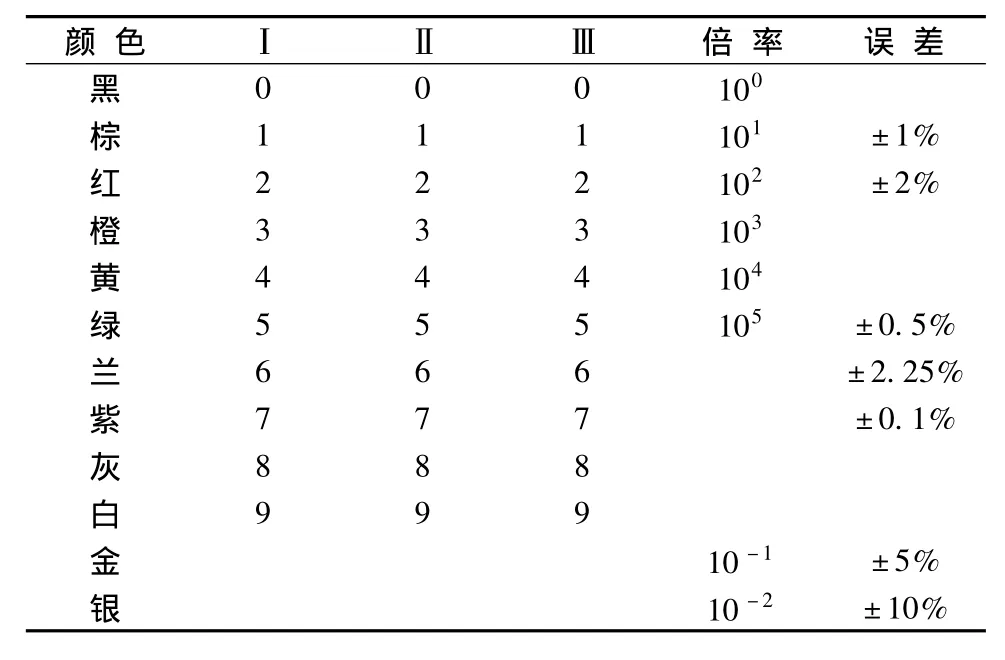
表2 颜色阻值对照表Tab.2 The color of different electric resistivity

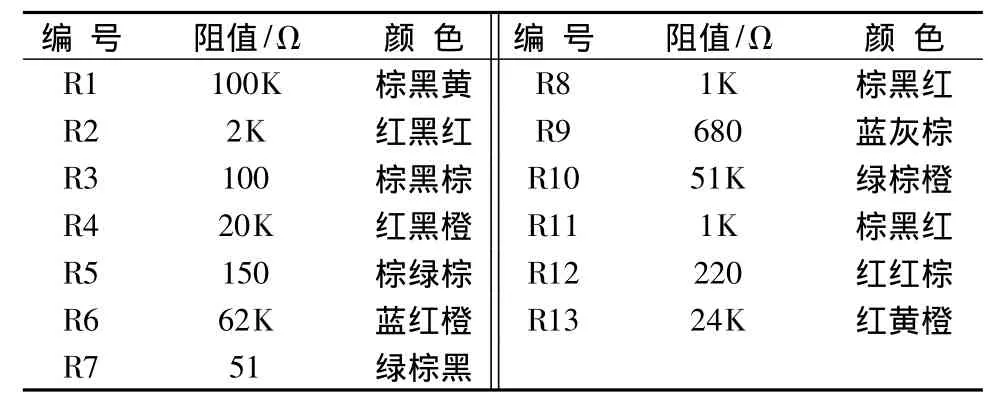
表3 电阻编号表Tab.3 The numbering of different electronic resistivity

2 数据分析与建立模型

2.1 确定流水线的节拍

节拍的长短由计划期的产量和计划其有效工作时间的长短来决定［8］。计划期产品产量包括计划期出产量（合格品）、预计废品量和储备量的变化量。本文计划收音机流水线的计划日产量为900件，每天工作8 h，采用两班制生产，每班停休20 min，计划废品率为2%，则:

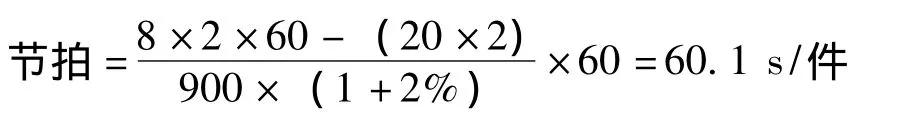
2.2 确定装配元件的优先等级

参照收音机的装配说明书，分析产品内部电子元器件的构造，根据元件尺寸大小和其他装配准则，确定元器件的装配优先级。电子元件编号见表4，装配优先等级如图1所示。

表4 电子元件编号表Tab.4 The numbering of different electronic components

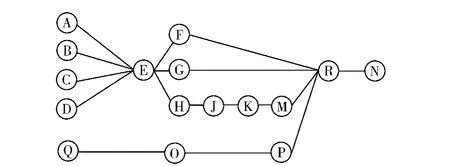
图1 装配优先图Fig.1 The priority of assembling

2.3 计算生产节拍

在产品实际投入生产之前，我们无法知道每个步骤所需要的时间，就需要利用模特法［9］预先估计出装配每一个电子元件所需的时间作为参考。各元件装配时间见表5。

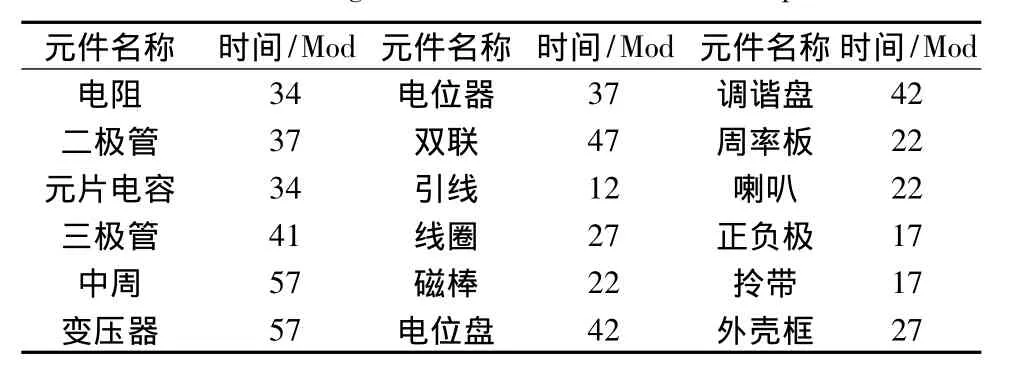
表5 装配时间表Tab.5 Assembling time of different electronic components

由于模特法估计出来的时间在实际中根本无法达到，必须考虑宽放，设宽放率为30%，即参考时间=估算时间×1.3。前面确定的生产节拍为60.1 s，所以单个大工序的时间约为60/0.129=465Mod。依此时间对个小工序进行线性组合，建立线性规划的模型，合成单个大工序。

2.4 模型的建立

运筹学模型一般包含三个组成要素:

（1）决策变量，指决策者为实现规划目标采取的方案措施，是问题中要确定的未知量。

（2）目标函数，指问题要达到目的的要求，表示为决策变量的函数。

（3）约束条件，指决策变量取值时受到的各种可利用资源的限制，表示为含决策变量的等式或不等式［10］。

在本文中，需将不同的电子元器件分配到不同的工序去完成，每个工序所需要完成的电子元器件的个数为决策变量，设xiyi为第yi个工序所需要完成的第i个元件的个数;ai为完成一个i元件装配所需要的时间，ai为已知量;yi为进行第i种元件装配所在的工序数。

首先需要确定目标函数，每个工序的时间越小越好，但是完成原件装配的总时间加在一起是不变的，即工序越多每个工序的时间就越小，但是工序过多会需要较多的工人，我们要求的是在有限的工序里，通过合理的分配，使在所有工序中时间最长的那个工序的时间越短越好，这样完成单个产品的时间就会缩短。设T为单个工序的时间，则目标函数为

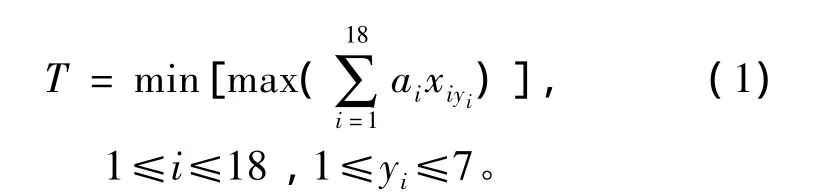
对于单个大工序，它的时间大约为465Mod，对此我们进行约束，它的所有单个大工序时间都不能超过465Mod，即

元件的装配是有先后顺序的，如果装配的先后顺序混乱将造成最后有的元件由于大小或其它问题无法装配。由于同种电子元件的个数不止一个，所以可能将分配在多个工序中进行装配，所以设yim表示集max{yi}，即yi的最大值，则由优先图可得y1≤y5;y2≤y5;y3≤y5;y4≤y5;y5≤y6;y5≤y7;y5≤y8;y8≤y9;y9≤y10;y10≤y11;y11≤y12;y12≤y13;y11≤y12;y13≤y18;y6≤y18;y7≤y18;y17≤y15;y15≤y16;y16≤y18;y14≤y18;y15≤y16。

在很多实际问题中，全部或部分变量的取值必须是整数，如人或机器设备等不可分割。在本文中，电子元件是不可分割的，所以个数必须取整数，工序之间是相互独立的，所以也都必须取整数，即i、yi、xiyi为整数。

2.5 模型的求解

目标函数和约束条件共同构成了生产排产的模型，可以进行人工计算求解，也可以利用计算机软件求解。人工计算求解计算量是比较大的，计算准确度和精度不够好，但求解思路很明晰简单;利用计算机软件求解，如Lingo，求出的解准确度和精度比较好，但需要有较高的软件应用水平［11］。

人工计算法:约束条件不等式限定了装配的先后顺序，基于优先图，可先初步划分各个工序所分配的装配元件组合，只要时间是在465Mod以内都是合理的，然后从所有工序时间中找出时间最大的工序，将其所要装配的元件中的一部分分配到工序时间较小的工序中，但分配的元件装配顺序必须要满足优先图。然后再找出工序时间最长的工序，再进行拆分、分配，循环的进行，直至各工序时间相差不多，这样元件的分配就排出来了，这样得出的结果一直在向最优逼近。基于Lingo软件的求解:使用Lingo软件求解运筹问题可以分为两个步骤来完成:

（1）根据实际问题，建立模型。

（2）利用Lingo来求解模型，主要是把模型转移成计算机语言，借助于计算机来求解，所以要求必须能够熟练地进行模型编译。

本文将通过人工计算法给出求解的结果，得到最优大工序组合见表6。

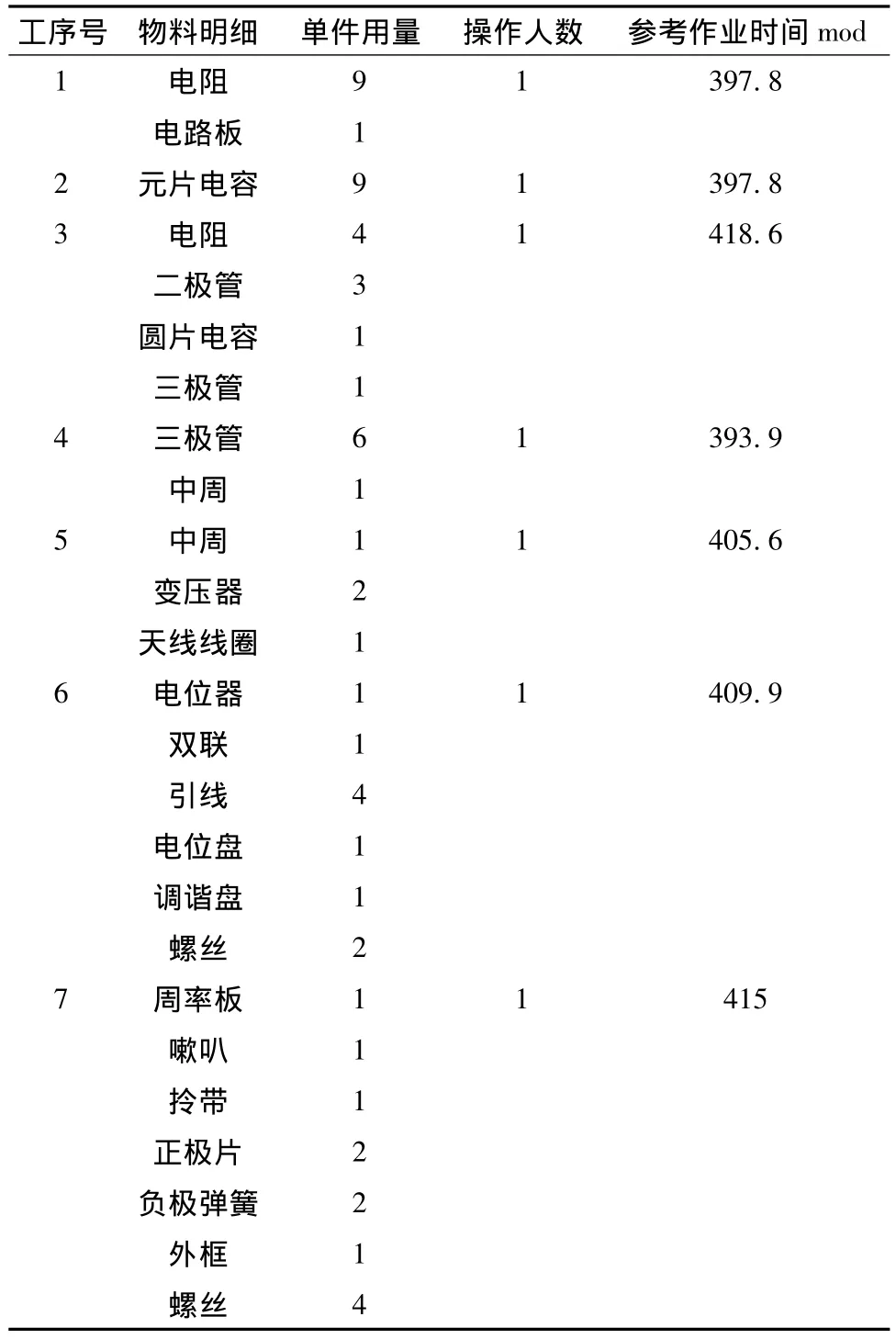
表6 组装顺序表Tab.6 Assembling order

3 模型的检验

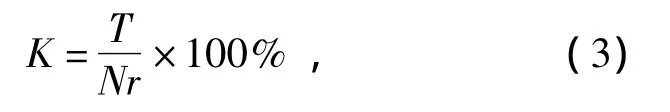
式中:K为流水线负荷系数;T为流水线各工序作业时间之和;N为平衡后流水线实际工作地数;r为节拍。本文中流水线负荷系数K为87.2%。流水线损失时间;

本文中计算出损失时间S为53.72 s。流水线时间损失系数

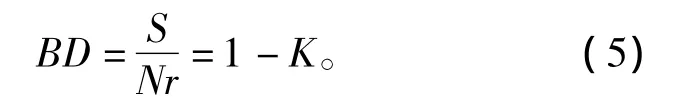
流水线负荷系数:

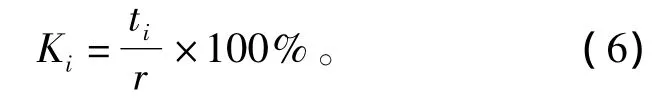
流水线负荷系数决定了流水线作业的连续程度，一般机器工作流水线的负荷系数不应低于75%，以手工为主的装配线限负荷系数不应低于85%。本文中计算出K1=0.86，K2=0.86，K3=0.90，K4=0.85，K5=0.87，K6=0.88，K7=0.89。计算出的Ki均在85%以上，所以流水线作业的连续程度较好。

本文中计算出BD为12.8%。为了评估各工作地效率，还要计算出各个工作地的负荷系数。设第i个工作地作业时间为ti，则该工作地负荷系数Ki为:

4 结论

本文针对SSEP流水线的现状，从产线优化设计角度对产线进行研究，以HX－118－2型号收音机为例，将运筹学模型应用到SSEP流水线的设计之中，得出电子元器件装配的分配工序，使工序间的时间差达到最小，从优化设计角度使流水线获得较高的平衡率。流水线设计中的运筹学模型建立及多元方程的求解方法，为国内现有的以手工操作为主的SSEP流水线设计，提供了理论方法和实践依据。

】

［1］易树平，郭 伏.基础工业工程［M］.北京:机械工业出版社，2007.

［2］罗杰·G施罗德.运作管理［M］.韩伯棠.北京:北京大学出版社，2002.

［3］齐二石.现代工业工程与管理［M］.天津:天津大学出版社，2007.

［4］孙建华，高广章，蒋志强.生产线平衡的手段与方法研究［J］.现代生产与管理技术，2004，21（4）:34 －36.

［5］王 晶，葛安华.液晶显示器装配生产线平衡与优化研究［J］.森林工程，2009，25（1）:28 －32.

［6］包才庆.单一对象流水线的组织设计和应用［J］.林业机械与木工设备，2012，（10）:4055 －4056.

［7］刘家发.新型双齿条差动扎钩装置的应用［J］.林业机械与木工设备，1996，24（4）:29 －30.

［8］甘 凯，李随成，王 锐.某电器公司装配流水线平衡研究［J］.人类工效学，2006，12（3）:36 －38.

［9］郭 伏.模特法在生产线能力平整中的应用［J］.东北大学学报，2003，1（5）:31 －32.

［10］胡运权.运筹学基础及应用［M］.北京:高等教育出版社，2004.

［11］万义国，游小青.优化建模软件Lingo在运筹学中的应用［J］.山西建筑，2007，33（15）:367 －368.