旋转曲面的度量重构＊

章权兵，孙 庆，王 磊，程 鸿

（安徽大学计算智能与信号处理教育部重点实验室，安徽 合肥230039）

1 引言

计算机视觉的基本任务是根据若干幅世界景物的图像求得对真实景物世界结构的理解。因此，三维重构，即由图像恢复场景的三维信息就成了计算机视觉研究的重点和热点问题之一。三维重构问题是一个逆问题，从图像恢复场景的三维形状是一项非常复杂的任务，因为场景几何和摄像机几何都不清楚，而成像过程又丢失了大量信息，导致图像中可用的信息很有限。为了能够得到确定的解，通常需要两幅或多幅图像。例如，在立体视觉中需要通过改变摄像机与场景的相对位置在不同视点下对同一场景分别拍摄两幅图像。然而，如果具有某些先验知识，如场景中的结构信息或者物体具有某种特殊形状等，也可由单幅未标定的图像进行重构，旋转曲面的重构就是其中重要的一类。

旋转曲面是指由一条平面曲线绕一条定直线旋转所形成的曲面，该平面曲线叫旋转曲面的母线，定直线为旋转曲面的对称轴，过母线上任意一点作与对称轴垂直的截面叫旋转曲面的横截面。在日常生活中经常可以见到表面具有旋转曲面形状的物体，如茶杯和古董花瓶等，所以对其研究具有很重要的现实意义。

2003年，Utcke和Zisserman［1］首次提出了单幅未标定旋转曲面的射影重构。随后，Wong等人［2］和Colombo等人［3］分别提出了单幅未标定旋转曲面的度量重构。Wong等人根据旋转曲面的轮廓实现了度量重构，但其在假设摄像机是零扭曲和主点位于图像中心的前提下，只能从单幅图像中计算出摄像机的焦距，重构结果存在单参数的二义性。Colombo等人［4～6］提出了利用射影不变量实现未标定旋转曲面的度量重构，但其在重构过程中，同时考虑了纹理的获取，所以重构过程过于复杂。Wu等人［7］提出了旋转曲面的特殊情况即圆锥体的度量重构，方法简单，但其应用具有一定的局限性。

本文对Colombo等人的重构方法作了改进，对于其中的结构恢复提出了一种新的算法：根据平面透射求出图像中视在轮廓线上每点对应的椭圆（旋转曲面垂直于对称轴的横截面的像），然后利用二次曲线的性质，结合标定出的摄像机矩阵，确定该椭圆对应的旋转曲面横截面（垂直于对称轴，下同）在三维空间中的位置和尺寸，从而恢复整个旋转曲面。该方法重构过程更简单，并能够保持旋转曲面的整体三维结构。

2 基本问题

本文的摄像机模型采用常见的针孔模型：在齐次坐标表示下，任一个空间点Xi与对应的图像点xi之间满足［8］：

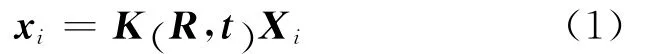
其中，Xi和xi均为齐次坐标，K是摄像机的内参数矩阵，R是3×3旋转矩阵，t是三维平移向量。一般假定摄像机的扭曲因子为零且像素是正方形的，因此有：

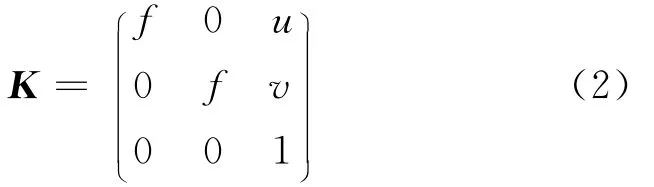
三维重构就是由图像点坐标xi来恢复三维点Xi和摄像机参数。这是一个病态逆问题，通常需要多幅图像来求解，并且在没有其它信息的情况下，重构结果会相差一个射影变换，从而会有无数组解。然而，如果具有某些先验知识，如场景中的结构信息或者物体具有某种特殊形状等，也可以由单幅未标定的图像进行三维度量重构，即重构结果相差一个相似变换。

本文主要针对具有旋转曲面结构的物体进行研究，利用其特殊结构，考虑由单幅未标定的图像进行三维度量重构的问题。重构主要分两步：摄像机标定和结构恢复。摄像机标定利用文献［4］中基于旋转曲面不变量的方法，关于结构恢复本文给出了更简单的算法。

3 摄像机标定

摄像机标定是实现三维度量重构的关键步骤之一。目前，摄像机标定方法的研究主要集中于利用场景中的约束条件，如直线、平面之间的平行和正交关系等。本文先利用文献［4］中基于旋转曲面不变量的方法求出无穷远直线的像l∞和旋转曲面对称轴的像ls，并标定出摄像机的内参数矩阵K。然后按照下面的方法确定摄像机的外参数。

旋转曲面垂直于对称轴的任一横截面为一个圆，我们考虑最下面（或最上面）的圆C。可以根据图像拟合出圆C的像c（实际为一椭圆），进而可利用无穷远直线的像l∞由公式o＝c－1l∞确定出c的中心o的坐标，此即圆C的圆心O的像坐标。

以圆C的圆心O作为世界坐标系的原点，以摄像机中心与对称轴所确定的平面的法线方向为Y轴方向，摄像机中心与无穷远直线的像l∞所确定的平面的法线方向为Z轴方向，与Y轴和Z轴正交的方向为X轴方向建立世界坐标系。

不妨假设在该世界坐标系下，摄像机矩阵为P＝K （R，t）＝K （r1r2r3t），因此圆心O （0，0，0，1 ）T的像为o＝K （r1r2r3t ）（0，0，0，1 ）T＝Kt，从而可得摄像机的平移向量为：

这里所求的平移向量t与实际值可能会相差一个全局比例因子。

一条图像直线l确定一个过摄像机中心的平面，在摄像机坐标系下，该平面的法线方向是n＝KTl，所以得到Y轴的方向为：

同理，Z轴方向的方向为：

由于R是正交矩阵，所以r1＝r2×r3。然后对r1、r2、r3归一化得：

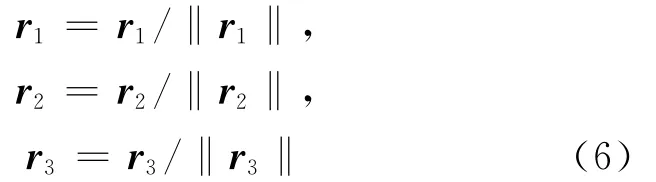
这就得到了摄像机旋转矩阵R和平移向量t，再结合内参数矩阵K即可确定摄像机矩阵P。

4 结构恢复

旋转曲面是由一条平面曲线（母线）绕一条对称轴旋转所形成的曲面，因此为了确定旋转曲面的三维结构，仅需确定旋转曲面的母线和对称轴即可，离散后就是对旋转曲面的母线上任一点X，确定其在所设定的世界坐标系下的高度及其到对称轴的距离。为此，我们对图像视在轮廓线β（光滑曲面的极值边界线在像平面的投影）上任一点x，先确定其对应横截面的像，再利用已获得的摄像机矩阵确定对应横截面的三维坐标，从而获得点x对应的空间点X的高度及其到对称轴的距离。

4.1 横截面的像

为了确定图像视在轮廓线上任一点x对应的横截面的像c，需要先确定一个横截面的像作为参考。对于一般的旋转曲面，可以通过边缘检测再拟合椭圆的方法从图像中直接得到，这里设为c1（如图1所示）。

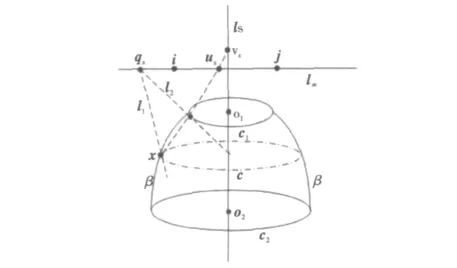
Figure 1 Projective property of the image of revolution surface图1 旋转曲面像的射影性质

旋转曲面有一个非常重要的性质［8］：对于任意两个横截面（圆）的像c1和c，总存在一个平面透射，使得：

其中，l∞为无穷远直线的像，对应平面透射G的轴（由不动点组成的直线），vx是平面透射G的顶点且位于对称轴的像ls上（该直线上的不动点），E是3×3单位矩阵，μ被称为特征不变量，它是不同特征值与重复特征值的比率。

摄像机内参数标定中已经给出无穷远直线的像l∞，因此要求c与c1之间的平面透射G，关键是要确定平面透射G的顶点vx和特征不变量μ。为此，先过点x做一条直线l1与l∞相交于qx，再过qx做椭圆c1的切线l2，假设切点是x1，然后过x和x1做一条直线与ls相交于vx，与l∞相交于ux（如图1所示），则vx即为平面透射G的顶点，vx、ux、x和x1的交比即为平面透射G的特征不变量μ。

根据上述方法，对图像的视在轮廓线上任意一点x，只要有一个参考横截面的像c1，就可确定x所对应的旋转曲面横截面的像c的平面透射G，从而得到对应x的横截面的像为c＝G－Tc1G－1。

4.2 横截面恢复

在确定了摄像机矩阵P和视在轮廓线上任一点x对应的横截面的像c之后，只要求出旋转曲面对应的横截面（边界）C的高度h和半径r，就可实现旋转曲面的度量重构。

在摄像机矩阵P作用下，二次曲线c反向投影成锥面［8］：

该锥面是一种退化的二次曲面，在齐次坐标下可用一个4×4对称矩阵表示，设其矩阵形式为：

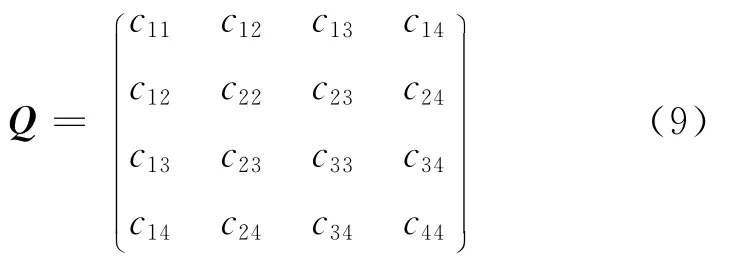
与锥面Q对应的旋转曲面的横截面C即为Q与Z＝h平面的交线（实际上是圆），它满足：

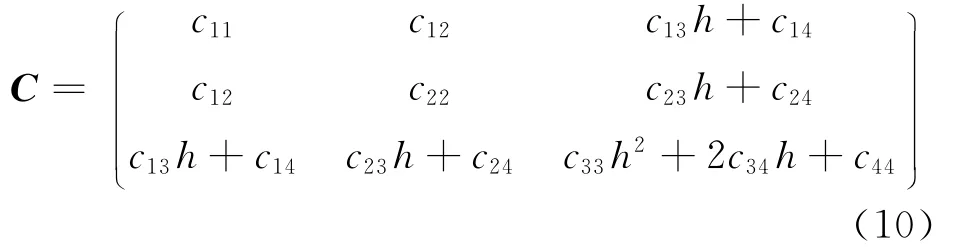
圆C的圆心坐标是OC＝ （0，0，h，1 ）T，其对应的像为oC＝c－1l∞，因此有：

由于oC、K、r3、t均为已知，因此由（11）式即可获得横截面C的高度h。将其代入式（10）便可确定圆C的方程及其半径r。

4.3 算法小结

由单幅未标定的旋转曲面的图像重构旋转曲面的三维结构的具体步骤如下：

（1）从旋转曲面的图像中拟合出两个椭圆c1、c2（旋转曲面横截面的像），同时将旋转曲面的视在轮廓线离散化得到其上若干个点xi（i＝1，…，n）；

（2）利用椭圆c1、c2的交点求出旋转曲面在像平面上的不变量，再利用这些不变量对摄像机进行标定（按第3节方法求出摄像机的内参数K及外参数R和t）；

（3）选择拟合的椭圆c1作为参考椭圆，并结合得到的不变量，按4.1节方法确定过视在轮廓线上的点xi（i＝1，…，n） 的椭圆ci（旋转曲面横截面的像）；

（4）对每个椭圆ci，按4.2节方法确定与其对应的圆Ci（旋转曲面的横截面）的高度和半径，从而得到整个旋转曲面的三维结构。

5 实验

为了验证所给算法理论的正确性，分别用模拟与真实场景进行了实验验证。

5.1 模拟实验

首先模拟产生摄像机矩阵和旋转曲面，将其投影到一幅图像上，并对图像点人为地加上已知方差的零均值的高斯噪声，然后利用所给重构算法恢复出旋转曲面。再将恢复结果反投影到对应的图像上，与原来的图像点坐标相比，求出重投影误差。对不同水平的高斯噪声分别运行100次，重投影误差的均值如图2所示。

Figure 2 Error analysis图2 误差分析

5.2 真实图像实验

图3 是实际拍摄的一幅大小为375×500像素的未标定的花瓶原图像，及拟合出的两个椭圆c1和c2及视在轮廓线（‘＋’）。

Figure 3 Fitted ellipse and points on apparent contour line图3 拟合的椭圆及提取的视在轮廓线上的点

首先，用这两个椭圆c1、c2求出旋转曲面在像平面上的不变量，并利用这些不变量对摄像机进行标定，得到摄像机的内参数和外参数分别为：

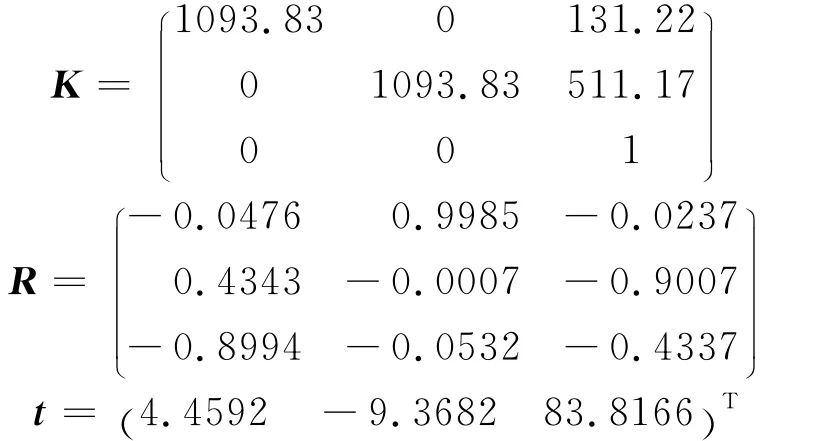
其次，以c1为参考椭圆，由平面透射求出过视在轮廓线上点xi（i＝1，…，n） 的旋转曲面横截面的像ci，结果如图4所示。

Figure 4 Image of cross section of the revolution surface图4 旋转曲面横截面的像

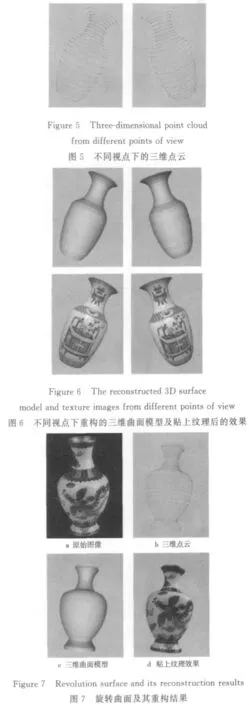
最后再由ci重构得到与之对应的旋转曲面的横截面Ci，从而获得整个旋转体的三维结构。图5显示不同视点下重构的三维点云，图6显示不同视点下的三维曲面模型及贴上纹理后的效果。图7给出另一旋转体的重构结果，左起依次为原始图像、重构的三维点云、重构的曲面模型及贴上纹理后的效果。

6 结束语

本文改进了Colombo等人提出的单幅未标定的旋转曲面三维度量重构的算法。在其算法中，利用不变量重构出旋转曲面表面的三维点，但由于误差的存在，使本来应该位于同一横截面上的点不在同一横截面上。本文所提算法利用二次曲线的性质，直接重构出旋转曲面的横截面，算法简单并且更好地保持了旋转曲面的整体结构。模拟和真实图像实验结果验证了算法的正确性和有效性。

［1］ Utcke S，Zisserman A.Projective reconstruction of surfaces of revolution［C］∥Proc of the 25th DAGM Symposium on Pattern Recognition，2003：265－272.

［2］ Wong K－Y K，Mendonca P R S，et al.Reconstruction of surfaces of revolution from single uncalibrated views［J］.Image and Vision Computing，2004，22（10）：829－836.

［3］ Colombo C，Bimbo A D，Pernici F.Uncalibrated 3Dmetric reconstruction and flattened texture acquisition from a single view of a surface of revolution［C］∥Proc of the 1st International Symposium on 3DData Processing Visualization and Transmission，2002：277－284.

［4］ Colombo C，Bimbo A D，Pernici F.Metric 3Dreconstruction and texture acquisition of a surface of revolution from a single uncalibrated view ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（1）：99－114.

［5］ Colombo C，Comanducci D，Bimbo A D.Camera calibration with two arbitrary coaxial circles［C］∥Proc of the 9th European Conference on Computer Vision，2006：265－276.

［6］ Colombo C，Bimbo A D，Pernici F.Image mosaicing from uncalibrated views of a surface of revolution［C］∥Proc of the 15th British Machine Vision Conference，2004：407－416.

［7］ Wu Yi－hong，Wang Guang－hui，Wu Fu－chao et al.Euclidean reconstruction of a circular truncated cone only from its uncalibrated contours［J］.Image and Vision Computing，2006，24（8）：810－818.

［8］ Hartley R，Zisserman A.Multiple view geometry in computer vision［M］.Cambridge：Cambridge University Press，2000.