用径向基函数Galerkin法解一维稳定流问题

付 鑫，余震果

(辽宁师范大学数学学院，辽宁大连 116029)

用径向基函数Galerkin法解一维稳定流问题

付 鑫，余震果

(辽宁师范大学数学学院，辽宁大连 116029)

将径向基函数引入Galerkin法构成了RBF Galerkin法，该方法近似函数建立在随机分布节点上，无需借助网格，克服了传统方法对网格的依赖。将其应用于一维地下水稳定流问题，推导计算的基本原理，编制相应的计算程序，将计算结果与精确解进行比较，结果表明该方法实用性强，计算精度高。

径向基函数;Galerkin法;一维稳定流

目前，有限元法和有限差分法已成为地下水领域解决工程问题的主要方法，但它们都需要进行初始网格剖分和重构，对网格依赖性强，网格好坏直接影响求解结果。而RBF Galerkin法可以很好地克服这类问题。该方法只需要背景网格，网格只用于数值积分的计算。因此在处理地下水流问题时与其他方法相比，具有计算精度高、稳定性好且易于实施等优点。本文用RBF Galerkin法解一维地下水稳定流问题，推导了计算的基本原理，用MATIAB程序实现该算法，并将计算结果与精确解进行比较。

1 用径向基函数Galerkin法解一维稳定流问题

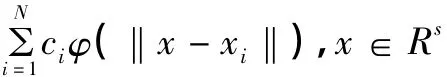
(其中:N表示节点总数，ci为待定系数)。

考虑如下一维地下水稳定流问题

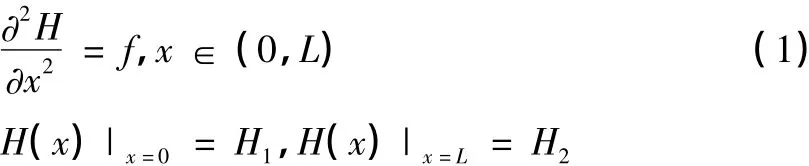
其中:H为地下水水头，f为源汇项。

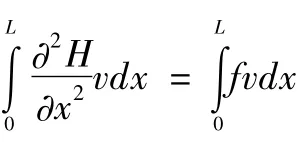
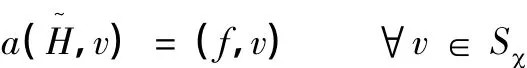
取 χ ={x1，x2，…xN} 取，用N个节点xj(j=1，2，…N) 把求解区域 I离散，其中 x1，x2，…xN－2为内节点，xN－1，xN为边界节点，将水头值函数H(x)的近似解(x)用试探函数

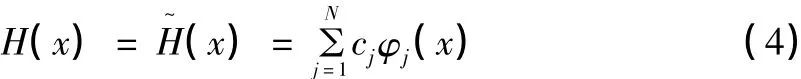
表示，其中N为节点总数，cj为待定系数，φj(x)为以各节点xj为中心的径向基函数。

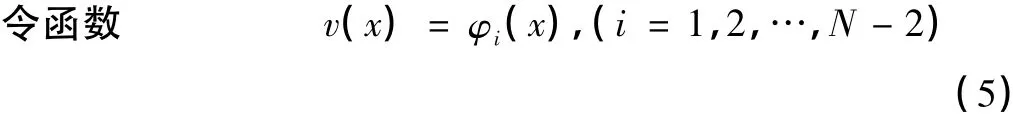
把(4)、(5)两式代入(2)式，整理得

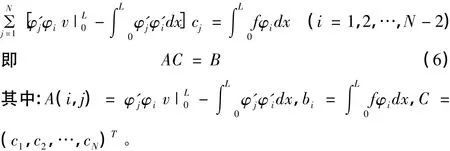
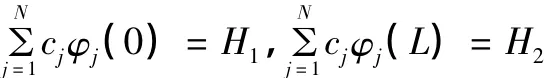
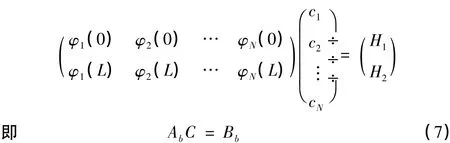
将(6)、(7)两式联立写成矩阵方程

通过式(8)解出 C即 cj，将其代入式(4)，得到近似解(x)。

2 承压含水层稳定流问题

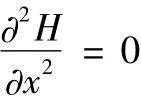
将研究区域［0，100］进行10等分，即N=11。用MATLAB编制相应程序，选取Gaussian径向基函数为近似函数，通过试验获得最佳参数ep，得到了比较精确的结果，图2为精确解与近似解的对比。

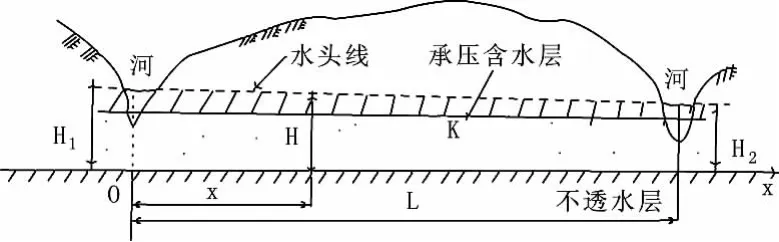
图1

图2

3 非承压含水层稳定流问题

如图3所示，一均质、等向非承压含水层，渗流区的上边界为断面线Ⅰ，已知水头h1=10 m，下边界为断面线Ⅱ，已知水头h2=7 m，渗透系数K=0.864 m/d，L=100 m，并且在区域内满足

图4为非承压含水层中地下水向河、渠稳定流动时精确解与近似解的对比。

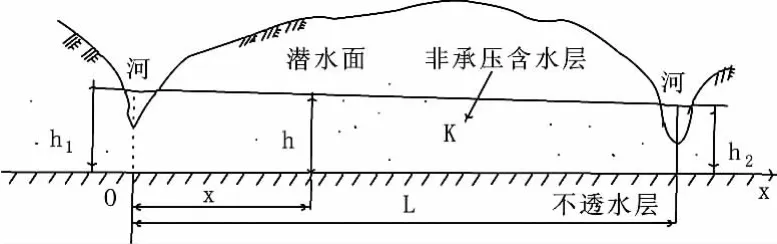
图3

图4

4 有垂直补给非承压含水层稳定流问题

如图5所示，一具有水平不透水底层，且有降雨补给ε=0.004 m/d的非承压含水层，上边界为断面线Ⅰ，已知水头h1=10 m，下边界为断面线Ⅱ，已知水头h2=7 m，渗透系数K=0.864 m/d，L=100 m，并且在区域内满足

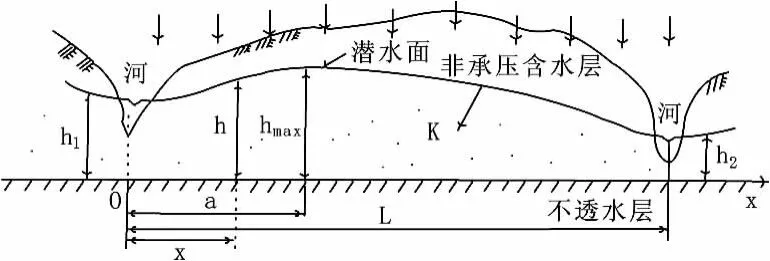
图5

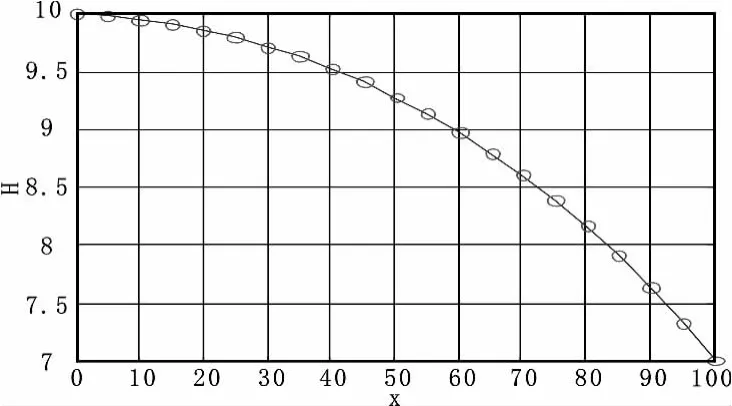
图6

5 结语

本文的方法及应用显示了由径向基函数与无网格伽辽金法相结合构成的径向基函数Galerkin法的适用性与合理性。实验结果令人满意，表明该方法是一种计算精度高且有效的求解方法，在工程中具有广阔的应用前景。今后的进一步工作将着眼于径向基函数Galerkin法的推广应用，使其适用于地形复杂的二维地下水流问题。

［1］Wendland H.Meshless Galerkin method using radial basis functions［J］.Math.Comput.，1999，68(228):1521 －1531.

［2］张雄，陆明万，Wegner J L.A 2－D meshless model for jointed rock structures［J］.Int.J.Num.Meth.Engng.，2000，47(10):1649 －1661.

［3］Zhu T，Atluri S N.A modified collocation method and a penalty formulation for enforcing theessential boundary conditions in the element free Galerkin method［J］.Comput.Meth.，1998，211 － 222.

［4］Ventura G.An augmented Lagrangian approach to essential boundary conditions in meshless methods［J］.Int.J.Num.Meth.Engng.，2002，53:825－842.

［5］Belytschko T，Lu Y Y，Gu L.Element free Galerkin methods［J］.Int.J.Num.Meth.Engng.，1994，37:229 －256.

［6］张雄，刘欣，陆明万等.Imposition of essential boundary conditions by displacement constraint equations in meshless methods［J］.Comm.Numer.Methods Engrg.，2001，17(3):165－178.

Application of RBF Galerkin Method in One－Dimensional Steady Flow Simulation Model

Fu Xin，Yu Zhenguo
(School of Mathematics，Liaoning Normal University，Dalian116029，Liaoning)

As a combination of radial basis function and Galerkin，RBF Galerkin method can be used without internet by building its approximation function on a series of notes.By using RBF Galerkin method，the paper deduces formula and computation program of one－dimensional steady flow simulation model.Comparison of result got from the new method and exact solution indicates that RBF Galerkin method is widely applicable and considerably accurate.

RBF，Galerkin method and one－dimensional steady flow

P641.12

A

1004－1184(2013)05－0029－03

2013-05-13

付鑫(1989-)，女，辽宁阜新人，在读硕士研究生，主攻方向:偏微分数值解法研究。