长三角制造业劳动生产率空间差异研究——基于ESDA分析的证据*

柯 蓉 秦 莉

一、引言

长三角是我国经济发展速度最快、经济总量规模最大、最具有发展潜力的区域。其中长三角地区制造业产值占全国制造业总产值的四分之一以上。在整个长三角地区经济取得巨大成就的同时，在区域内部各城市之间的经济却存在着一定的差异。通过大量文献及整理近10年来长三角地区等经济指标的数据，可以初步发现长三角地区整体的经济发展水平的分布格局呈现较为明显的中心到外围的格局。经济发展较快的主要集中在长三角的中部，如上海、苏锡常地区，而经济发展对缓慢的主要集中在长三角地区的边缘地带，如扬州、台州等地。

范建勇和朱国林（2002）对地区差异的研究表明：1995年以后第二产业基尼系数贡献率超过了60%。在第二产业中占主要地位的是制造业，所以地区差异实际上主要是各地制造业的差距，这一点也与我国正在经历的工业化进程一致。除了各地的工业规模和密集程度外，长三角制造业劳动生产率的空间差异是各地工业生产差异的主要原因。陈建军和夏富军（2006）通过对长三角制造业垂直分工水平的测度，描绘出了长三角内部制造业的产业优势格局。刘录敬和陈晓明（2010）采用行业平均集中率指标和赫芬达尔—赫希曼指数分析了长三角制造业平均集中率和空间集中度，然后以制造业二位数分类行业集中分析了两省（浙江、江苏）一市（上海）产业转移情况。吕新雷等（2010）对长三角制造业空间集聚与扩散进行了实证研究，论述了城市产业转型及发展方向。通过对现有关于长三角地区差距相关研究文献的梳理，可以发现国内多数经济学者都是基于传统的新古典增长理论的分析框架来对长三角地区差距长期动态演变的趋势及成因进行的研究。

关于长三角制造业劳动生产率的差异方面，姚瑶，宁越敏（2009）利用区位商分析方法和计算劳动生产率对2005年长三角制造业的发展层次和空间差异进行了实证检验。同时也指出区位商方法在分析区域产业结构以及空间差异方面的不足之处。本文将采用探索性空间数据分析方法（ESDA）对长三角地区制造业劳动生产率的空间差异以及空间相关性进行定量分析，以期有助于了解长三角地区制造业发展状况的差异、演变态势以及存在的一些问题。

二、研究方法与数据来源

（一）研究方法

本文采用了空间统计分析和描述性统计分析相结合的方法，要进行空间统计分析，首先要确定地区之间相互作用的关系模型，一般通过设定空间权重矩阵来实现这个目的。空间权重矩阵的定义是空间统计学与传统统计学的重要区别之一，是利用ESDA技术进行空间探索分析的前提和基础。如何选择适当的空间权重矩阵是空间数据分析中最难且最有争议的问题之一。

空间权重矩阵的构造方法很多，例如二进制邻接权重矩阵、K最近点权重矩阵、基于距离权重矩阵、Dacey权重矩阵、阈值权重矩阵等。在区域经济研究领域，常用的权重矩阵主要是二进制邻接权重矩阵、基于距离权重矩阵、Dacey权重矩阵等。一般空间权重矩阵的定义方法都与空间单元的物理特征紧密相连，与二进制连接矩阵一样，当空间单元由点构成时，这种定义方法就会失效，而采用的解决办法即利用泰森多边形所确定的边界长度和面积又存在很大程度的主观性。另外，当所考虑的空间相互关系由某些因素如纯粹的经济变量决定，而这可能与地图上的空间边界的结构关系很小时。目前，二进制邻接矩阵因其简便性及适用性，是空间分析学家在进行空间模型分析时首选矩阵。本文选取二进制邻接方法创建权重矩阵。

1.二进制邻接权重矩阵

最初对空间依赖性及空间自相关的测度，是基于空间单元间二进制邻接性思想进行的，邻接性由0和1两个值表达。如果两个空间单元有非零长度的公共边界，就认为二者是相邻的，对应的二进制邻接矩阵的元素赋值为1。这种空间权重矩阵称之为二进制邻接矩阵，元素定义形式如下：

其中，i，j∈［1，n］，i，j均为空间单元编号，n为空间单元个数。

二进制邻接矩阵在空间相邻定义的基础上，进行一定的扩展，定义为基于距离的二进制权重矩阵，表达式为：

其中，d为根据所做研究的需要自定义的距离。这两种矩阵的主要区别在于d是否为0，d为0则是邻接矩阵，d不为0则是距离矩阵。

2.全局Moran’s I指数

全局Moran指数是由Moran于1948年提出的，它反映的是空间邻接或邻近的区域单元属性值的相似程度。全局Moran指数取值范围为［-1，1］，正值表示该空间事物的属性值分布具有正相关性，负值表示该空间事物的属性值分布具有负相关性，0值表示该空间事物属性不存在空间相关，即空间随机分布。计算公式：

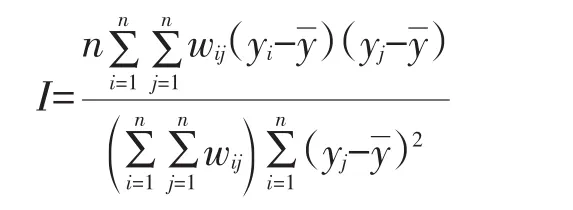
式中，n为格数据目，yi和yj分别是空间对象在第i和第j两点的属性值，y为y的平均值，空间权重矩阵元素wij为空间对象在第i和第j两点之间的连接关系。

对于全局Moran指数，可以用标准化统计量Z（I）来检验空间自相关的显著性水平。Z（I）的计算公式为：Z（I）=（I-E（I））/Var（I），Var（I）是 Moran 指数的理论方差，E（I）=-1/（n-1）为其理论期望。

全局间自相关假定空间是同质的，即研究区域内的空间对象的某一属性值只存在一种整体趋势。但空间对象的空间异质性并不少见。因此需要发展局域统计方法来衡量每一个空间对象属性在局部的相关性质。局域相关性的研究主要是运用局域Moran’s I指数、Moran’s散点图进行衡量。

3.局域Moran’s I指数（亦称LISA）

局域Moran’s I指数是将全局Moran’s I指数分解到局域空间上，即针对空间每一个分布对象，有：

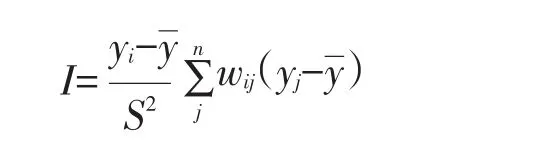
4.Moran散点图

以（Wz，z）为坐标点的Moran散点图常来研究局部的空间不稳定性，对空间之后因子Wz和z数据进行可视化的二维图示。值得注意的是Moran散点图不是LISA，因为其不能获得局部空间集聚的显著性指标。

Moran散点图的四个象限分别对应区域单元与其邻居之间的四种类型的局部空间联系形式：第一象限（HH）代表了高观测值得区域单元被同是高观测值的区域所包围的空间联系形式；第二象限（LH）代表了高观测值得区域单元被低观测值的区域所包围的空间联系形式；第三象限（LL）代表了低观测值得区域单元被同是低观测值的区域所包围的空间联系形式；第四象限（HL）代表了低观测值得区域单元被高观测值的区域所包围的空间联系形式。

与局部Moran’s I指数相比，其重要的优势在于能够进一步具体区分区域单元和其邻居之间属于高值和高值、低值和低值、高值和低值、低值和高值之中的哪种空间联系形式。并且，对应于Moran散点图的不同象限，可以识别出空间分布中存在着哪几种不同的实体。将Moran散点图与LISA显著性水平相结合，可以得到“Moran显著性水平图”，在图中显示出显著的LISA区域，并分别表示出对应Moran散点图不同象限的相应区域。

（二）数据来源

本文所有数据均来源于长三角江苏、浙江、上海16个地级城市的统计年鉴，由于统计口径差异（既包括时间序列上的差异，也包括不同城市间的差异），许多数据都要进行处理后才能保证研究的一致性和可靠性。特别是不同的统计年鉴在同一指标上的数据往往会有不一致的地方。由于2010年以来有些地区的数据有缺失，为保证数据的可比性，本文选取数据时间跨度为2003—2009年。

三、实证分析

（一）长三角制造业劳动生产率描述性统计分析

本文利用长三角16个城市2003年到2009年的制造业销售产值数据，绘制了制造业销售产值的最大值和最小值折线图（如图1），从图1中可以看出长三角制造业在各市之间的差距逐步放大。由2003年10142亿元的增至2009年的21619亿元，增幅达到113.17%。

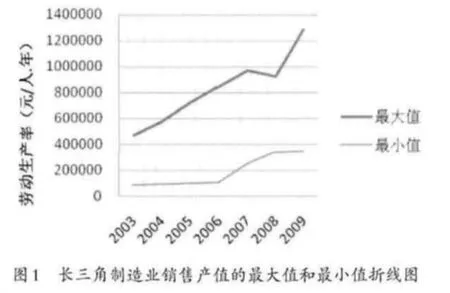
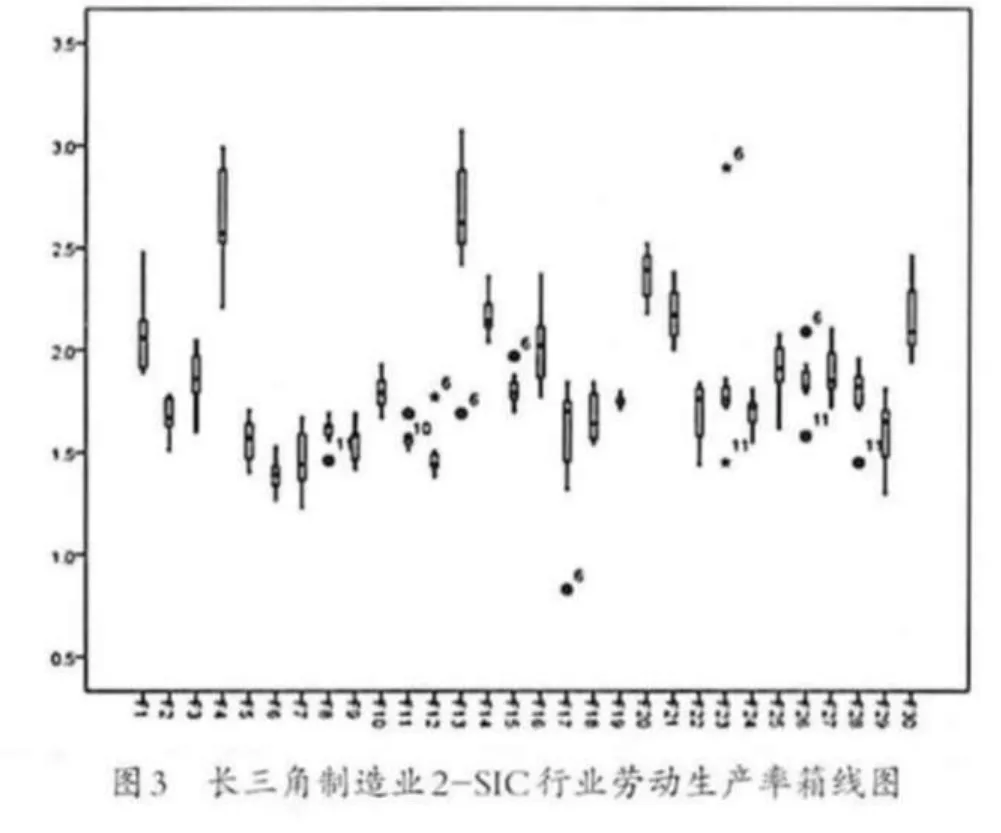
除了各地的工业规模和密集程度外，劳动生产率的差异是各地制造业生产差异的主要原因。根据图2绘制的长三角制造业劳动生产率的最大值和最小值的折线图可以看出，长三角制造业生产效率在各市之间的差异也在持续放大，由2003年的384179（元/人）增至2009年的935340（元/人），增幅达到146.46%。为了更清晰地显示长三角地区制造业生产效率在空间上的差异，本文分别计算整理了2009年长三角地区30个制造业的两位数行业在16个地级市的劳动生产率，并利用其自然对数指绘制了箱线图。

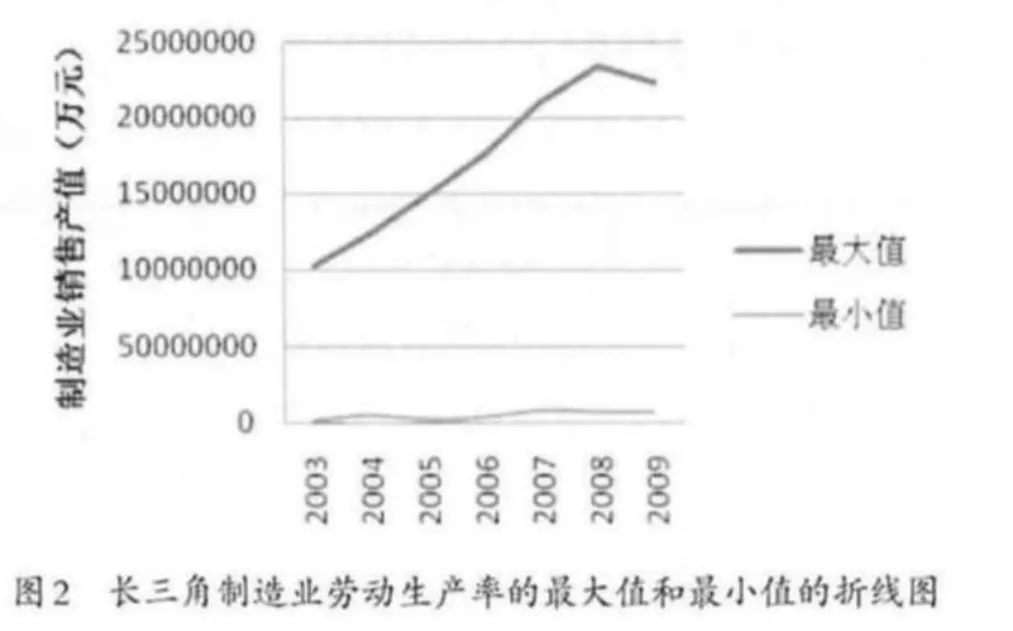
长三角制造业两位数行业的劳动生产率在空间上均显示了明显的差距，而且这种差距在不同的行业间又显出了不同的程度。生产效率在城市层次次上差异较大的行业依次为：烟草加工业（F4）、石油加工及炼焦业（F13）、橡胶制品业（F17）、废弃资源和废旧材料回收加工业（F30）、黑色金属冶炼及延压加工业（F22）和交通运输设备制造业（F25）。

（二）EDSA（探索性数据分析）

通过对长三角区域制造业的初步分析，我们可以了解长三角区域制造业产业集聚整体现状。为进一步了解长三角区域制造业集聚和劳动生产率的空间差异情况，本文基于探索性数据分析方法对其进行对长三角制造业进行纯地理效应研究。

1.权重矩阵的建立

探索性数据分析方法最重要的是权重矩阵的建立。因此在进行相关性分析之前，首要的是创建空间权重矩阵。本文选取二进制邻接方法创建权重矩阵，先将长三角25个城市进行编码，再根据它们与周围城市的地理位置是否相邻，得到权重矩阵。因为舟山在地理上处于孤僻的位置，因此在地理位置得到的二进制邻接矩阵基础上，根据区域间的经济活动往来密切的城市，稍作修改，将其与宁波、上海视为邻居关系。

2.Moran’I指数

全局空间相关性反映了观测值在全部区域范围内集聚的整体趋势，一般用全局Moran’I指数作为统计量进行分析。本文利用Geoda软件，采用2003—2009年间的制造业劳动生产率的数据，得出长三角的全局Moran’I指数，如表1所示：

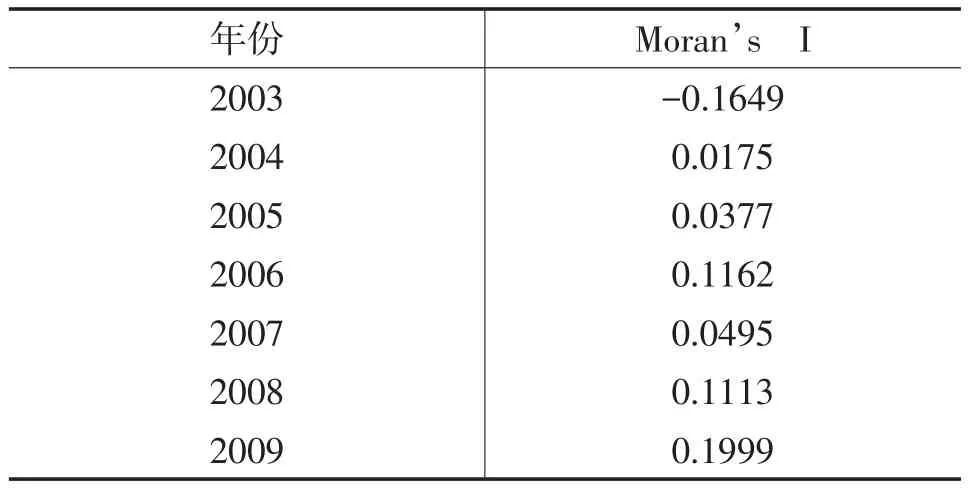
表1 长三角制造业全局Moran’I指数

通过对表进行观察，可以初步得出长三角制造业生产率差异的大体分布。2003年制造业劳动生产率的Moran’I指数小于0，这表示长三角各区域制造业生产率存在负相关，即可能存在生产率高的区域被生产率低的区域包围，或者是生产率低的区域被生产率高的区域包围。从2004年开始劳动生产率的Moran’I指数开始大于0，并逐步增大。这表明长三角区域制造业生产率呈现正相关，即可能存在生产率高的区域逐步集聚在一起，或者是生产率低的区域集聚在一起。不管是哪种情况，都意味着长三角区域相互促进，内部的联系更加紧密，相互影响的作用力更加强大。

3.Moran散点图

空间集聚的全局分析往往会忽略一些局部反常的情况或一些局部不稳定的现象，因此在进行全局分析的同时，需要加入局部空间分析，作为对全局分析的一个补充，以求把握整体空间分布格局，尽可能地避免局部不稳定情况的遗漏。

在此，采用2003年到2009年的制造业劳动生产率数据，通过Geoda软件分析制造业整体劳动生产率的局部Moran’I指数，并得到相应的Moran’I散点图。

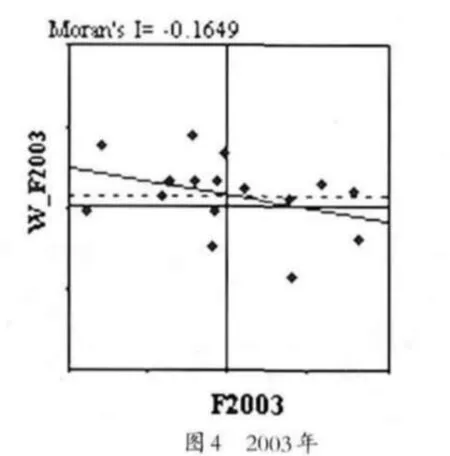
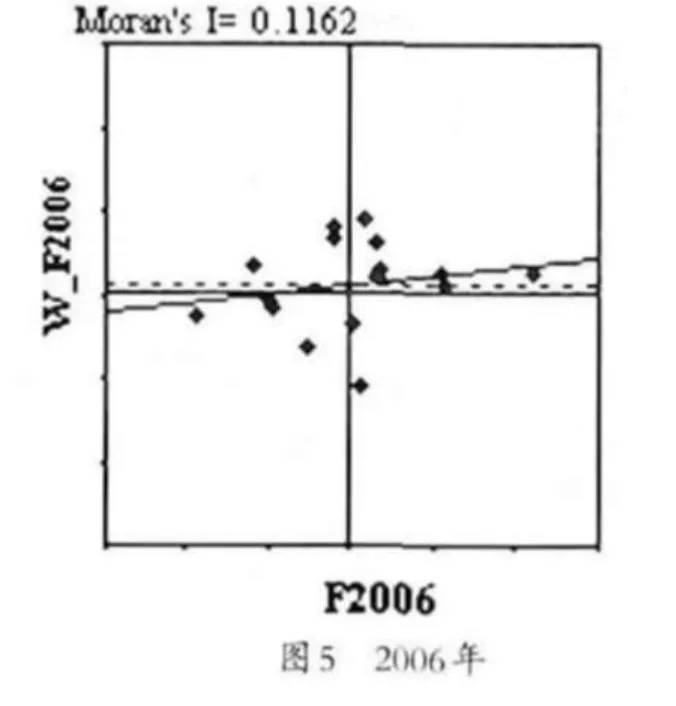
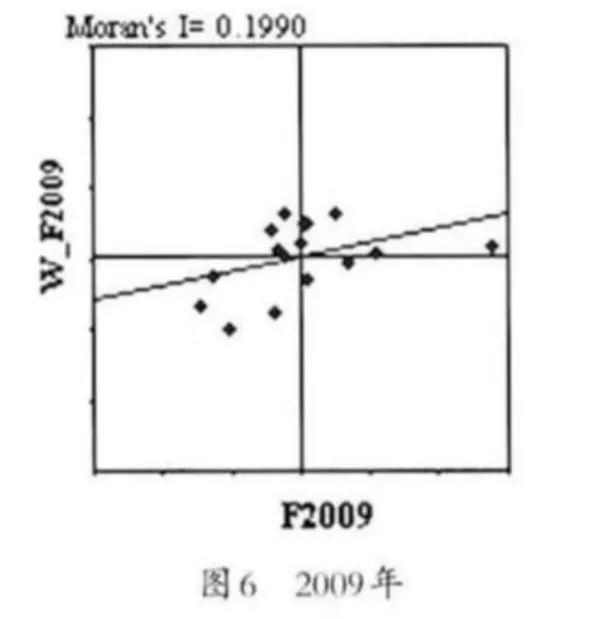
观察2003年的散点图（如图4），可以看出观察值较为分散，而且落在第二象限的居多，而第二象限代表了高观测值的区域单元被低观测值的区域所包围，表明生产率高的区域被生产率低的区域包围。2004年则开始摆脱这种负相关的联系，局部呈现了均匀分布，而从2005年开始所有的观察值都在向中心聚拢，这体现的是很强的空间集聚特征。观察2009年的散点图（如图6），大部分观察值都集中在中心位置，而第三象限中的观察值则增多到4个，并远离中心位置。而第三象限（LL）代表了低观测值的区域单元被同是低观测值的区域所包围的空间联系形式，即生产率低的区域集聚在一起。得出以下结论：（1）长三角制造业劳动生产率所体现出来的空间正相关，并不是效率高的地区在带动效率低的区域，反而是效率低的区域在相互影响。（2）正在逐渐扩大的区域劳动生产率差异也正是效率低的地区聚集在一起，没有突破性的发展。

4.LISA显著性水平图

虽然Moran’I散点图说明长三角各城市间的差距有所缩小，但是Moran’I散点图不能很好地提供区域显著性检验结果，因此利用LISA显著性水平图分析2003年到2009年制造业劳动生产率的数据，得到LISA显著性水平图，可以形象地展示长三角区域经济的空间相关集聚现状。

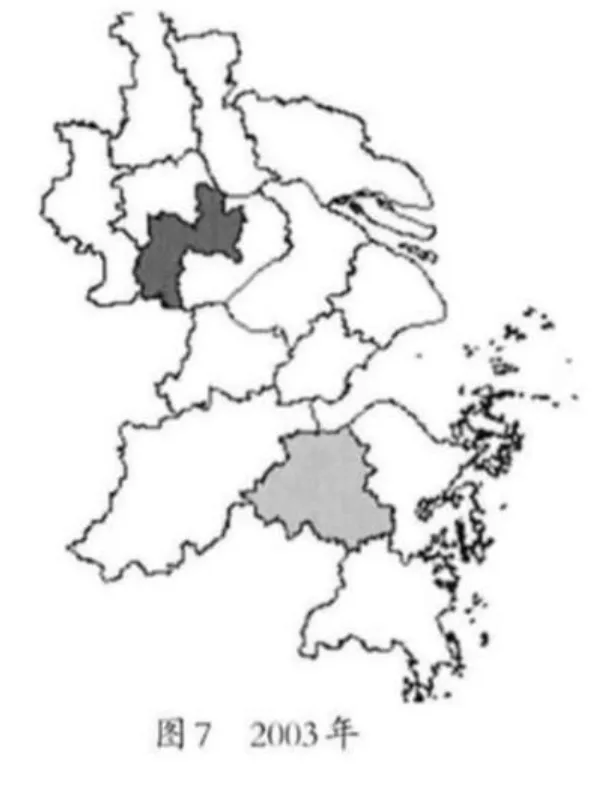
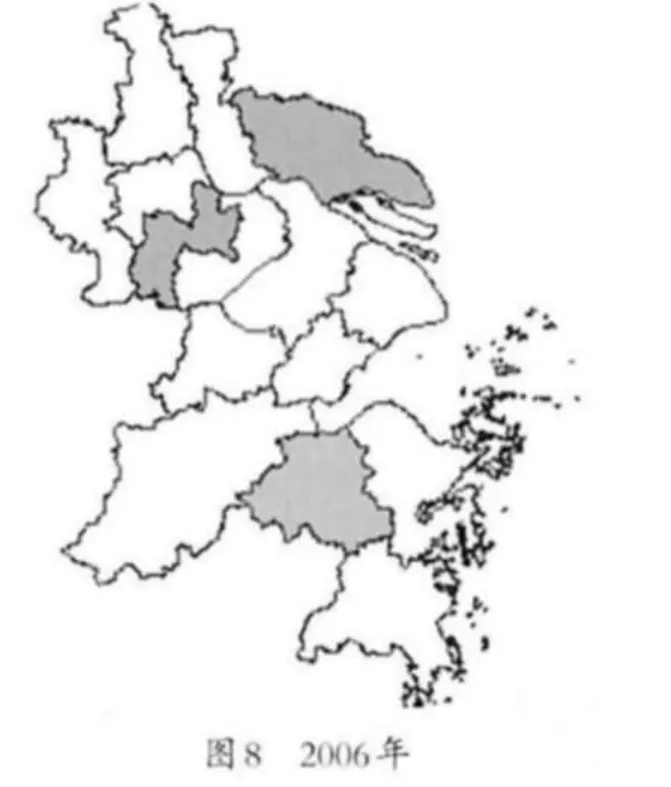
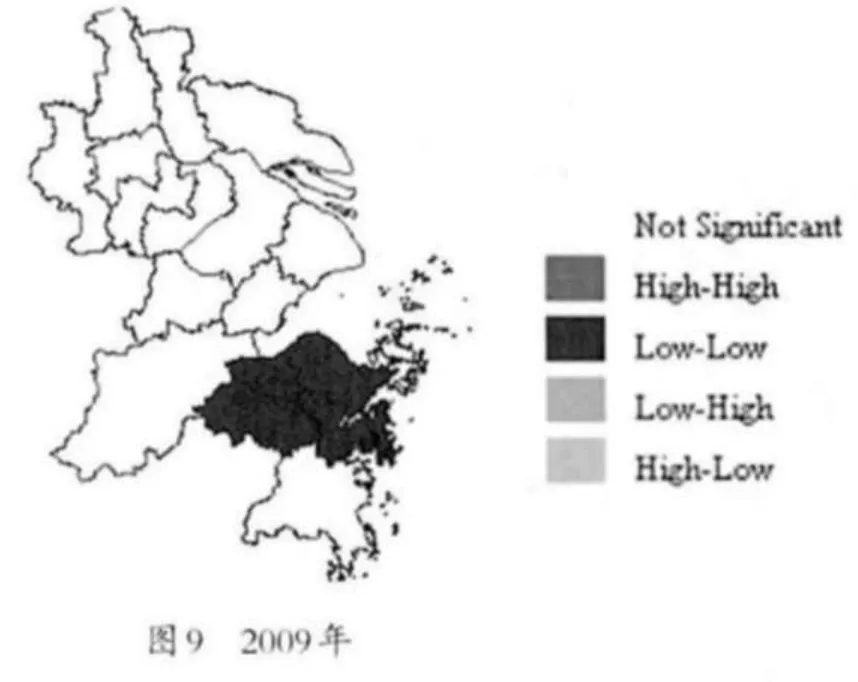
图7至图9形象地展示了2003年和2009年长三角16个城市制造业劳动生产率的Moran空间自相关聚类现象，其中，High-High代表高生产率集聚中心，Low-Low代表生产率集聚中心，Low-High代表低生产率区域被高劳动生产率区域包围，High-Low代表高生产率区域被低劳动生产率区域包围，Not Significant代表区域间劳动生产率没有体现相关影响。

2003年，以绍兴为中心有一个H-L的区域，围绕在其周围的杭州、台州、杭州等地的劳动生产率皆比较低，而其他地方没有出现很明显的集聚现象。2006年，则出现了两个分别以南通和常州为中心的L-H区域。围绕在南通周围的上海、苏州以及泰州的劳动生产率都有了比较大的进步，而南通的驻足不前，就有了如此的非典型性集聚。而围绕在常州周围的南京和无锡区域的制造业劳动生产率在长三角内部皆名列前茅，常州的劳动生产率虽不是很低，但居于其中也就形成了L-H区域形态。到2009年，由于常州在周围高劳动生产率的带动影响下，其劳动生产率也有了较大的增长，首次出现了H-H型集聚。以宁波为中心形成了一片劳动生产率的低洼区域。此后一直保持集聚格局到2009年。

四、结论及建议

本文对长三角制造业劳动生产率进行了Moran's I值、Moran's I散点图和LISA分布图等空间数据分析。结果表明长三角制造业劳动生产率空间差异也在持续放大，其中差异较大的行业依次为：烟草加工业（F4）、石油加工及炼焦业（F13）、橡胶制品业（F17）、废弃资源和废旧材料回收加工业（F30）、黑色金属冶炼及延压加工业（F22）和交通运输设备制造业（F25）。

2003年长三角各区域制造业生产率存在负相关，即存在生产率高的区域被生产率低的区域包围，或者是生产率低的区域被生产率高的区域包围。以绍兴为中心有一个H-L的区域，围绕在其周围的杭州、台州、杭州等地的劳动生产率皆比较低，而其他地方没有出现很明显的集聚现象。从2004年长三角区域制造业生产率呈现正相关，正在逐渐扩大的区域劳动生产率差异也正是效率低的地区聚集在一起，并不是效率高的地区在带动效率低的区域，反而是效率低的区域在相互影响。这时出现了两个分别以南通和常州为中心的L-H区域。围绕在南通周围的上海、苏州以及泰州的劳动生产率都有了比较大的进步，

长三角区域制造业生产率呈现空间正相关，都意味着长三角区域相互促进，内部的联系更加紧密，相互影响的作用力更加强大。整体来看长三角区域制造业发展水平的空间分布与地理位置、资源状况、经济基础紧密相关，同时还与交通、产业结构等有很大关系。制造业生产效率的提升在很大程度上取决于其所处区域产业结构的多样化程度，这种建立在技术经济联系上的产业间相互渗透是目前长三角制造业产业提高劳动生产率的重要环节。因此政府应引导本地产业结构的调整，从区域的单一生产结构向多样化发展。

从产业间的劳动生产率在空间上呈现空间自相关的现象出发，各区域产业之间应该加强联系，放大这种自相关相互促进的效应，从单一产业、单一区域的发展演变成整个制造业、整个长三角地区簇团似的发展。

［1］范建勇，朱国林.中国地区差距演变及其结构分解［J］.管理世界，2002，（2）：45—50.

［2］陈建军，夏富军.垂直分工、产业集聚与专业化优势——兼论长三角地区的制造业优势格局［J］.南通大学学报，2006，（9）：34—38.

［3］刘录敬，陈晓明.长三角制造业产业空间转移实证研究［J］.商业时代，2010，（25）：120—121.

［4］吕新雷，从海燕，魏守华.长三角制造业空间集聚与扩散的实证研究——兼论城市产业转型及发展方向［J］.现代城市研究，2010，（11）：17—22.

［5］姚瑶，宁越敏.长三角制造业发展层次和空间差异研究［J］.中国城市研究（电子期刊），2008，（2）：57—64.

［6］王远飞.空间数据分析方法［M］.北京：科学出版社，2007.