基于Optistruct的重力坝拓扑优化应用研究

何成龙，涂兴怀

（西华大学能源与环境学院，四川 成都 610039）

工程结构优化是随着计算机技术和有限元技术的发展而迅速发展起来的，目的是使工程结构更加稳定，体积或材料分布达到最优，使结构在满足刚度和耐久性等要求的同时，组件更加轻量化。工程结构优化类型主要包括拓扑优化、尺寸优化和形状优化等几类。尺寸优化作为工程结构优化中最低层次的优化类型，主要是通过调整结构的几何尺寸使构件的结构达到最优。形状优化一般是对表面节点进行较小的调整以减小局部应力集中，常用于产品外形需要微调的情况。但无论是尺寸优化还是形状优化往往都无法使结构的性能达到最优，为此人们开始研究拓扑优化。拓扑优化作为最高层次的优化类型，开始于包含指定条件 （例如边界条件和载荷）的初始设计，优化分析过程在符合优化约束 （比如最小体积或者最大位移）的前提下改变初始设计区域的单元密度和刚度，从而确定结构新的材料分布形式。拓扑优化相对于尺寸优化和形状优化而言具有更多的设计自由度，能够获得更广阔的设计空间。拓扑优化能使结构在设计阶段减少设计次数，大大缩短设计时间，使开发和制造的成本得到最大节约。混凝土实体重力坝由于其施工简单、方便取材和良好的耐用性等优点得到广泛应用，但因其体积庞大使得筑坝材料耗费巨大，因而体积的合理优化对降低工程造价具有十分重要意义。

1 拓扑优化的理论方法与应变能优化准则

1.1 拓扑优化的基本理论

结构拓扑优化来源于拓扑学，它以材料分布为优化对象，通过拓扑优化可以在给定的结构设计空间内找出最优的材料分布。Optistruct是一个有限元结构分析和优化软件，用于进行概念设计和精细设计[1-2]。采用Optistruct软件进行拓扑优化，能在提供的优化方法中进行多种响应，比如静态应变能、体积或体积百分比和应力应变等。

1.2 拓扑优化的基本方法

拓扑优化分为离散体结构拓扑优化和连续体结构拓扑优化，后者是结构优化领域中的热点，目前对于连续体拓扑优化方法的研究方法主要有均匀化 方 法 （Homogenization Method）[3]、 变 密 度 法（Variable Density Method）[4]、 渐进结构优化法（Evolutionary Structural Optimization）[5]等。 其中， 均匀化方法和变密度法的研究相对较成熟，变密度法是在均匀化方法的基础上发展起来的，但变密度法相对于均匀化方法来说，具有设计变量少、程序实现简单等优点。

变密度法主要是通过描述材料的分布方式对结构进行优化，变密度法将单元的材料以一种假想的材料密度值作为设计变量，取值为0.0～1.0之间，其中0代表空，1代表实。这样就可以定义一个经验公式来表达密度和弹性模量间假定的函数关系，通过不断调整结构中材料的假想密度值，在目标函数和约束前提下使密度与刚度能较好地匹配设计变量。变密度法通过引入惩罚因子对中间密度值进行惩罚，使密度值向0.0和1.0两边界聚集，最终能使模型更好地逼近实体或空洞。

1.3 应变能准则

为了实现拓扑优化，必须选择收敛快速和计算简便的优化准则，并且该优化准则能全面地考虑优化模型的刚度或者柔度。对于一个安全的结构，其刚度越大，安全性和稳定性就越好。一般可以认为应变能是结构刚度的倒数，通过删减结构中某些未能充分应用的材料，使模型中结构的应变能密度趋于均匀化，结构的总应变能达到最小，即结构刚度最大，此时结构达到最优。

弹性体在受力后要发生变形，同时弹性体内将积蓄能量，这种伴随弹性形变的增减而改变的能量称为应变能。结构的整体总应变能为

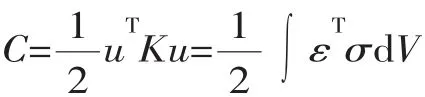
式中，εTσ为微元结构体内存储的应变能密度；V为设计材料总体积。对系统离散，取出单元体分析，则对于平面任意一点应力应变分别为

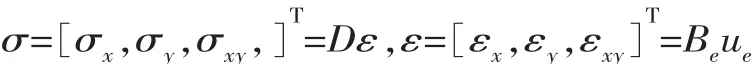
式中，D为弹性矩阵且DT=D；ue为f作用下节点的位移列阵；Be为单元应变矩阵。单元应变能密度为

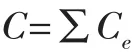
从应变能出发研究结构的性能特性相对于应力、应变等单一指标来说更能够全面的考虑结构中的应力和应变分量，且计算和分析都较方便。可以为整个结构的属性或材料定义应变能，如果应用加权应变能作为优化响应，还可以对整个结构的属性组或材料组定义应变能，能够全面反映不同属性或者不同材料的组合结构的性能指标。

2 工程实例

2.1 工程概况

某实体重力坝，坝高100 m，上游校核洪水位95 m，下游水位10 m。作用荷载有坝体自重，上、下游水压力，上游淤沙压力。泥沙淤积厚度30 m，淤沙内摩擦角14°，浮容重为8 kN/m3；扬压力折减系数0.25，排水孔距上游坝踵10 m；坝体混凝土弹性模量2.5×1010Pa，泊松比0.16，密度2 700 kg/m3；坝基岩体弹性模量2.9×1010Pa，泊松比0.3，密度2 600 kg/m3；混凝土与基岩间的摩擦系数取0.7，用抗剪强度公式计算坝体沿坝基的抗滑稳定安全系数Kf。

2.2 优化思路及步骤

与传统尺寸优化不同，optistruct的拓扑优化是根据模型的有限元分析数据设定响应，按优化目的将响应赋为优化目标、约束、变量三要素，然后由优化模块进行优化。实例的具体拓扑优化步骤如下：

（1）根据坝体资料，应用实体重力坝设计原则设计理论坝体尺寸。

（2）应用CAD软件参数化建立初始模型，包括模型的高和坝底宽度，并将坝体分为拓扑区和非拓扑区。

（3）将模型导入hypermesh进行前处理。施加上下游水位荷载、上游淤沙荷载、自重和扬压力荷载，在此不考虑浪压力、风压力等其他影响小的荷载。

（4）在hypermesh中调出optistruct模块，然后在模块中设置拓扑优化卡片，定义静态应变能、体积百分比、应力为响应，并进行拓扑优化。

（5）从优化后的图形结果中提取出特征点，应用数值拟合方法拟合坝体断面，并对其进行静态分析。

（6）根据拟合坝体的静力分析提取数据，包括最大压应力、上游拉应力、坝体体积及应变能等。

2.3 具体优化步骤

（1）首先根据坝体基本资料，应用实体重力坝设计原则设计理论坝体尺寸。根据SL 319—2005《混凝土重力坝设计规范》，设定坝体上游面为铅直面，坝底宽80 m，坝顶宽10 m，下游坡比m=1:0.78。坝体的断面面积为4 141.03 m2。对断面进行静力分析，得到坝体抗滑稳定性安全系数Kf=1.35，坝踵竖向应力为-0.72 MPa，不存在拉应力，坝趾竖向应力为-1.87 MPa，未超过混凝土抗压应力，表明采用该理论设计符合重力坝设计规范。

（2）建立参数化优化模型，根据坝顶宽度，将距大坝上游面10 m宽度区域定义为非拓扑区，其余为拓扑区，并设定初始坝堤宽76 m。上部是坝体区，下部是地基，地基上下游长度和高度均取坝高。

（3）建立有限元分析模型，并对模型划分网格，根据多次模型试算，发现模型网格尺寸过小，优化时会出现较严重的棋盘现象，而网格尺寸过大，在有限元分析时，得出的应力分析不精确，因此最终划分模型网格单元尺寸定为2 m×2 m的四边形单元格，共9 000个。在模型的自重施加时应说明：应首先在optistruct中的LOAD卡片中设定荷载类型为GRAV，然后添加模型在竖向的重力加速度，重力加速度方向向下取-10 m/s2。

（4）设定优化响应，定义静态应变能最小为优化目标；体积百分比删减率应根据SL 39—2005《混凝土重力坝设计规范》中坝基的抗滑稳定安全系数Kf=f（∑W-U）/∑P反推出坝体的拓扑区的理论删除率应小于62.27%，设定初始删除率为50%；应力约束，在optistruct拓扑优化中只能定义全局应力，定义最大竖向压应力为10 MPa。优化后的拓扑如图1所示。

图1 优化后的拓扑

（5）提取下游面的特征点数据并进行回归拟合，由图1知道，拓扑优化后下游面呈上凸型曲线，所以坝体将按照传统的直线坝形拟合、三次曲线坝形拟合和折线坝型拟合。传统坝形下游直线方程为Y=-0.800 00X+76.000 00 （10≤X≤76）， 其相关系数的平方R2=0.990 00；三次曲线方程为Y=-0.000 17X3+0.01935X2-1.42575X+81.14336 （10≤X≤76）， 其相关系数平方R2=0.99700。折线拟合方程为Y=-0.670 00X+72.820 00 （10≤X≤46）， Y=-1.070 00X+91.220 00（46≤X≤76），其相关系数的平方R2=0.982 00。

（6）对拟合模型进行静力分析，得到 Y方向的应力云图，如图2所示。并提取模型的位移、应力等参数如表1所示。根据SL 319—2005《混泥土重力坝设计规范》规定，用有限元计算的坝基应力，宜小于坝底宽度的0.07，或小于坝踵至帷幕中线的距离，本文取4 m宽处。对于竖向应力，规定：压应力为负值，拉应力为正值。

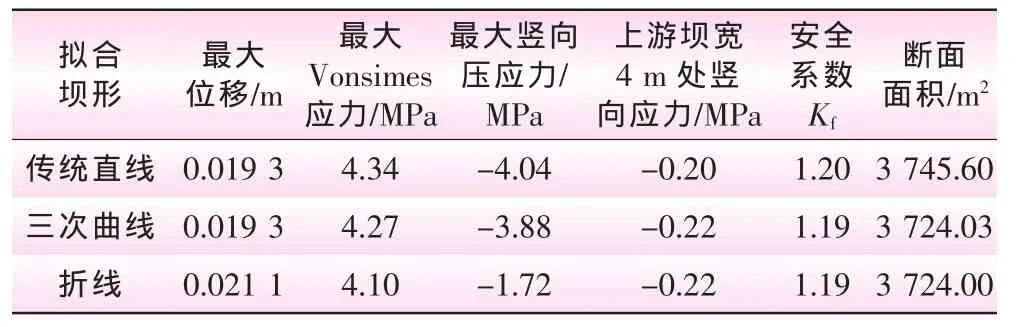
表1 拟合后坝体静力分析数据

2.4 优化结果分析

应变能随迭代次数的变化过程如图3所示，拓扑区体积变化率随迭代次数的变化过程如图4所示。

从表1中可知，对坝体断面进行3种不同的拟合，3种方式的最大Vonsimes应力为均小于混凝土的最大破坏应力；距上游4 m坝宽处的Y方向应力均为负值，并未出现拉应力；坝基抗剪断安全系数Kf均大于规范中的1.1，因此可得该拓扑优化模型均符合规范。3种坝形的断面面积相对于初始断面设计面积减小率分别为9.55%、10.07%、10.07%，可见优化后的坝体断面面积相对于初始断面设计面积来说减小率是非常大的。从表中还可知道，当坝体断面拟合为三次曲线时，位移和竖向压应力均小于传统断面，证明下游坝面拟合为曲面时更有利，但是曲面在施工支模时存在一定困难，因此将下游坝面拟合成折线，发现坝趾处竖向压应力最小，并且各项参数符合规范要求，证明下游坝面拟合为折线是一个较好的优化断面。

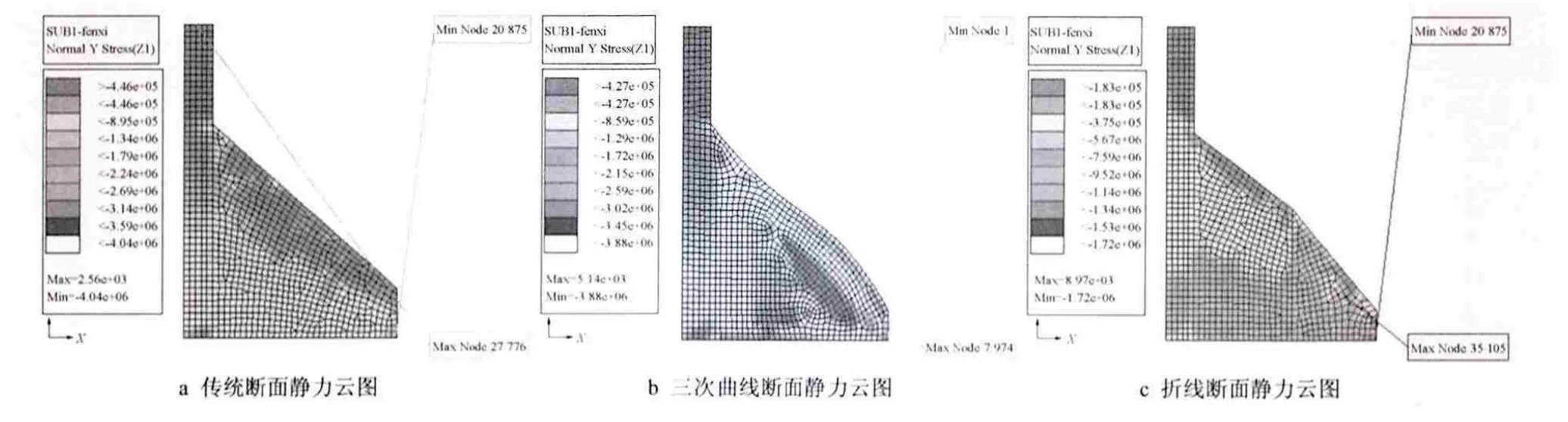
图2 拟合后坝体在Y方向的应力云图

图3 应变能随迭代次数的变化过程

图4 拓扑区体积变化率随迭代次数的变化过程

从图3可知，随着迭代步的不断增加，模型应变能在不断减小，因此坝体的刚度在不断增大，坝体稳定性和应力约束更加满足设定要求。并且从图中可以看出其主要的优化迭代步骤在前几步骤，这是因为optistrcut中通过结构响应的设计敏度分析使迭代解不断逼近优化模型，使结构优化更加快速准确。

从图4可知，模型在优化过程中不断的调整拓扑区的体积百分比，当到第22次迭代步时优化后的体积为全拓扑区的43.31%，即删除率为56.69%，小于62.27%，满足初始设定约束。

3 结 语

本文以Optistruct为平台，采用拓扑优化的变密度法，并结合应变能优化准则对实体重力坝剖面进行了优化分析，结果表明：优化后模型的应力和安全系数等参数均满足规范要求，进一步说明了采用基于Optistruct拓扑优化的方法对实体重力坝的断面进行优化设计是可行的。根据优化后的数据进一步对坝体断面进行传统直线、三次曲线和折线3种不同方式的拟合，发现下游面拟合为折线时，坝址处竖向压应力最小，且参数可满足规范要求。整个优化过程从建模到优化只需要2h左右，大大的缩短了设计周期，节约了设计时间和成本。

［1］张胜兰，郑冬黎，郝琪，等.基于Hyperworks的结构优化设计技术［M］.北京：机械工业出版社，2007.10.

［2］周传月，腾万秀，张俊堂，等.工程有限元与优化分析应用实例教程［M］.北京：科学出版社，2005.

［3］BENDSOE M P,KIJUCHI N.Generating optimal topologies in struc tural design using a homogenization method［J］.Computer Methods in Applied Mechanics and Engineering.1988,71（2）:197-224.

［4］BENDSOE M P.Optimal shape design as a material distribution problem［J］.Structural and Multidisciplinary Optimization.1989,1（4）:193-202.

［5］XIE YM,STEVEN G P.A simple evolutionary procedure for structural optimization［J］.Computers&structures.1993,49（5）:885-896.

［6］SL 319—2005 混凝土重力坝设计规范［S］.

［7］孙素敏，苏志敏，谷俊芹，等.渐进结构拓扑优化在重力坝中的应用研究［J］.科学技术与工程， 2009（11）:164-167.