电控转向系统直流电机实时故障诊断方法*

王 祥，宗长富，邢海涛，吴仁军，张太武，何晨雨

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130025; 2.长安汽车工程研究院，重庆 401120)

前言

汽车电动助力转向(electric power steering，EPS)系统是市场前景非常好的汽车转向系统，直流电机广泛应用在管柱式和小齿轮式EPS产品上。线控转向(steer-by-wire，SBW)系统以其理想的转向特性和主动与被动安全性等优势被认为是最先进的汽车转向系统，但这些优势是建立在系统能够可靠工作的前提下。电控转向系统的故障诊断容错控制应该能够快速准确地指出故障源，并做出相应的容错控制动作，减小甚至消除其对交通环境产生的不利影响。电机作为电控转向系统的动力源，其故障诊断容错控制则是不可或缺的一部分［1-3］。

目前对电机故障诊断的研究主要集中在大型电机设备上，并且需要专用的故障诊断仪。在小功率永磁直流电机研究方面:文献［4］中通过对电枢电流信号的处理实现故障特征提取，结合人工智能方法可实现4种故障识别，这种方法需要数台同型号电机作为故障样本，但仍不能满足汽车故障诊断的高实时性要求;文献［5］和文献［6］中在电机空载状态下分别利用状态观测器和方波脉冲函数法对电机参数进行估计，通过对比有故障和无故障的参数变化实现故障检测。这些故障诊断方法均是对电机具体的故障源进行诊断，如换相片间短路和绕组开焊等。所用故障检测方法须对一段时间序列数据进行处理，实时性稍差。而对于使用直流电机的汽车电控转向系统而言，要求故障检测和诊断具有较高的实时性，方法不能过于复杂，只需诊断出故障元件即可。鉴于此，本文中所研究的电控转向系统直流电机故障诊断方法，旨在电机负载状态前提下，针对电机的突变故障，提高故障检测的实时性与故障诊断精度，简化故障诊断方法，为系统的故障容错控制提供可靠的依据。

1 直流电机参数估计

对电机参数进行实时估计是进行电机故障诊断的核心工作。结合带有遗忘因子的递推最小二乘法和直流电机电压模型，能对工作中电机的电枢电阻和电机常数进行实时估计。

1.1 直流电机模型

直流电机的常用简化数学模型为

式中:L为电枢电感;i为电枢电流;R为电枢电阻;k为电机常数;ω为电机转速;u为电枢端电压;J为电枢转动惯量;C为阻尼系数;f为库仑摩擦力;TL为阻力矩。电机的输入为u和TL，状态变量为i和ω，且模型是非线性的。

可以看出，式(1)是电压平衡方程，式(2)是电机电枢轴上的转矩平衡方程，若要利用该模型对负载状态的电机参数进行估计，须测量电机所有的输入和状态信息，这在汽车电控转向系统中是无法实现的，也是对负载状态下的电机难以进行参数估计的原因。考虑到电控转向系统中，电机的电枢电压和电流是直接测量量，角速度可以由转向盘转角或小齿轮转角换算得到。因此，这里只用式(1)作为对电机参数进行估计的基础模型。

1.2 参数估计方法

用于系统在线参数估计的方法有脉冲函数法、状态滤波法和递推最小二乘法等。递推最小二乘法除了具有简单实用、收敛可靠和几乎无须验前统计知识等优点以外，还无须在计算机中存储和重复计算以往的全部输入、输出数据，减少了计算机的工作量。但随着数据的增长，增益矩阵将逐渐趋于零，以致递推算法逐渐失去修正能力，出现“数据饱和”现象。这种缺陷会导致估计过程中无法快速检测到电机参数的变化，影响故障检测和诊断的实时性［7］。

使用带有遗忘因子的递推最小二乘法作为电控转向系统电机的参数估计方法，其递推公式如下:

式中:x为状态向量;P为估计噪声协方差矩阵;A为状态转移矩阵;λ为遗忘因子;K为参数估计增益。式(3)和式(4)为算法递推初值;式(5)～式(7)为算法递推公式。需要说明的是，为让算法能检测到因电机故障而引起的参数突变，须强调新数据的重要性，减少旧数据对参数估计的影响。所以，在标准的递推最小二乘法基础上引入遗忘因子，它可在0～1间作调整，当λ=1时，式(3)～式(7)即为标准的递推最小二乘法;当λ=0时，算法将对过去的数据没有任何“记忆”，造成估计值的剧烈振荡，不收敛。通常λ的取值范围为0.9～1，使用时应根据被估计参数跟随实际参数的变化情况来确定。

1.3 电机参数估计

为了估计电机参数，须将电机模型与参数估计算法相结合，得到电机参数的估计算法。由于电控转向系统中的电机电感较小，数量级为1mH，故可忽略电机突变故障对电感的影响，即假设电枢电感为定值，L=1mH。

应用中，将式(1)写成:

1.4 参数估计条件

在实际应用中，由于递推最小二乘法须满足持续激励的条件，即当电机电枢电流接近零时，电枢电阻的估计值会不准确甚至发散;同理，当电机转速接近零时，电机常数的估计值也有同样的问题。因此，当电机电流或转速接近零时，将上一时刻的电阻或电机常数估计值作为当前时刻估计值进行下一步迭代。这样，估计器一直处于运行状态，可以在小电流状态下通过估计电机常数进行电机故障诊断;在低转速状态下通过估计电枢电阻进行电机故障诊断。至于电流和转速同时很小状态下的电机故障，因发生机率很小，不予考虑。

2 电机故障诊断方法

2.1 电机故障的模式

电控转向系统中电机的突发故障主要包括:电枢绕组元件开路，由于焊接不良引起绕组与换相片间的断路;匝间短路，由于绕组漆膜划伤或被高压击穿而造成线圈匝间短路;绕组脱焊，由于绕组端头与换相片虚焊造成的两相邻线圈同时与换向片断路。这些故障都会引起电枢电阻和电机常数的突变，导致电机不能按照既定的控制目标运行甚至失控。

2.2 电机故障的检测

如果能对电控转向系统电机的电枢电阻和电机常数进行实时监控，即在线估计电机参数，通过检测估计值与电机正常工作时参数的差值和故障阈值即可及时发现电机故障，为相应的故障补偿提供依据。故障阈值根据实验结果的精度来确定。为简化算法，提高故障诊断的实时性，本文中所述的电控转向系统电机故障诊断方法只通过电机参数的突变来确定电机处于故障状态，而无须指出电机的故障源。

如果电控转向系统电机发生故障，EPS系统一般会减小甚至取消电机的助力，完全依靠驾驶员手力进行转向操作;SBW系统中，会采用灯光或者声音信号提示驾驶员，并采用冗余电机完成故障电机的工作。

3 实车实验及结果分析

为验证上述电控转向系统电机故障诊断方法，进行了实车实验。实验车为在国内某品牌A级车基础上改装而成的线控转向汽车，其线控转向系统的控制和电机故障诊断方法均采用基于Matlab/xPCTarget的快速原型技术实现，图2为实车测控系统。

3.1 基于xPC-Target的快速原型技术

Matlab/xPC-Target是一种用于产品原型开发和测试的PC机解决途径，它采用TCP/IP协议通信的双机模式来提高系统实时计算的能力。使用中，宿主机将建立好的Matlab/Simulink控制模型和电机故障诊断方法编译成可执行文件下载到目标机中，目标机实时运行并通过I/O接口与电机驱动电路和各种传感器进行数据交换。与此同时，可通过宿主机进行信号与变量的监视和实验数据采集。

3.2 电机参数辨识

电控转向系统电机的故障诊断方法须实时计算电机估计参数与参考值的差值，参考值的准确性将直接影响电机故障诊断的阈值。

选取能使参数估计器具有持续激励的转向盘转角单方向匀速输入工况，对线控转向汽车的转向执行电机参数进行3轮辨识，将这3轮辨识结果的均值作为产生故障诊断差值的参考值，结果如表1所示。

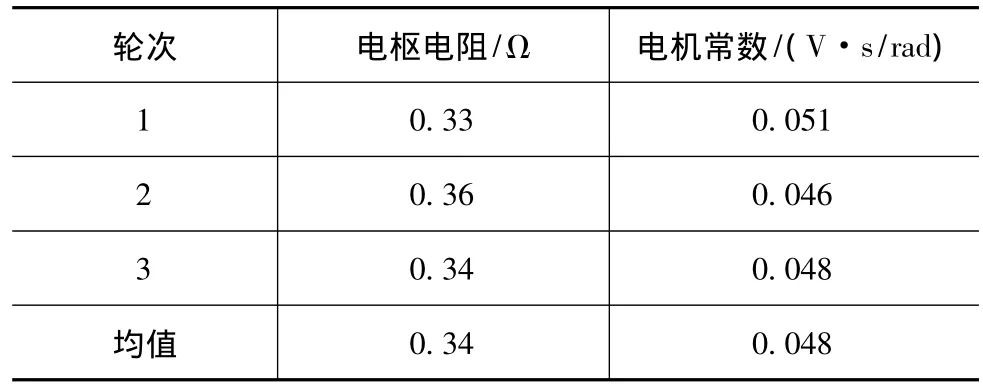
表1 电机参数辨识结果

3.3 电机故障模拟

本文中所针对的各种电机突变故障均因电机内部元件的短路或者断路造成，而实验中很难对工作时的电机人为施加或解除故障。鉴于此，对电机的故障模拟主要通过在电机运行时突然串联大功率铝壳电阻来实现。

需要说明的是，这种故障模拟方式在“改变”电枢电阻的同时，对电机常数没有影响。而电机真实故障时，由于内部线圈连接方式的变化会导致电枢电阻和电机常数同时变化。

3.4 实验结果分析

由于该电机故障诊断方法与车速无关，且从场地限制和实验安全考虑，实验起始车速设定为20km/h，转向盘幅值为47°的正弦输入工况来验证故障诊断方法对电枢电阻突变故障检测的准确性。为便于对比实验结果，SBW系统中转向盘到小齿轮的角传动比设为1。

实验中，8.5s左右在电机回路串联0.7Ω电阻，并在18.5s左右解除故障，实验结果见图3～图7。图3为转向盘与小齿轮转角变化曲线;图4和图5分别为电枢端电压和电枢电流变化曲线。在电机故障期间，由于电枢电阻的突增，电枢端电压达到了电源额定电压，电流无法继续增大而导致小齿轮对转向盘转角的跟随性能下降。如果电阻继续增大，则会导致系统功能进一步下降甚至失效;图6和图7中的实线分别为电枢电阻和电机常数的估计值，虚线为电机故障状态(其中，“0”表示无故障，“1”表示有故障)。由图可见:电机电阻故障施加后，电机参数估计方法可及时准确地检测电机参数(电枢电阻)的变化，并且能够反映参数(电机常数)估计不受故障影响的可靠性。

综合考虑电机参数估计结果、输入信号噪声和估计误差的影响，电枢电阻故障检测阈值(图6中点划线)设为±0.15Ω，即电枢电阻与参考值的差值绝对值超过0.15Ω就认为电机出现故障;电机常数故障检测阈值(图7中点划线)设为±0.015V·s/rad，即电机常数与参考值的差值绝对值超过0.015V·s/rad就认为电机出现故障。在该实验中，从施加电机故障到电机电阻估计值超过故障检测阈值，产生故障诊断结果用时0.08s，而电控转向系统用永磁直流电机的机械时间常数的数量级为0.1s，表明所提出的诊断方法能够在电机故障引起系统失效前诊断出电机故障。需要说明的是，永磁直流电机在实际使用过程中一旦发生故障，电机的电阻和常数一般会同时变化，导致电机的输入电压与电流和转速两个状态发生相应的变化。通过文中的参数估计方法与故障检测阈值，亦可检测出电阻与电机常数同时发生的异常变化，从而确定电机故障。另外，为了使估计参数能及时跟随电机实际参数的变化，满足故障诊断实时性的要求，经反复实验，取电机参数估计方法的遗忘因子为0.98。

4 结论

提出了一种基于具有遗忘因子的递推最小二乘法的电控转向系统直流电机故障诊断方法。首先简化了永磁直流电机的数学模型，将其与参数估计方法结合得到电控转向系统直流电机的参数估计算法。通过对线控转向汽车的转向执行电机在线施加和解除故障，验证了电机参数估计的准确性和实时性。根据实验结果，确定了电机故障检测阈值和参数估计算法的遗忘因子。结果表明:该方法经过实验调试后，可对电控转向系统的直流电机故障做出实时准确的诊断，并且故障检测阈值较小，具有较高的故障诊断精度。

［1］Ryouhei Hayama，Masayasu Higashi，Sadahiro Kawahara.Faulttolerant Automobile Steering Based on Diversity of Steer-by-Wire，Braking and Acceleration［J］.Reliability Engineering ＆ System Safety，2010，95(1):10-17.

［2］刘方，陈慧.TIF助力电动机状态参数估计及故障诊断［C］//2008中国汽车工程学会年会论文集.北京:机械工业出版社，2008:696-699.

［3］宗长富，麦莉，郭学立.汽车前轮电子转向系统［J］.中国机械工程，2004，15(11):1022-1026.

［4］刘曼兰.永磁直流电机故障在线监测与智能诊断的研究［D］.哈尔滨:哈尔滨工业大学电气工程系，2007.

［5］Tutunji Tarek A.DC Motor Identification Using Impulse Response Data［C］.EUROCON2005，Belgrade，November 22-24，2005.

［6］刘向群，杨静，等.基于参数估计和人工神经元网络的永磁直流电机故障检测与诊断［J］.微特电机，1999，27(6):8-12.

［7］Gadda C D，Laws S M，Gerdes J C.Generating Diagnostic Residuals for Steer-by-Wire Vehicles［J］.IEEE Transactions on Control Systems Technology，2007，15(3):529-540.