基于灰色理论ZPW2000A无绝缘轨道电路故障风险分析

马 涛，米根锁，齐 东

(兰州交通大学自动化与电气工程学院，兰州 730070)

基于灰色理论ZPW2000A无绝缘轨道电路故障风险分析

马 涛，米根锁，齐 东

(兰州交通大学自动化与电气工程学院，兰州 730070)

铁路运输系统中各个设备的故障模式存在不同的风险水平，而传统的RCM方法进行风险分析时存在精度不高的问题。在FMEA进行定量风险分析的基础上，再通过灰色关联度方法对FMEA风险分析中的各个决策因素进行加权处理，实现了考虑各因素之间相对权重的故障模式风险分析，提高了分析的准确性。将此方法应用于铁路信号设备，以ZPW2000A无绝缘轨道电路作为实例，通过分析计算表明该方法可行有效，能为改进铁路运输系统各个设备的维修策略提供有力的科学依据。

灰色关联度;故障风险分析;ZPW2000A无绝缘轨道电路;RCM分析;维修策略

我国铁路近年来快速发展，这对保障行车安全的信号设备的可靠性提出了更高的要求。以可靠性为中心的维修(RCM)是目前国际通用的用以优化维修策略为目的，确定设备维修需求的系统工程过程［1］。此方法打破了我国铁路信号设备传统的“定修”模式，克服了以往检修频繁、盲目维修的问题，不仅降低了维修成本和维修人员的劳动强度，使维修体制更具科学性，而且可以显著提高信号设备的可靠性水平。但传统的RCM风险分析方法是通过对设备进行故障模式与影响分析(FMEA)，根据分析结果对故障模式风险进行排序，以此为依据来制定有效的维修策略。但该方法没有考虑(FMEA)分析中各因素间的相对权重等影响因子，存在分析精确度不高的问题，而引入灰色理论中的灰色关联分析方法可以弥补这一不足。因此，本文研究了基于灰色关联度分析的设备故障定量风险分析方法，并应用于铁路信号设备的风险分析中。

1 灰色理论和RCM分析相结合的设备风险分析方法

1.1 传统RCM风险分析方法

传统的RCM定量风险分析方法的核心是进行设备的FMEA分析，确定系统或者设备每个最低组成部分的故障模式，然后来评定每个故障模式的风险等级，再依据风险分析结果针对不同严重程度的故障模式提出设备的维修措施建议，得到改进的维修策略。FMEA最常采用的分析方法是风险优先级法RPN(风险评估评价的尺度)，其基本方法是:确定系统最小组成的子系统单元;描述各单元的功能，并确定各单元的故障模式;确定每一种故障模式的严重度Severity(以下简称为“S”—根据可能出现的人员伤亡、环境损害和任务失败等方面的影响程度确定);发生度Occurrence(以下简称为“O”—故障发生频繁程度的度量);检测度Detection(以下简称为“D”—故障可以被检测到难易程度的度量);最后计算风险优先级指数RPN，它与 S、O、D 三者的关系为

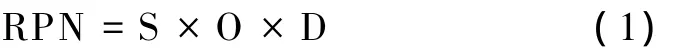
S、O、D三个因素的评分标准如表1所示。RPN数值的大小就代表了故障模式的风险等级大小，由此为依据来改进设备的维修策略，使设备维修更具科学性。FMEA方法的详细介绍详见参考文献［2］。

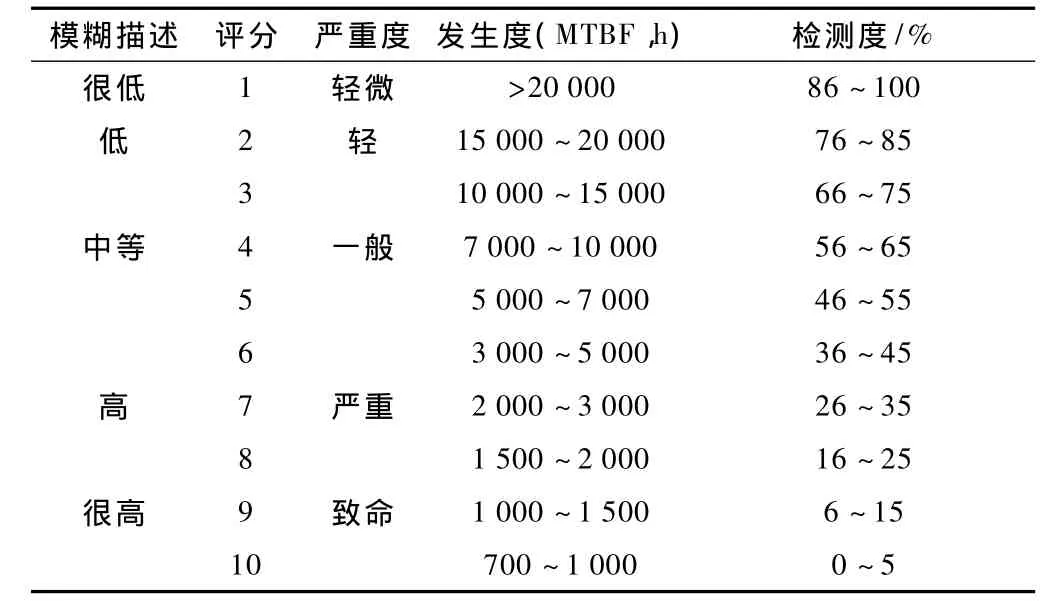
表1 故障风险分析各项指标评分标准

1.2 基于灰色关联度的定量风险分析方法

传统RCM分析方法进行FMEA分析时用RPN值来评价设备各子系统故障模式的风险水平。但RPN数值的计算中没有考虑S、O、D三者之间的相对重要度，将其等同对待，这样会造成不同故障模式的S、O、D定量值的乘积可能产生同样的RPN值，但这些故障模式的风险水平是不同的。因此存在着分析精确度不高的问题。我国学者邓聚龙教授在1982年开创了灰色系统理论［3］，其优势是可以对部分已知的模糊信息进行分析。其中灰色关联度分析法则是以系统内部各因素间相互关系的相似程度来度量其关联程度，因此在FMEA分析的基础上，再运用灰色关联度方法进行故障风险分析［4］，必然能有效提高分析的精度。分析方法的基本流程如图1所示［5］。

图1 灰色关联度分析流程

具体步骤为:首先通过FMEA分析确定系统组成单元所有可能的故障模式，并对各个故障模式的决策因素S、O、D进行模糊评价。模糊评价的描述:“很低”、“低”、“中等”、“高”和“很高”共 5级，评价方法见表1所示［5］。接着模糊评价进行反模糊化。模糊集的脆性系数K(x)为

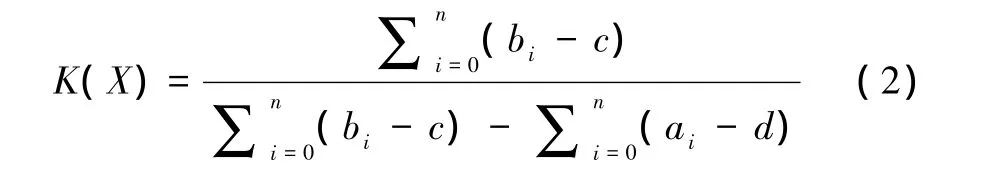
对应各模糊评价的隶属函数如图2所示［6］，从图中可得到式(2)中相关参数的值。以模糊评价描述“低”为例，在取其脆性系数时，可由图2得a0=2，b0=5，a1=b1=3.5，c=0，d=10，代入式(2)有

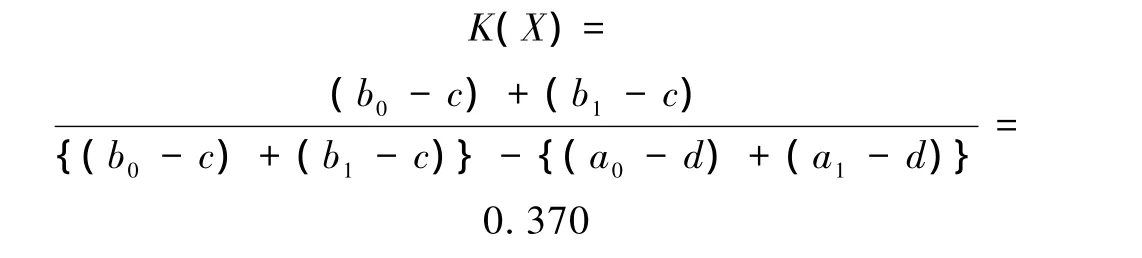
图2 隶属函数图

同理可得其他模糊语义描述所对应的脆性系数，“很低”为 0.196，“中等”为 0.583，“高”为 0.804，“很高”为0.952，如表2所示。

表2 模糊语义反模糊化脆性系数

根据得到的脆性系数以式(3)的形式表示的比较序列

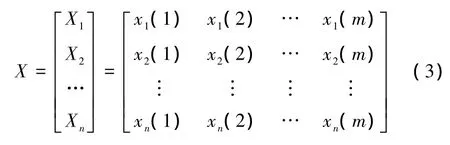
式中，X1，X2，…，Xn表示 n个故障模式对应的比较序列;{xi(1)，xi(2)，…，xi(m)}表示第 i个故障模式的m个决策因素模糊语义评价对应的脆性系数。

同时得到反映所有决策因素的理想期望水平的标准序列，即

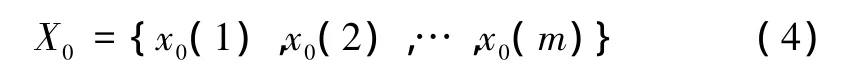
由此，计算比较序列和标准序列的差序列

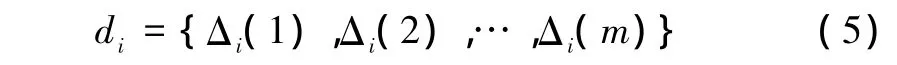
式中Δi(k)=xi(k)-x0(k)，则灰色关联度系数可由式(6)求得

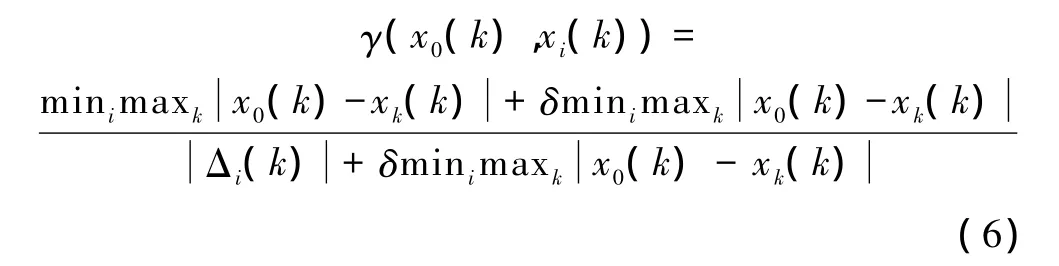
式中，x0(k)表示标准序列中第k个决策因素对应值;xi(k)表示比较序列矩阵中第i个故障模式第k个决策因素对应值;δ为分辨系数，δ∈(0，1)，它仅影响相对风险值，因此通常可取 0.5［6］。

计算两序列(比较序列与标准序列)的关联度，可由式(7)得到

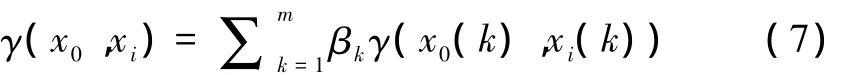
式中，βk为决策各因素的权重系数，且满足=1。βk可用层次分析法(AHP)得到，层次分析法的详细步骤详见参考文献［7］。

由此便可得到故障模式的灰色关联度值，它反映了某一故障模式和决策因素之间相关联程度的关系，关联度越大的故障模式的整体影响越小，则该部件的风险优先等级越低。根据得到的灰色关联度值就可进行系统各个故障模式的风险等级排序，完成设备故障风险分析。

2 实例分析

ZPW2000A无绝缘轨道电路是我国铁路应用最广泛的信号设备之一，其安全性和可靠性关乎列车运行安全。因此，本文以ZPW2000A无绝缘轨道电路为研究对象进行定量风险分析。根据RCM分析方法中系统划分原则，可将本体系统划分为发送系统、接收系统、冗余衰耗系统、防雷系统、扼流匹配变压器、调谐匹配单元、补偿电容、空心线圈、机械绝缘节空心线圈、SPT电缆、通信接口板、扼流变压器、信号传输线、条件线和监测线共15个子系统，各子系统又包括若干部件。由于对各个子系统的分析方法完全相同，这里仅对发送系统和接收系统进行分析验证。具体分析计算步骤如下。

(1)通过ZPW2000A无绝缘轨道电路发送器和接收器运行、维修的历史记录进行统计分析，并采用专家调查法，可得到系统RCM分析结果，如表3所示［8］。

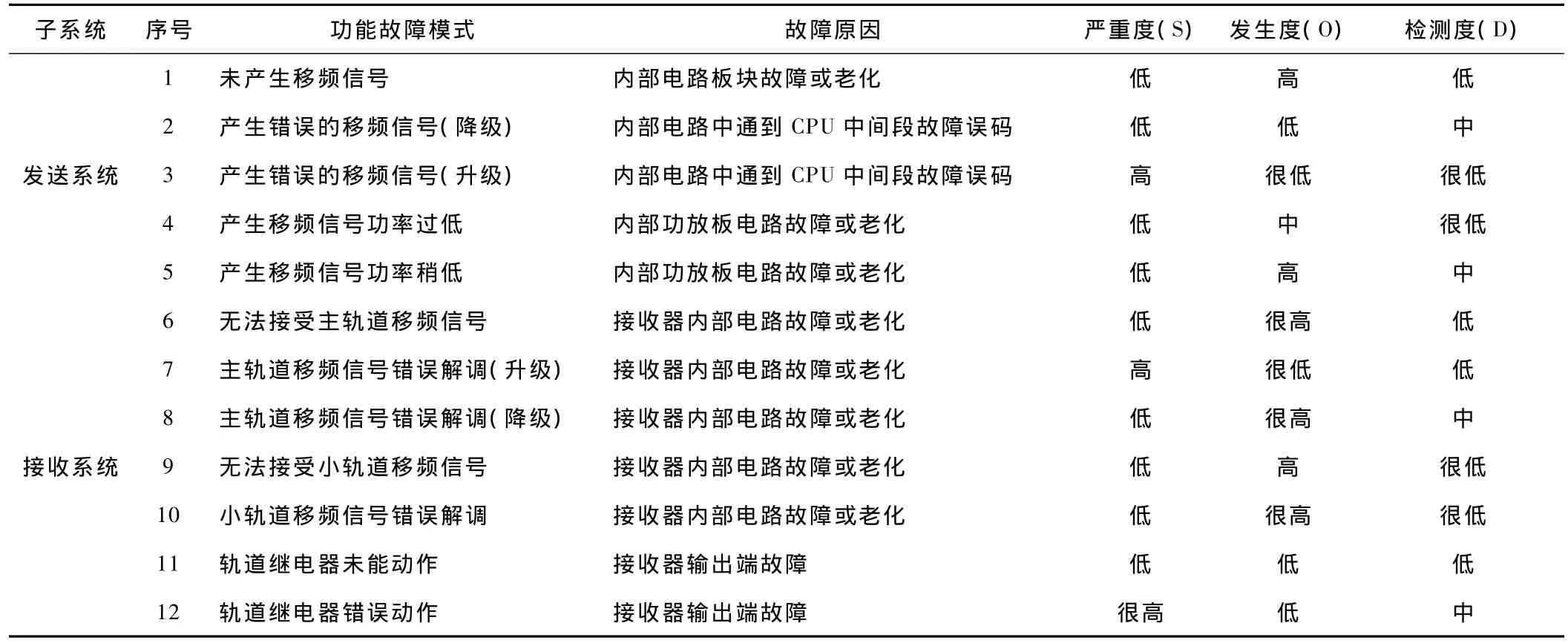
表3 ZPW2000A无绝缘轨道电路发送接收系统RCM分析结果

(2)对各决策因素反模糊化，得到比较序列矩阵

(3)取各决策因素最低模糊语义评价的反模糊化值来确定标准序列。若取标准序列为零矩阵，则两序列(比较序列与标准序列)的差序列仍为比较序列。式(6)便可简化为

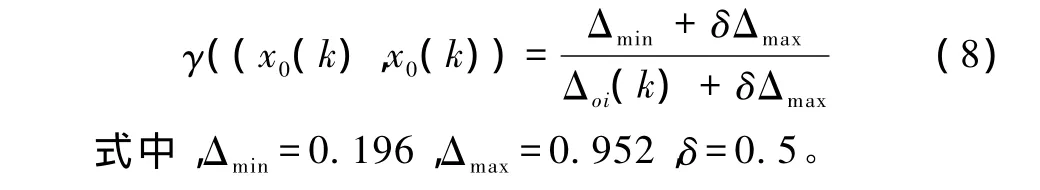
由式(8)便可得到每个故障模式的决策因素相对应的灰色关联度系数(γs、γo、γd)。

(4)通过咨询信号厂家和铁路局专家以及现场运行、维修人员，参照设备设计说明和历史维护数据，利用AHP法得到式(7)的各因素(故障影响严重度S、发生度O和检测度 D)的权重分别为0.5、0.25和0.25。

(5)由式(7)代入对应的灰色关联度系数可得各故障模式所对应的灰色关联度，同时再根据表1的标准按式(1)计算各故障模式的RPN值，并对两种方法的计算结果分别进行故障模式的风险排序，排序结果如表4所示。

由表4可见:两种方法的结果对比可看出排序的基本一致性。而灰色关联度故障风险分析方法由于考虑了各因素间的相互权重，克服了不同S、D、O值得到相同RPN值的不足，比传统RCM风险分析方法提高了分析精度。而且可以看出，RPN排序的风险等级分为9级，而灰色关联度排序的风险等级为12级，灰色关联的分级更为精确详细。各个系统的故障模式风险优先级排序也和现场运行、维修情况比对一致。

表4 ZPW2000A无绝缘轨道电路接收和发送系统故障风险分析结果

4 结语

利用灰色理论进行铁路信号设备的故障风险分析，可避免传统RCM分析方法没有考虑同一故障模式各因素之间的相对重要度而产生的误差，有效提高了分析精度。将该方法应用于ZPW2000A无绝缘轨道电路设备的故障风险分析，用以确定设备各个子系统的故障风险等级，为制定科学有效的维修策略提供了有力的科学依据。该方法可作为一个通用方法，应用于我国铁路信号系统其他设备的故障风险分析中。

［1］ Moubray J.以可靠性为中心的维修［M］.北京:机械工业出版社，1995:6-8.

［2］ Stamatis DH.Failure mode and effect analysis-FMEA from theory to execution［M］.New York:ASQC Press，1995:63-67.

［3］ Deng J.Control problems of grey systems［J］.Systems Control Letters，1982，1(5):288-294.

［4］ Ben-Daya M，Raouf A.A revised failure mode and effects analysis model［J］.International Journal of Quality Reliability Management，1993，3(1):43-47.

［5］ Chang C L，Wei C C，Lee YH.Failure mode and effects analysis using fuzzy method and grey method［J］.Kybernetes，1999，28(9):1072-1080.

［6］ Chen C B，Klien CM.A simple approach to ranking a group of aggregated fuzzy utilities［J］.IEEE Trans Syst Man Cybernet，Part BL:Cybernet，1997，27(1):26-35.

［7］ Anand Pillay，Jin Wang.Modified failure mode and effects analysis using approximate reasoning［J］.Reliability Engineering and System Safety，2003，79(1):69-85.

［8］ 李文海.ZPW-2000A移频自动闭塞系统原理、维护和故障处理［M］.北京:中国铁道出版社，2010:57-66.

Fault Risk Analysis on ZPW2000A Uninsulated Track Circuit Based on Gray Theory

MA Tao，MI Gen-suo，QI Dong
(School of Automation and Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

The fault models of all the equipments in railway transport system have different risk levels，but the traditional RCM method of risk analysis has some problems in precision.In this method proposed by this paper，every decisive factor in the process of FMEA risk analysis is weighted based on the FMEA quantitative risk analysis by using gray correlation method，so that the fault model risk analysis considering the relative weights of various factors can be achieved，therefore the accuracy of the analysis can be improved.This method can be used in the railway signal equipment， and in this paper，ZPW2000A uninsulated track circuit are taken as an example for risk analysis.Then the analysis and calculation results show that:this method is a feasible and effective method，and it can provide a strong scientific basis for the improvement of the maintenance strategies of various equipments in railway traffic system.

gray correlation degree;fault risk analysis;ZPW2000A uninsulated track circuit;RCM analysis;maintenance strategy

U283.2

A

1004-2954(2013)04-0115-04

2012-08-15

马 涛(1986—)，男，硕士研究生，E-mail:283584996@qq.com。