基于排队论的地面防空系统服务概率研究

2013-09-02朱雪平李东伟王敬华

指挥控制与仿真 2013年1期

朱雪平，李东伟，王敬华

(防空兵学院，河南郑州 450052)

在研究地面防空系统作战效能、地面防空作战部署方案优化和地面防空作战资源需求等问题时，都必然涉及地面防空系统的服务(可射击)概率问题。若采用解析算法计算地面防空系统的服务(可射击)概率，排队理论是人们通常选择的方法。排队理论(Queuing Theory)也称随机服务系统理论，是运筹学的重要内容，同时也是研究服务系统服务效率和服务系统最优化的有效工具。20世纪初，丹麦数学家、电气工程师A.K.Erlang把概率论方法应用于解决电话交换机呼叫问题，从而开创了这门应用数学学科。20世纪30年代中期，W.Feller引进了生灭过程，排队论作为一门重要的学科才被数学界承认。20世纪50年代初，D.G.Kendall对排队论进行了系统的研究，应用嵌入马尔可夫(A.Markov)链方法研究排队论，使排队论得到了进一步的发展。

运用排队理论计算地面防空系统的服务(可射击)概率时，受抽象为随机服务系统的简化过程及计算模型自身的制约，可能使地面防空系统的服务(可射击)概率计算结果大于实际结果。因此，将给防空兵指挥员和指挥机关一个过于乐观的预期，影响指挥决策的准确性。因此，本文就采用排队理论解算防空系统的服务(可射击)概率的误差问题进行讨论。

1 地面防空系统服务(可射击)概率问题的一般描述

地面防空系统服务(可射击)概率，指一次战斗中地面防空系统平均射击的空袭兵器数量与来袭空袭兵器总数的比值。地面防空系统服务(可射击)概率是评估地面防空系统作战效能的重要指标，系统服务(可射击)概率的取值直接制约地面防空系统的作战效能，其值取决于空袭兵器的进袭强度、进袭条件和地面防空武器系统的战术等。

若应用排队论求解地面防空系统服务(可射击)概率，必须将地面防空系统抽象为随机服务系统。通常假定地面防空系统由同一型号防空武器系统构成，组成拒绝等待系统(低空近程防空武器系统)或有限等待系统(中高空中远程防空武器系统)，抗击以某种规律进入的空袭兵器的攻击。

2 排队论模型计算服务概率的误差分析

2.1 非对抗性误差

排队论模型为非对抗性模型。因此，运用排队理论解决地面防空系统服务概率有其先天不足的源由。

地空对抗是激烈的对抗活动，空袭方为达成空袭作战目标，必须首先对地面防空系统实施压制。按照美军的空袭作战要则［1］:在空袭作战编队中约有25%～40%的力量用于压制对方的地面防空力量。根据空军某研究所张学成总工搜集统计提供的资料［2］:在抗美援朝战争中，我志愿军所属高炮部队日战损率最高时达1.8%，整体战损率为7%，被攻击战损率为13%;在援越抗美战争中，我高炮部队的整体战损率为4%，被攻击战损率为17%。第四次中东战争中，以色列参战防空力量的整体战损率为20%，日战损率为1.1%;埃及参战防空力量的整体战损率为44%，日战损率为2.4%;叙利亚参战防空力量的整体战损率为25%，日战损率为1.4%。根据以上资料可知，在一次战役(战斗)中，地面防空系统被空袭兵器攻击的战损率大于10%。因此，构成地面防空系统的射击单元(服务台数)数量随战斗进程不断减少，而非固定不变的。

通过以上分析，可知:由于排队论模型的非对抗性，将导致构成地面防空系统的射击单元(服务台数)产生大于10%的误差，引起所计算的地面防空系统的服务(可射击)概率产生误差。

2.2 忽略空袭兵器空间分布的误差

排队论模型以假定空袭兵器流在时间上的分布为基础展开讨论。判定地面防空系统对空袭兵器的服务(实施射击)条件是:空袭兵器的间隔时间大于地面防空系统的服务时间。排队论模型不考虑空袭兵器的空间分布(进袭条件)对地面防空系统的服务(可射击)概率的影响，如空袭兵器进袭高度和进袭的航路投影捷径等。实际上地面防空系统对空袭兵器的可射击与否与空袭兵器的进袭高度和航路投影捷径密切相关。

1)空袭兵器进袭高度的影响

地面防空系统由于受其可射击高度的制约，并不能对进入系统的全部空袭兵器实施射击。通常情况下，空袭方根据战术要求，空袭兵器将从不同高度实施攻击。蒋为民在《俄罗斯防空体系研究》一书中认为［3］:空袭兵器从高空实施攻击的可能性约为10%，从中空实施攻击的可能性约为20%，从低空超低空实施攻击的可能性约为70%。美军认为［2］:地面防空系统的全部武器，应能对低空超低空实施攻击的空袭兵器进行射击，其中25%的防空武器应能对中高空实施攻击的空袭兵器进行射击。从另一个侧面表明了从中高空实施攻击的空袭兵器约占空袭兵器重量的25%。也说明了美俄两个军事强国对空袭兵器在高度上分布的观点是基本一致的。因此，如果地面防空系统由低空/超低空防空武器构成，则对于进入防空系统的空袭兵器应该有25%～30%是不能实施抗击的。在极端的情况下，由于空袭兵器进袭高度的影响，将会导致计算结果产生25%～30%的误差。

2)空袭兵器进袭航路投影捷径的影响

地面防空武器系统受武器系统有效射程和必需的射击时间的制约，有一个有效拦截半径。比如ADKXX防空武器系统，其有效拦截半径为6km。如果空袭兵器进袭的航路投影捷径大于6km，则该防空武器系统不能对空袭兵器实施有效抗击，即不构成可射击条件。排队论模型并不能考虑空袭兵器进袭的航路投影捷径对地面防空系统可射击概率的影响，认为:只要系统内的空袭兵器在时间上满足可射击要求，即可计入可射击范畴。因此，航路投影捷径也将导致计算的地面防空系统可射击概率值大于实际结果。

空袭兵器进袭航路投影捷径对地面防空系统可射击概率的影响，取决于地面防空系统的战斗部署、防空武器系统的有效拦截半径和空袭兵器的进袭方式等。空袭兵器进袭高度和进袭航路投影捷径的制约，都将导致应用排队论模型计算的地面防空系统的服务(可射击)概率偏大。

2.3 求取稳态解的误差

排队论模型通过建立柯尔莫哥洛夫微分方程组求解地面防空系统服务(可射击)概率。由于求解柯尔莫哥洛夫微分方程组的瞬时解比较困难，因此，将柯尔莫哥洛夫微分方程组变换为代数方程组后实现数值解。即排队论模型最后给出的数值解是地面防空系统达到稳定状态条件下的结果。至于地面防空系统何时达到稳定状态，国内在这方面的研究成果较少。俄罗斯朱可夫防空军事指挥学院(现名为俄罗斯空天防御军事学院)编著的《防空作战模拟与效能评估》［4］一书中指出:在单通道随机服务系统中，瞬态过程在经过2～4倍的平均服务时间会减弱，之后系统内出现稳定状态。随着系统中通道数的增加，瞬态过程会缩短，即系统稳定状态会提前出现。因此，在实际计算中通常认为:当系统的持续时间超过3倍平均服务时间，可以利用稳定状态的计算模型计算地面防空系统的服务(可射击)概率。但由于防空作战的特殊性和战斗持续时间的短促性，其实很难使地面防空系统达到真正的稳定状态。从而导致计算误差。

3 排队论模型与作战仿真方法计算结果的对比分析

3.1 条件设置

防空兵群由3个xx高炮营编成(服务台数m=9)，掩护x炮兵群战役实施过程中的对空安全，3个营间隔xxkm成等边三角形配置，基本火力单位对一个目标的平均服务时间t为45s。假定作战对象以战斗轰炸机实施攻击，空袭兵器进袭强度λ为x批/min，进袭方向服从主攻方向上的截尾正态分布，进袭速度在(200，400)区间内服从均匀分布，进袭高度是服从瑞利分布的随机变量，其分布密度计算模型为

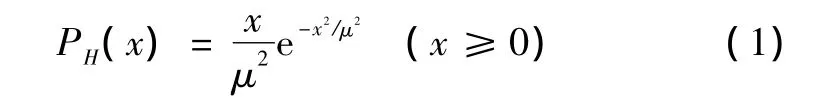
其中，μ依赖于战斗轰炸机所处的进入、攻击、退出状态，参照战场统计资料取值为2000m;航路投影捷径dj是服从负指数分布的随机变量，其分布密度计算模型为

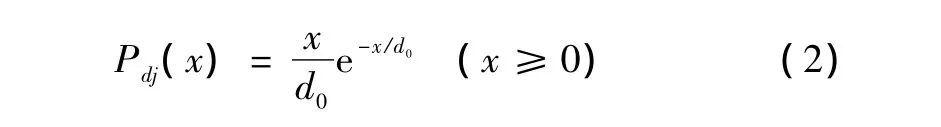
其中，d0依赖于高炮的类型，根据经验与统计资料取值为1500m;作战时间30min。

3.2 计算结果

xx高炮为小口径高炮，故按拒绝等待系统处理，可射击概率计算模型为

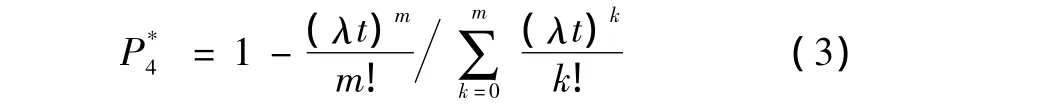
作战仿真采用防空兵指挥学院研发的防空兵作战指挥辅助决策系统提供的防空作战仿真软件计算，计算结果见表1。

表1 防空兵群可射击概率计算结果

3.3 结果分析

从计算结果看，依据排队理论计算结果和作战仿真计算结果差别非常大。排队理论计算结果，由于空袭强度数值小于服务台数目，所以可射击概率均在90%以上，而作战仿真计算结果仅为30%左右。究其原因有4个:1)系统发现目标概率约在90%左右，没有发现的目标系统不能实施服务而产生误差;2)防空兵群由小高炮武器系统构成，进袭目标高度大于XXXXm的比例约等于30%，防空兵群不能实施抗击而产生误差;3)防空兵群采用前三角部署样式，空袭兵器主攻方向上只有一个营(三个服务台)，其它两个营(六个服务台)在主攻方向两侧，根据模型计算，目标航路投影捷径大于武器系统有效抗击航路投影捷径的约为35%，由于防空兵群不能实施有效抗击而产生误差;4)防空兵武器系统的战损率影响了防空兵群的可射击概率。误差分析结果见表2。

4 结束语

地面防空系统的服务(可射击)概率问题，是分析地面防空系统作战效能、地面防空作战部署方案优化和地面防空作战资源需求等相关问题时，必须涉及和解决的一个重要参数。采用解析法计算时，由于排队论模型的局限性，将导致计算的地面防空系统的服务(可射击)概率产生较大误差。为此，应根据地面防空系统的主要特征，对模型计算结果进行合理修正，否则不利于防空兵指挥员和指挥机关正确定下战斗决心。在可能的情况下，应采用作战仿真的方法求取地面防空系统的服务(可射击)概率。