掺Gd3+钼酸盐AMoO4(A=Ca,Sr,Ba,Pb)自旋哈密顿参量的理论计算*

杨维清1)2)† 张胤1) 高敏1) 林媛1)‡ 赵小云2)

1)(电子科技大学电子薄膜与集成电路国家重点实验室,成都 610054)

2)(成都信息工程学院光电技术系,成都 610225)

1 引言

掺稀土离子的钼酸盐可用于激光和发光(包括上转换和下转换发光)器件而受到人们的极大关注[1−6],因此它们的谱学性质就引起了人们广泛的兴趣[7−15].由于掺Gd3+晶体的电子顺磁共振(EPR)谱可在室温下测量,钼酸盐AMoO4(A=Ca,Sr,Ba,Pb):Gd3+的EPR谱就早已被测量[12−15],人们从中得到了它们的自旋哈密顿参量(g因子g//,g⊥和零场分裂).时至今日,这些自旋哈密顿参量并未获得合理的理论解释.原因是:作为S(8S)态离子的Gd3+缺少轨道角动量,故它在晶体中的零场分裂的微观机制非常复杂.除了传统的单电子晶体场机制外,还有相对论晶体场机制,相关(如自旋相关)晶体场机制和二次(quadratic)晶场机制等[16−21].由于这些机制的相对重要性难以决定,以及各机制本身计算的复杂性,长期以来,大量晶体中Gd3+的自旋哈密顿参量都缺少理论解释.鉴于除单电子晶体场机制外的其他机制的作用会部分抵消,我们发展了一种基于单电子晶体场机制的对角化能量矩阵方法来统一计算晶体中Gd3+的g因子和零场分裂,并获得了与实验一致的结果[22−24].本文用该方法计算了AMoO4:Gd3+的自旋哈密顿参量,并对结果进行了讨论.

2 计算

钼酸盐AMoO4(A=Ca,Sr,Ba,Pb)属白钨矿结构,空间群为I41/a[8,25,26].A离子在其中位于四角(S4)对称的八配位位置.Gd3+是4f7离子,自由态Gd3+的基项(或基多重态)为8S7/2.当Gd3+进入AMoO4晶体占据A位置时,其基多重态8S7/2就会被四角晶体场分裂成4个Kramers双重态,它们的J值各为±1/2,±3/2,±5/2,±7/2.在电子顺磁共振谱实验中,外磁场B又会将这些双重态进一步分裂成8个单重态.即±J的简并被解除.4f7离子在四角对称晶场中的EPR谱可用下述有效自旋哈密顿参量Hs描述,即

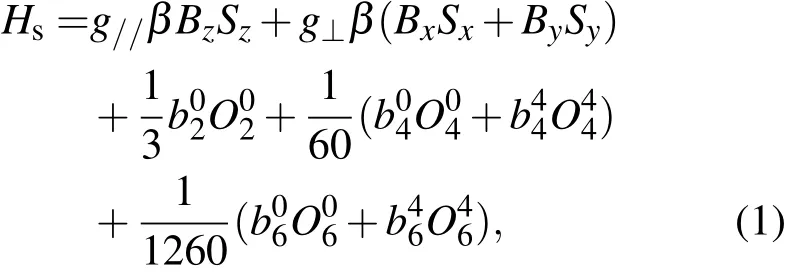
其中β是玻尔磁子,Si为自旋角动量,是自旋算符,式中的自旋哈密顿参量g//,g⊥和可由实验测得的EPR跃迁∆Ei的角度相关获得.据二阶微扰计算,可得这些自旋哈密顿参量与∆Ei)的角度关系[22−24,27].

当外磁场B平行于z(即C4)轴时,EPR跃迁∆Ei(//)为

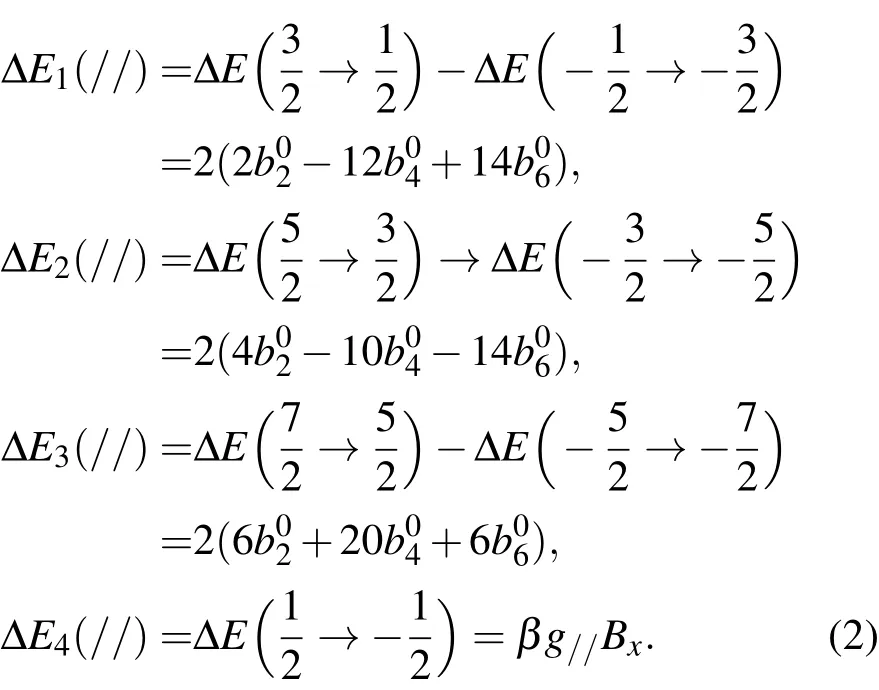
而当外磁场B垂直于z轴并平行于x轴,EPR跃迁Ej(⊥)为

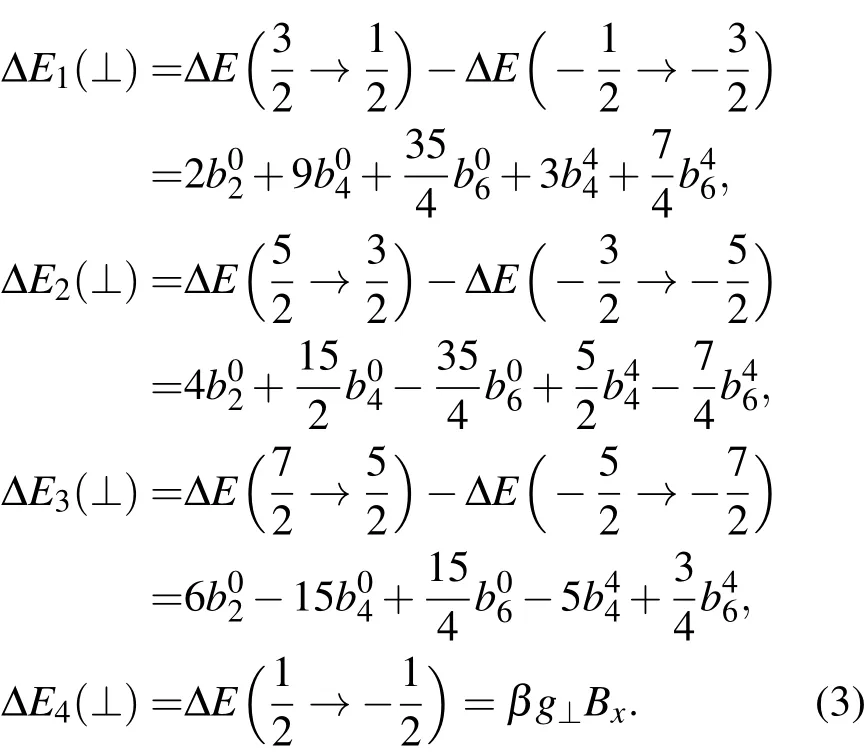
这样,知道了由基项8S7/2分裂成的8个单重态的能级,就能据上述公式计算自旋哈密顿参量g//,g⊥和.

如前所述,4f7离子的基项8S7/2是在四角晶体场和外磁场中分裂成8个单重态的.此时,4f7离子在单电子晶体场机制上的哈密顿量为

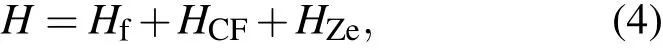
上式中,Hf是自由离子项,HCF是晶体场相互作用项,HZe为磁(或Zeeman)相互作用项.它们可以表示为[28−30]

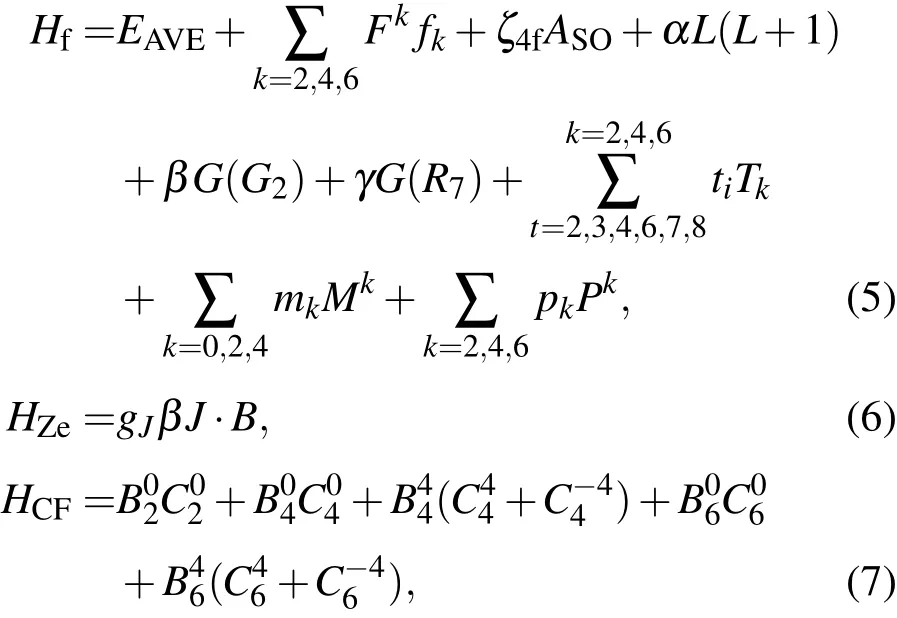
严格地讲,基多重态8S7/2的分裂是它经由上述哈密顿量和其他所有激发多重态相互作用引起,因此应建立对应上述哈密顿量的完全能量矩阵.对4f7离子,这个完全能量矩阵达3432×3432维.这个矩阵实在是太大了,会造成对角化,此能量矩阵的计算量很大.但实际上,4fn离子基多重态的分裂主要决定于与之较接近的低激发态[31].对4fn离子,则主要为与基多重态8S7/2具有相同角动量J(=7/2)的低激发态6L7/2(L=P,D,F,G,H,I)相互作用有关[17,19,32,33].作为一种合理的近似,我们用不可约张量算符构建了包含基多重态8S7/2和激发多重态6L7/2的对应上述哈密顿(即(4)式)的56×56维能量矩阵.对角化此能量矩阵,我们就能得到基多重态8S7/2分裂成的8个单重态的能级,再据(2)和(3)式,我们就可计算4f7离子系统的自旋哈密顿参量.

由于稀土离子在自由状态时,其4fn组态内的各能级间的量子跃迁是宇称禁戒的,不能通过光谱求得这些能级及(5)式中的各自由离子参量.因此4fn离子的自由离子参量常由晶体中的4fn离子的光谱获得[28,30].由于各晶体中4fn离子基团的共价性等性质不一样,这样获得的4fn离子的自由离子参量就有小的差别.在上述能量矩阵中,我们取Gd3+的自由离子参量为文献[28]给出的平均值,它们被列于表1.能量矩阵中的晶体场参量的微观起源很复杂[26,28],因此人们常采用经验的重叠模型[18,20]来计算晶体场参量.对本文研究的AMoO4:Gd3+系统,据重叠模型,晶体场参量可表示为

此处tk(k=2,4,6)是幂指数,对晶体中的4fn离子,可以取t2≈5,t4≈6和t6≈10[34,35].(R0)是内禀参量,其中R0为参考距,可以取被研究的4fn离子系统的金属及配体的离子半径之和.故对AMoO4:Gd3+晶体,我们取R0≈rGd3++rO2−≈2.47Å[36].在AMoO4晶体中,环绕A2+的8个O2−可分成两组,每组中四个O2−的结构数据(金属-配体距)和θi(和C4轴的夹角)是相同的,在第一组中四个O2−的方位角φj(j=1—4)为 φ1+(j−1)π/2,而在第二组中,方位角 φj(j=5—8)为φ5+(j−5)π/2.AMoO4晶体的结构数据,θi和φi列于表2.由于Gd3+的半径ri不同于它所替代的基质晶体中的A2+的半径rh,故Gd3+杂质基团的金属-配体距Ri会不同于基质晶体中对应的距离.我们可用一个近似公式来合理估算杂质中心的金属-配体距R.据文献[36]给出的各种离子在8配位时的离子半径,可以求得AMoO4:Gd3+晶体中各Gd3+杂质中的金属-配体距Ri,它们也被列于表2中.这样,在上述56×56维能量矩阵中,我们就只剩下三个未知参量(R0)(k=2,4,6),它们被视作可调参量,可用对角化能量矩阵方法计算的自旋哈密顿参量来拟合实验值获得.在计算中我们发现:当(R0)取表3中的数值时,计算的AMoO4:Gd3+的自旋哈密顿参量与实验值符合甚好.这些计算值与实验值的对比示于表4.

表1 Gd3+的自由离子参量[28]

表2 AMoO4(A=Ca,Sr,Ba,Pb):Gd3+的结构数据

表3 Gd3+在AMoO4(A=Ca,Sr,Ba,Pb)和某些三价稀土离子在CaWO4中的内禀参量k(R0)(k=2,4,6)(括号中数值为误差)

表3 Gd3+在AMoO4(A=Ca,Sr,Ba,Pb)和某些三价稀土离子在CaWO4中的内禀参量k(R0)(k=2,4,6)(括号中数值为误差)

?

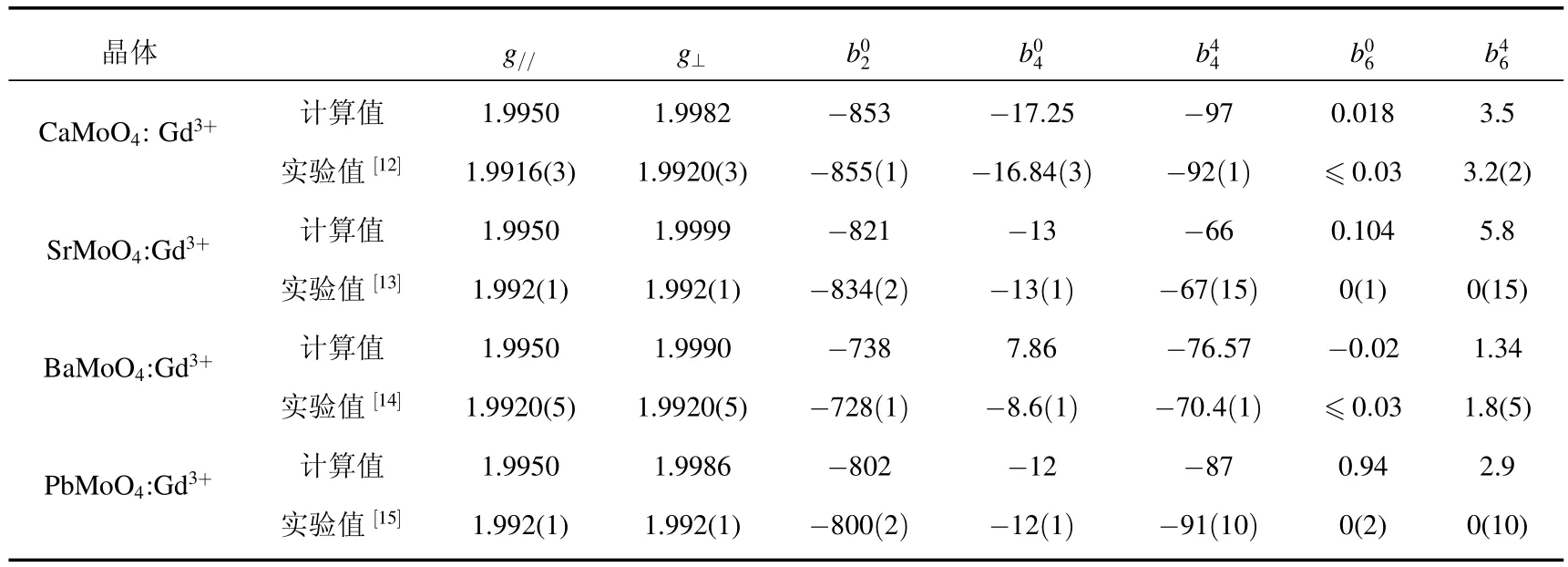
表4 Gd3+在AMoO4(A=Ca,Sr,Ba,Pb)的自旋哈密顿参量g//,g−和bnm(bnm单位为10−4cm−1)(括号中数值为误差)

3 讨论

4 结论

采用基于单电子晶体场机理的对角化能量矩阵方法(矩阵中的晶体场参量采用重叠模型计算),通过调节重叠模型中的内禀参量和,所计算的Gd3+在钼酸盐AMoO4(A=Ca,Sr,Ba,Pb)晶体中的自旋哈密顿参量(g因子g//,g⊥和零场分裂与实验值符合较好.计算结果表明,采用基于单电子晶体场机理的对角化能量矩阵方法,可以合理地计算或解释Gd3+在晶体中四角晶位的七个自旋哈密顿参量.

[1]Han Y F,Li J Z,Chen Z Q,Lin L,Li B,Wang G F 2009 J.Synth.Cryst.38 190(in Chinese)[韩永飞,李景照,陈振强,林浪,李兵,王国富2009人工晶体学报38 190]

[2]Chung J H,Ryu J H,Eun J W,Lee J H,Lee S Y,Heo T H,Chol B G,Shim K B 2012 J.Alloys Comp.522 30

[3]Cao X Q,Wei T,Chen Y H,Yin M,Guo C X,Zhang W P 2011 J.Rare Earths 29 1029

[4]Tang H X,Lü S C 2011 Acta Phys.Sin.60 037805(in Chinese)[唐红霞,吕树臣2011物理学报60 037805]

[5]Sun J Y,Cao C,Du H Y 2011 Acta Phys.Sin.60 127801(in Chinese)[孙家跃,曹纯,杜海燕2011物理学报60 127801]

[6]Yang W Q,Liu H G,Liu G K,Lin Y,Gao M,Zhao X Y,Zheng W C,Chen Y,Xu J,Li L Z 2012 Acta Mater.60 5399

[7]Gavalli E,Angiuli F,Boutinaud P,Mahiou R 2012 J.Solid State Chem.185 136

[8]Trabelsi I,Dammak M,Maalej R,Kammoun M 2011 Physica B 406 315

[9]Wishwamittar,Puri S P 1974 J.Chem.Phys.61 3720

[10]Kurkin I N,Tsvetkov E A 1970 Sov.Phys.Solid State 11 3027

[11]Rosa J,Asatryan H R,Nikl M 1996 Phys.Status Solidi A 158 573

[12]Meilman M L,Slovev N V 1965 Sov.Phys.Solid State 7 2512

[13]Kurkin I N,Stepanov V G 1965 Sov.Phys.Solid State 7 223

[14]Meilman M L,Samoilovich M I,Potkin L I,Sergeeva N I 1967 Sov.Phys.Solid State 8 1864

[15]Kurkin T N,Shekun L Y 1965 Sov.Phys.Solid State 6 1560

[16]Newman D J,Urban W 1975 Adv.Phys.24 793

[17]Wybourne B G 1966 Phys.Rev.148 317

[18]Newman D J,Ng B 1989 Rep.Prog.Phys.52 699

[19]Siu G G,Newman D J 1982 J.Phys.C:Solid State Phys.15 6753

[20]Newman D J,Ng Betty 2000 Crystal Field Handbook(Cambridge:Cambridge University Press)p83

[21]Chen X Y,Luo Z D 1999 Chin.Phys.8 607

[22]Zheng W C,Yang W Q,Liu H G 2011 Phil.Mag.91 4045

[23]Yang W Q,Zheng W C 2011 Spectrochim.Acta A 79 1291

[24]Yang W Q,Lin Y,Zheng W C,Zhao X Y 2012 Supercond.Sci.Technol.25 065011

[25]Garmen E,Daniels E,King J S 1971 J.Chem.Phys.55 1093

[26]Nassif V,Carbonio R E 1999 J.Solid State Chem.146 266

[27]Buckmaster H A,Shing Y H 1972 Phys.Status Solidi A 12 325

[28]Gschneidner K A,Eyring J L 1996 Handbook of the Physics and Chemistry of Rare Earths(Vol.23)(Amsterdam:Elsevier)p155

[29]Abragam A,Bleaney B 1970 Electron Paramagnetic Resonance of Transition Ions(London:Oxford University Press)p18,277

[30]Zhang S Y 2008 Spectroscopy of Rare Earth Ions(Beijing:Science Press)(in Chinese)[张思远2008稀土离子光谱学(北京:科学出版社)]

[31]Bravo D,Lepez F J 1993 J.Chem.Phys.99 4952

[32]Brito H F,Liu G K 2000 J.Chem.Phys.112 4334

[33]Hutchison C A,Judd B R,Pope D F D 1959 Proc.Phys.Soc.B 70 514

[34]Magnani N,Amoretti G,Baraldi A,Capelletti R 2002 Eur.Phys.J.B 29 79

[35]Magnani N,Amoretti G,Baraldi A,Capelletti R 2002 Radiat.Eff.Defect.Solids 157 921

[36]Lide D R 2003 CRC Handbook of Chemistry and Physics(84th)(Boca Raton:CRC Press)pp12–14

[37]Zheng W C 1995 Physica B 215 255

[38]Newman D J 1977 Aust.J.Phys.30 315

[39]Liu H G,Zheng W C,Feng W L 2008 Phil.Mag.88 3075

[40]Yang W Q,Zheng W C 2011 Spectrochim.Acta A 79 1291