Erdös Rényi随机网络上爆炸渗流模型相变性质的数值模拟研究*

李炎 唐刚 宋丽建 寻之朋 夏辉 郝大鹏

(中国矿业大学理学院物理系,徐州 221116)

1 引言

渗流模型是处理强无序和随机几何结构的十分有效的理论模型,它为处理无序系统中由于相互关联程度的变化所引起的相关效应提出了清晰、明确和直观的理论方法[1].渗流模型目前已经广泛应用于统计物理、凝聚态物理、生物学以及诸多工程技术领域,如被用来描述电阻丝网络[2]、森林火灾[3]、疾病传播[4]、生物进化[5]以及社会影响力等[6].

对渗流的理论研究通常采用网络模型.在一般的渗流过程中,各条键随机独立地被占据,当键的占据率达到一个与系统结构有关的阈值pc时,网络中会出现一个宏观尺度的渗流集团,此时系统经历了一个连续相变,或者说是二级相变.这种相变是随机渗流的一个基本特征,它可以发生在任何存在渗流现象的网络结构中[7],在本文中,将讨论Erdös Rényi(ER)随机网络[8]中的渗流过程.如图1所示,ER随机网络作为一种典型的无规则网络,其中的渗流过程可以描述为:从网络中N个孤立的格点开始,每一步以相同概率随机地选择两个格点,然后在这两个格点间添加一条键,即每一步随机占据一条键,这个过程依次重复进行.假设某一时刻已经有t条键被添加,将网络中的键占据率p定义为p=t/N,同时将通过占据键相互连接起来的一系列格点形成的组分称为集团,集团尺寸则被定义为集团中所包含的格点数目.对于ER网络,选取成对格点时对格点之间的距离并没有限制,而只需要记录随时间变化的集团尺寸分布.随着键的添加,集团之间相互合并,网络中的最大集团尺寸smax做动态改变.将以上随机过程中的集团生长模型称为随机生长(random growth,RG)模型,在无限大尺寸极限下,对RG模型,当 p＜1/2时,smax～logN;当p＞1/2时,smax～N,特别地,当 p略大于1/2时,smax≈(4p−2)N,最大集团尺寸在pc=1/2处经历了一个连续相变.

随机渗流模型的相变几乎都是二级[8,9]或者二级以上的[9,10],而Achlioptas等[11]则证实,通过对ER网络上具有连续相变性质的RG模型进行微小的动力学修正,可以使其表现出一级相变特征,即发生不连续相变.如图1所示,他们考虑每一步在添加单条键时,首先随机选择两条相互独立的键(c1,c2),然后在确定的定则下留下其中的一条,舍去另一条.例如在最小乘积定则(product rule,PR)下,每一步总是留下使连接的两个集团的尺寸乘积最小的那条键,在图1的情况中,键c2被留下,而舍去的键c1依然作为随后某个时间步被占据的候选键.由于乘积定则优先合并尺寸较小的两个集团,网络中集团尺寸分布相对均匀,最大集团的生长受到一个强加的延迟,当将要达到相变点时,少数几条键的添加就能导致最大集团尺寸的急剧增加,这个过程发生的时间极短,类似于火山喷发或地震爆发,因此就被称为爆炸渗流相变.本文将最小乘积定则下发生爆炸渗流相变的模型称为PR模型,以

max率差值表示相变宽度∆/N,在无限大系统尺寸极限下,对RG模型,∆/N→C,C为常数;而对PR模型,∆/N→0[11],这表明了两种模型相变性质的不同.

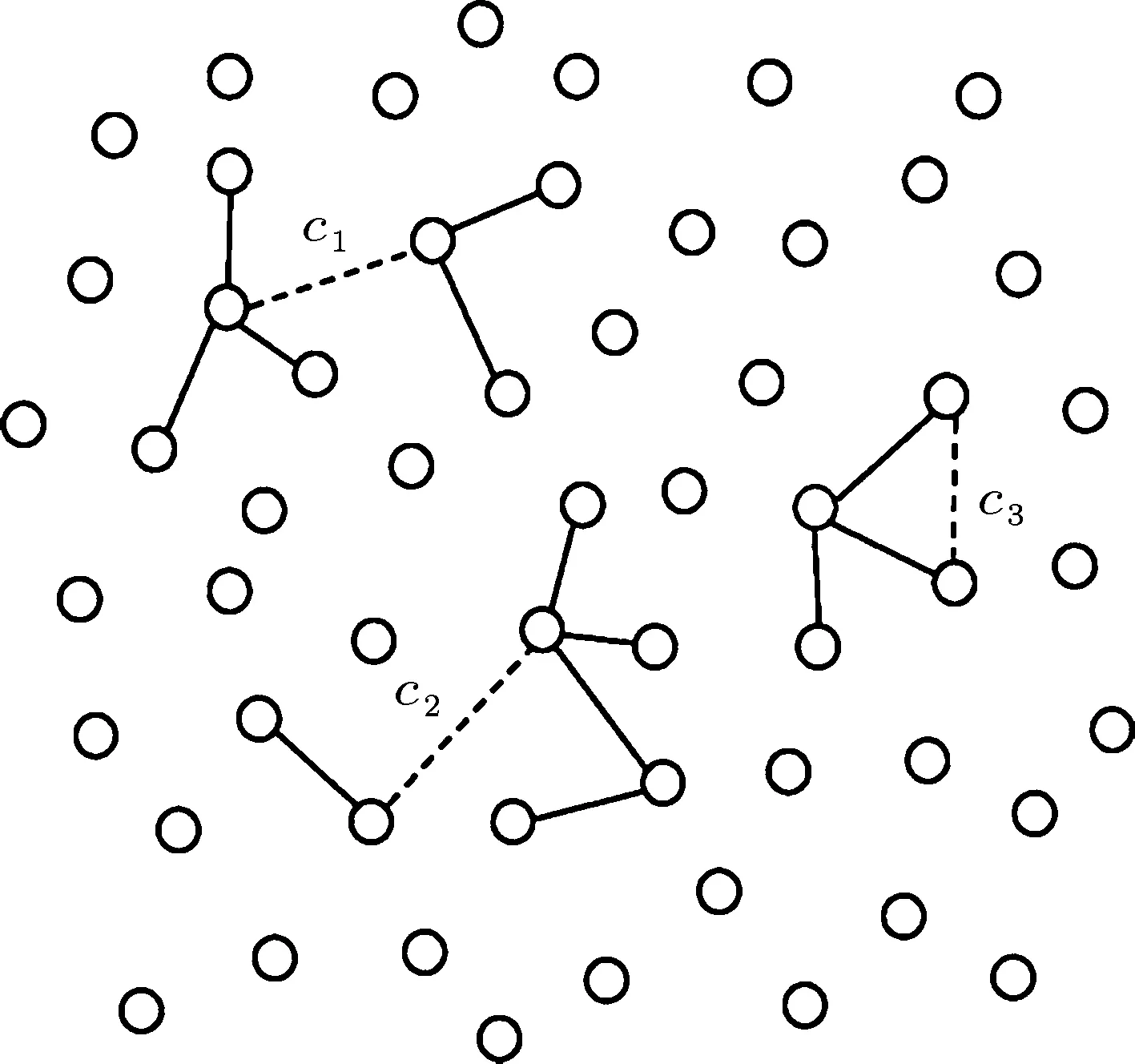
图1 ER随机网络上的集团演化示意图

ER随机网络上表现出不连续相变特征的爆炸渗流相变,吸引了众多研究者的极大兴趣,并开展了广泛的理论研究[12−26].Ziff[12,13]通过把乘积定则引入二维正方形网络同样得到了爆炸相变;Radicchi等[14]和Cho等[15]则分别采用不同的构造模型,分析了Achlioptas生长过程下无标度网络上的渗流过程,发现当度指数λ取值一定时,无标度网络也会出现爆炸渗流现象.几乎所有得到不连续爆炸相变的方法都集中于最大集团的演化方式,在有的模型中,一些研究者试图保持集团尺寸的均匀分布[16],另一些研究者则是抑制处于集团内部的键的占据[17].此外,对于同一种网络结构,在最小集团定则[18]、近邻边定则及三角边定则[19]的作用下,或者将文献[11]中“两键择一”扩展为“多键择一”[20−22],均可以得到清晰的爆炸相变.然而,爆炸渗流相变是否为不连续相变近来却一直处于争议之中[23−26].其中,Grassberger等[23]讨论了四种可以产生爆炸渗流的Achlioptas过程,根据测量的序参量分布,他们认为即使在低维系统中,相变也可以是连续的.而da Costa等[26]则是提出了一个具有代表性的爆炸渗流模型,基于对集团尺寸的计算,发现这种模型在渗流相变点处系统并没有任何的不连续性.至此,爆炸渗流相变的特性问题已经成为统计物理学领域最具争议和亟待解决的问题.

为了进一步探究Achlioptas过程下爆炸渗流模型的相变性质,本文将研究ER随机网络上Achlioptas机制下最初发生爆炸渗流现象的PR模型.通过对PR模型中表征渗流过程的基本物理量,包括序参量、平均集团尺寸、二阶矩、标准偏差及尺寸不均匀性的分析,并与RG模型的结果(研究发现,在渗流相变点处该模型以上物理量都遵循作为连续相变基本特征的幂律标度行为)比较,以此直观地反映爆炸渗流现象的相变本质.在计算中,本文采用改进了的Newman和Ziff算法以及有限尺寸标度理论,对ER随机网络上Achlioptas过程下的PR模型进行详尽的数值分析.具体地,计算了各特征物理量随键占据率p变化的分布特征,以及这些物理量在相变点处的临界标度行为,并同时给出RG模型的结果.通过对两种模型标度行为的比较分析,发现Achlioptas过程对渗流物理量的分布特征产生了显著的影响,特别是序参量具有一级相变的特征,而各渗流物理量在相变点处却表现出连续相变的幂律标度行为,这表明PR模型中的爆炸渗流相变并不是一个标准的不连续相变,不连续特征和幂律标度行为相互矛盾的结合使爆炸渗流相变成为了一种奇异相变.

2 数值计算方法

本文考虑的ER随机网络的结构,从标记为i=1,···,N的N个格点开始,每一条键都从网络上所有可能存在的键中随机选取.我们采用Newman和Ziff算法[27,28]对RG模型和Achlioptas过程下的PR模型进行模拟,每个不同的集团都用一个惟一的标签标记,通过“并查”算法来合并集团.不过与常规Newman和Ziff算法所不同的是,我们对每条键都生成一个与连接的任意两格点惟一相关的键值,这个值为[1,N(N−1)/2]内的整数,并用随机选取的键值来代替Newman和Ziff算法中以随机数生成的键占据顺序,这样既不影响结果的精度,又能提高常规Newman和Ziff算法的计算效率.选取尺寸分别为N=28,210,212,214,216,218,220的系统进行集团的动态生长,统计平均次数在103—105,其中,Radicchi和Fortunato[29]在对ER随机网络的模拟中,键占据率只能处于0,1之间,而在我们的定义中,键占据率p的最大值为(N−1)/2.另外,在乘积定则下,当选择的一条键连接的是集团内部的两个格点时,如图1中c3键,取这条键的权重为其所属集团的尺寸平方.

本文采用有限尺寸标度理论[30]来分析渗流物理量在相变点处的标度行为.有限尺寸标度理论广泛用于相变的数值分析,对连续相变,由于系统的关联长度在阈值pc处无限大,pc附近的每个物理量R都与系统尺寸无关,并且

这里ω是一个临界指数.在一个尺寸为N的有限系统上,变量R在阈值附近具有下列标度形式:

这里ν是表征关联长度的临界指数,F是一个普适函数.当 p=pc时,R ～ N+(−)ω/ν,由此得以确定临界指数比ω/ν.如果 pc,ω和ν都已知,通过做出RN−(+)ω/ν关于 (p− pc)N1/ν变化的函数曲线,可以得到普适函数F.由于F并不依赖N,所以对不同的系统尺寸,各条曲线能够很好地塌缩到一条曲线上.

3 计算结果与讨论

3.1 序参量

对无法定义自由能的非平衡问题,相变类型仍然可以根据序参量来判定[31].若序参量在相变点处骤增,相变为一级相变;否则,相变被标识为连续相变.相比于规则网格,一般的网络结构并没有渗流集团的概念,在ER网络这类随机图中,若用最大集团来代替渗流集团,〈smax/N〉即表示通常的序参量渗流概率P∞.

图2给出了不同系统尺寸下P∞随占据率p变化的函数曲线,从左到右各条曲线分别对应的系统尺寸依次增加.由图2可以看出,随着系统尺寸的增加,RG模型的序参量一直保持平缓增长,而对PR模型,在较小尺寸时,序参量呈现平缓增长,在较大尺寸时,则呈现尖锐变化,出现爆炸渗流相变,并且不同系统尺寸下的序参量变化曲线在相变点附近交叉聚合为一点.此外,当系统尺寸增大到一个确定值时,两种模型的P∞-p曲线都完全重合为一条曲线,由此可以预测对于更大的系统尺寸,序参量都不再受有限系统尺寸的影响.以上计算结果说明两种模型的序参量在相变点处具有明显不同的临界行为,这就反映了最小乘积定则的引入确实改变了网络中集团的动力学演化方式,在足够大的系统尺寸下,当达到相变点时,相比于表现出连续相变的RG模型,PR模型中序参量在相变点处尖锐变化,表现出了一级相变的特征.

图2 ER随机网络上P∞随键占据率p变化的关系曲线,图中从左到右各条曲线对应的系统尺寸N分别为28,210,212,214,216,218,220 (a)RG模型;(b)PR模型

图3给出了RG模型和PR模型的序参量P∞在pc处随系统尺寸N变化的双对数关系曲线,这里RG模型和PR模型的渗流阈值pc分别取0.5和0.888.由图3中相应线性拟合直线的斜率可以得到各模型序参量的有限尺寸标度指数比−β/ν.在误差允许的范围内,对RG模型,β/ν=0.326±0.004.事实上,对于不连续相变,有限尺寸标度理论将不再适用,此时,PR模型的序参量指数比β/ν应为零.而根据我们的计算结果,对PR模型,序参量随系统尺寸N以斜率β/ν=0.022±0.001的近乎平坦的曲线变化,这也和以上在相变点处观察到的序参量急剧变化的现象相符合.这里PR模型中β/ν的微小性使得爆炸渗流相变很难与一个不连续相变相区分,但是其非零的数值又表明,对这种相变,表征连续相变特征的幂律标度行为仍然存在,由此可以判断PR模型中的爆炸渗流相变并不是标准的不连续相变.

图3 ER随机网络上P∞(○)以及平均集团尺寸S(□)随系统尺寸N变化的双对数关系 (a)RG模型;(b)PR模型

3.2 平均集团尺寸

平均集团尺寸可以描述系统中集团尺寸的均匀程度,被定义为

其中,ns(p)为集团尺寸分布函数,上式求和不包括最大集团的尺寸.

图4给出了不同系统尺寸下RG模型和PR模型的平均集团尺寸S随键占据率p变化的函数曲线,从下到上各条曲线分别对应的系统尺寸逐渐增加.比较图4中(a),(b)两图,可以清晰地观察到,在相同的系统尺寸下,PR模型的平均集团尺寸总要比RG模型大.这个结果表明对PR模型,由于集团演化受到最小乘积定则的约束,使得网络中最大集团的尺寸并不明显地比平均集团尺寸大,各个集团的尺寸能够保持相对均匀.而RG模型中最大集团以完全随机的方式生长,由此导致在系统尺寸一定时,Achlioptas过程的平均集团尺寸与随机过程差别显著.

图4 ER随机网络上S随键占据率p变化的关系曲线,图中从下到上各条曲线对应的系统尺寸N分别为28,210,212,214,216,218,220 (a)RG模型;(b)PR模型

渗流阈值pc处两种模型的平均集团尺寸S随系统尺寸N变化的双对数关系如图3所示,图3中相应的线性拟合直线的斜率对应平均集团尺寸的有限尺寸标度指数比γS/ν,RG模型和PR 模型的 γS/ν 分别为 γS/ν=0.339±0.002和γS/ν=0.482±0.004,由以上结果可知,对Achlioptas过程下的PR模型,其平均集团尺寸同样遵循连续相变的幂律标度定律,并且由于定则的引入促进了集团尺寸的均匀分布,使得幂律关系中PR模型的标度指数比稍大于RG模型的结果.另外,通过计算发现,RG模型的β/ν和γS/ν的值近似满足超标度关系γS/ν+2β/ν=1[32],而在PR模型中这个关系却不成立,这表明对于以PR模型为代表的一类爆炸渗流模型,尽管其特征物理量仍然满足幂律标度行为,但已经与表现出连续相变的常规随机渗流模型处于不同的普适类.

3.3 二阶矩和标准偏差

在渗流模型中,将二阶矩定义为M2(p)=∑ss2ns(p)=(1/N)2,其中si为第i个格点所属集团的尺寸.图5给出了不同系统尺寸下M2(p)/N随键占据率p变化的函数曲线.根据定义,二阶矩又可以表达为M2(p)=(smax+S)·p,从以上关系看,M2(p)描述的是系统中总集团尺寸的变化趋势.对照图5中的(a),(b)两图,在相同的系统尺寸下,两种模型中的M2(p)/N随键占据率p的增加都呈逐渐增大的趋势,所不同的是,随着系统尺寸依次增加,随机过程中RG模型的M2(p)/N一直保持平缓增长,而Achlioptas过程下PR模型的情况,则是从平缓到尖锐变化,此外,PR模型的各条曲线又一次在相变点附近交叉聚合为一点.相同地,当系统尺寸大于某一个确定值后,两种模型的二阶矩都不再受有限系统尺寸的影响.以上计算表明,PR模型中键添加方式的非随机性也对网络中的总系统尺寸产生了显著影响.当系统尺寸足够大时,在渗流阈值附近,由于最大集团尺寸的剧增,导致了二阶矩曲线的骤变.类似于序参量的变化趋势,二阶矩的这种特征再一次反映了爆炸渗流相变性质的特殊性.

图5 ER随机网络上M2(p)/N随键占据率p变化的关系曲线,图中从左到右各条曲线对应的系统尺寸N分别为28,210,212,214,216,218,220 (a)RG模型;(b)为PR模型

M2(p)/N在相变点pc处的标度行为如图6所示,以−γM/ν表示其有限尺寸标度指数比.根据图6中相应的线性拟合直线的斜率,可得到RG模型中γM/ν=0.662±0.002,PR模型的计算数据也显示遵从幂律行为,为γM/ν=0.122±0.001.说明两种模型在不同的键添加方式下,虽然PR模型的二阶矩随键占据率的改变表现出不同的分布特征,但是对二阶矩标度行为的计算中,连续相变中的有限尺寸标度定律依然成立.

标准偏差χ为表征系统中最大集团尺寸smax涨落大小的物理量,定义为

图7给出了不同系统尺寸下标准偏差χ/N随占据率 p变化的函数曲线.如图7(a)所示,对RG模型,χ/N随着系统尺寸的增加逐渐减小,而图7(b)中PR模型的情况则是χ/N随系统尺寸的增加逐渐增大,并且在无限大系统尺寸下,χ/N在相变点 pc处骤增,其峰值为一个常数.假设以−λχ/ν作为比标准偏差χ/N的有限尺寸标度指数比,从χ的定义以及〈smax〉/N在 pc处的标度行为,可以推导出λx/ν=β/ν.如图6中所示,在RG模型中,χ(pc)/N 以N−0.321±0.003减小为零,即λx/ν=0.321±0.003,在误差允许的范围内,λx/ν≈β/ν,满足推导关系.对于PR模型,系统尺寸足够大时,λx/ν近似为零,且χ/N的峰值达到一个稳定值χ/N=0.265±0.002.这表明在定则的作用下,最大集团的生长受到强加的延迟,当键占据率达到阈值时,尺寸均匀的集团之间通过合并,导致最大集团的尺寸瞬间增加,尺寸涨落达到最大,并且不再受有限尺寸效应的影响.同样地,PR模型中χ/N在相变点pc处又一次表现出幂律标度行为,且与其随占据率p变化的分布特征相符合.

图6 ER随机网络上M2/N(○)以及χ/N(□)随系统尺寸N变化的双对数曲线 (a)RG模型;(b)PR模型

3.4 集团尺寸不均匀性

最近,Lee等[25]首次提出用集团不均匀性H的概念来表征渗流相变,这里H被定义为不同集团尺寸的数目.考虑集团尺寸分布函数ns,当p=0时,所有的格点都是尺寸为1的孤立集团,分布函数ns具有单分散性,H=0;在亚临界相,随着p的增加,集团之间相互合并形成更多尺寸不同的集团,集团尺寸分布变得宽泛.进入超临界相后,有限尺寸的集团逐渐被并入无限大集团,不同尺寸的集团数目减少,H逐渐减小.因此可以预测,H可能在渗流相变点附近达到一个最大值.Noh等[33]研究了d=2,3,···,6维的正方形网格和三角形网格中常规点渗流和键渗流的集团不均匀性,并建立了它们的有限尺寸标度形式.我们基于二维ER随机网络,得到了RG模型和PR模型的集团不均匀性H随占据率p变化的函数曲线,如图8所示.将图8中各条曲线的峰值记为(p∗,H∗),正如预测的那样,对于RG模型,不同系统尺寸下的p∗几乎等于阈值pc.这说明由于集团演化的完全随机性,导致了在不同的系统尺寸下,不同集团的数目即集团不均匀性都会在阈值处达到最大的统计结果.而PR模型的情况则是,p∗随着N的增加而向pc逐渐靠近,当系统尺寸足够大时,p∗等于相应的渗流阈值pc,这个结果表明了虽然定则的引入会抑制集团尺寸间的较大差异,由此减小了集团不均匀性,但是随着系统尺寸的增加,这种影响逐渐降低.

图7 ER随机网络上χ/N随键占据率p变化的关系曲线,图中从上到下各条曲线对应的系统尺寸N分别为28,210,212,214,216,218,220 (a)RG模型;(b)PR模型

假设H的有限尺寸标度指数比用γH/νH来表示,根据标度理论,当 p=p∗时,(pc−p∗)N1/νH为一个确定的常数,并且在这一点,H∗～NγH/νH.由以上标度假设,在图9中给出了(pc−p∗)-1/N以及H∗-N的双对数关系曲线.由线性拟合直线的斜率可以得到,对 RG 模型,1/νH=0.205±0.002,γH/νH=0.397±0.001;对 PR 模型,1/νH=0.378±0.003,γH/νH=0.484±0.002.根据计算所得的标度指数,分别做出两种模型的 HN−λH/νH-(p− pc)N1/νH变化曲线,如图10所示.此时图8中不同系统尺寸下的H-p曲线都极好地塌缩到一条曲线上,这表明PR模型的集团不均匀性也表现出了很好的标度特征,适用于连续相变的有限尺寸标度规律仍然可用于描述集团不均匀性的标度行为.

图8 ER随机网络上H随键占据率p变化的关系曲线,图中从下到上各条曲线对应的系统尺寸N分别为28,210,212,214,216,218,220 (a)RG模型;(b)PR模型

图9 ER随机网络上(pc−p∗)随1/N以及H∗随N变化的双对数关系 (a)pc−p∗-1/N;(b)H∗-N

图10 ER随机网络上集团不均匀性H的标度分析曲线 (a)RG模型,(b)PR模型

4 结论

基于改进了的Newman和Ziff算法以及有限尺寸标度理论,本文对ER随机网络上PR模型的相变过程进行了数值研究.通过对表征渗流相变基本物理量,包括序参量、平均集团尺寸、二阶矩、标准偏差及尺寸不均匀性进行详尽的计算分析发现,PR模型中以上渗流物理量随键占据率变化的分布特征与RG模型的结果有显著差别.特别地,在足够大的系统尺寸下,PR模型的序参量在渗流相变点处呈现出具有不连续相变特征的尖锐跃变,然而包括序参量在内的各个渗流量在相变点处却都表现出连续相变的幂律标度行为.因此严格地说,PR模型中的爆炸渗流相变是一种奇异相变,它既不是一个标准的不连续相变,又与RG模型表现出的典型连续相变处于不同的普适类.

另外,与热力学相变相比,渗流相变是由于系统几何结构的改变导致它的某种性质发生突变的现象,即是一种几何相变,那么这种几何相变的阶数不能被严格限定.在一级相变与二级相变之间,可能会存在交叉混合相变,如Achlioptas过程下爆炸渗流模型的奇异相变.此外,爆炸渗流的本质问题之所以会存在争议,还在于研究者考虑的切入点的不同.鉴于此,爆炸渗流模型相变类型的统一判据也是今后值得研究的问题.

[1]Zalle R(translated by Huang Y)1998 Amorphous Solid State Physics(Beijing:Peking University Press)(in Chinese)[Zalle著 (黄畇译)1998非晶态固体物理学(北京:北京大学出版社)]

[2]de Arcangelis L,Redner L,Coniglio A 1985 Phys.Rev.B 31 4725

[3]Henley C L 1993 Phys.Rev.Lett.71 2741

[4]Moore C,Newman M E J 2000 Phys.Rev.E 61 5678

[5]Jovanović B,Buldyrev S V,Havlin S,Stanley H E 1994 Phys.Rev.E 50 2403

[6]SolomonS,WeisbuchG,deArcangelisL,JanN,StaufferD2000Physica(Amsterdam)277A 239

[7]Stauffer D,Aharony A 1991 Introduction to Percolation Theory(2nd Ed.)(London:Taylor and Francis)

[8]Erdös P,Rényi A 1960 Publ.Math.Inst.Hungar.Acad.Sci.5 17

[9]Callaway D,Hopcroft J,Kleinberg J,Newman M,Strogatz S 2001 Phys.Rev.E 64 041902

[10]Kim J,Krapivsky P,Kahng B,Redner S 2002 Phys.Rev.E 66 055101

[11]Achlioptas D,Souza R M D,Spencer J 2009 Science 323 1453

[12]Ziff R M 2009 Phys.Rev.Lett.103 045701

[13]Ziff R M 2010 Phys.Rev.E 82 051105

[14]Radicchi F,Fortunato S 2009 Phys.Rev.Lett.103 168701

[15]Cho Y S,Kim J S,Park J,Kahng B,Kim D 2009 Phys.Rev.Lett.103 135702

[16]Araújo N A M,Herrmann H J 2010 Phys.Rev.Lett.105 035701

[17]Moreira A A,Oliveira E A,Reis S D S,Herrmann H J,Andrade Jr J S 2010 Phys.Rev.E 81 040101(R)

[18]Friedman E J,Landsberg A S 2009 Phys.Rev.Lett.103 255701

[19]Souza R M D,Mitzenmacher M 2010 Phys.Rev.Lett.104 195702

[20]Araújo N A M,Andrade Jr J S,Ziff R M,Herrmann Jr H 2011 Phys.Rev.Lett.106 095703

[21]Manna S S,Chatterjee A 2011 Physica(Amsterdam)390A 177

[22]Pan R K,Kivela M,Saramaki J,Kaski K,Kertesz K 2011 Phys.Rev.Lett.83 046112

[23]Grassberger P,Christensen C,Bizhani G,Son S W,Paczuski M 2011 Phys.Rev.Lett.106 255701

[24]Riordan O,Warnke L 2011 Science 333 322

[25]Lee H K,Kim B J,Park H 2011 Phys.Rev.E 84 020101

[26]da Costa R A,Dorogovtsev S N,Goltsev A V,Mendes J F F 2010 Phys.Rev.Lett.105 255701

[27]Newman M E J,Ziff R M 2000 Phys.Rev.Lett.85 4104

[28]Newman M E J,Ziff R M 2001 Phys.Rev.E 64 016706

[29]Radicchi F,Fortunato S 2010 Phys.Rev.E 81 036110

[30]Landau D P,Binder K 2000 A Guide to Monte Carlo Simulations in Statistical Physics(England:Cambridge University Press)

[31]Ódor G 2004 Rev.Mod.Phys.76 663

[32]Cohen R,ben-Avraham D,Havlin S 2002 Phys.Rev.E 66 036113

[33]Noh J D,Lee H E,Park H 2011 Phys.Rev.E 84 010101