α-Ti2Zr高压物性的第一性原理计算研究*

张品亮1) 龚自正1)2)† 姬广富3) 刘崧1)

1)(西南交通大学材料科学与工程学院,材料先进技术教育部重点实验室,成都 610031)

2)(北京卫星环境工程研究所,可靠性与环境工程技术国防科技重点实验室,北京 100094)

3)(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理国防科技重点实验室,绵阳 621900)

(2012年9月10日收到;2012年10月29日收到修改稿)

1 引言

IV族金属及其合金具有高的比强度、耐腐蚀、较好的高低温性能[1],因此引起科学界和工程应用界的广泛关注.目前,Ti-Zr合金已经广泛应用于航空航天、医学、核工业等领域.Ti-Zr合金存在多种相结构[2,3],在室温下通常以密排六方(hcp)结构的α相形式存在;随着压力的增加,α相转变为六方结构的ω相;当达到一定压力时,形成具有体心立方(bcc)结构的β相.研究表明,压力诱导电子从s轨道转移到d轨道决定了压力下结构的稳定性[4].因此,研究高压下α-Ti2Zr合金中电子的分布情况,对确定高压下的稳定相具有重要作用.

体积模量、剪切模量和杨氏模量等是重要的物性参数,研究高压下α-Ti2Zr合金的这些参数,对Ti2Zr合金在高压环境下的性能评价和应用具有重要意义.

目前对IV族金属及其合金已做了大量研究,

但是主要集中在 Ti[5−9],Zr[4,10−14]和 TiZr[15,16],很少涉及Ti2Zr.虽然α-Ti2Zr合金已经在实验中制备得到,并且测量了它的晶格参数[17−19].但是关于它的弹性常数和热力学性能,特别是高压下这些物性参数的变化还没有相关报道.随着计算机技术的迅速发展,第一性原理平面波赝势方法已经广泛应用于材料结构和性能的计算研究中[20−25],如王斌等[23]利用第一性原理计算了TiC的弹性常数和热力学性质;陈中钧等[24]采用此方法研究了MgS的弹性性能,电子结构和光学性质;Zhu等[25]计算研究了TiO2在高压下的弹性性能.因此,本文基于第一性原理方法计算研究了α-Ti2Zr的结构、弹性常数、德拜温度以及压力诱导下电子的分布情况等.

2 计算方法

2.1 参数设置

第一性原理计算采用了基于密度泛函理论(DFT)的平面波赝势法,所用软件为CASTEP[26].计算中,电子之间相互作用的交换关联势采用了广义梯度近似(GGA)的Perdew-Burke-Ernzerhof(PBE)势[27];离子实和价电子之间的相互作用采用超软赝势[28];平面波截断能为550 eV;K点为18×18×4.几何优化采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法,收敛标准为每原子总能量偏差＜10−5eV,原子的最大Hellmann-Feynman力＜0.03 eV/Å,最大应力偏差＜0.05 GPa,最大位移偏差＜0.001Å.

2.2 弹性常数

体积模量B和剪切模量G可通过Viogt-Reuss-Hill(VRH)方法获得[29].对于具有六方结构的晶体,B和G可以表示为[30]

其中

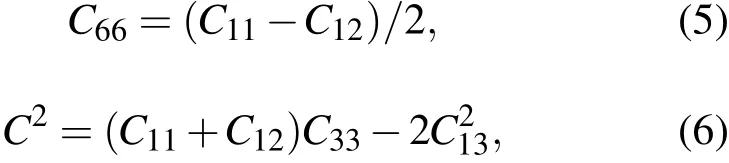
以上式中Cij为独立弹性常数.取Voigt值和Reuss值的算术平均,得到Hill值[31]:

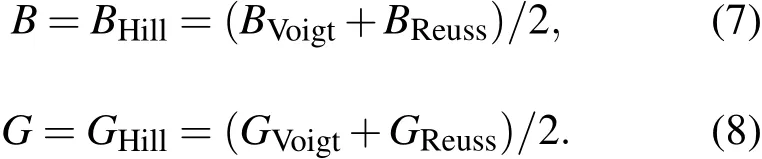
杨氏模量E和泊松比σ可从以下关系推出:

3 结果和讨论

3.1 晶格常数

本文中所建立的α-Ti2Zr为1×1×3的超胞结构,具有6个原子,采用ReB2类型的晶体结构[32],如图1.在开始计算之前,我们做了大尺度效应的验证.根据对称性计算了两种大晶胞(2×1×3和1×1×6的超胞)的总能量EGE,这两种结构中每个原子的能量为:−1495.6958872和−1495.6958873 eV,结果与本文所采用结构(−1495.6958872 eV)相同,说明本文所采用的结构虽为最小晶胞,但不存在大尺度效应.

通过比较总能量EGE可以获得在零压下的平衡结构参数,而通过拟合EGE-V关系可以得到体积模量B0和体积模量对压力的一阶偏导数,下标“0”表示在零温零压下的值.根据α-Ti2Zr的实验c/a值1.593,计算了一系列c/a值下不同晶格常数相应的总能量EGE和原胞体积V,用Birch-Murnaghan状态方程[33]进行拟合,最终得到的晶格常数a和c,B0和列于表1,同时,表1中还列出了实验测量结果.对比后发现,计算结果与实验结果相一致,可认为我们的计算是可靠的.

图1 α-Ti2Zr的结构

表1 α-Ti2Zr的晶格常数a,c,B0和

表1 α-Ti2Zr的晶格常数a,c,B0和

a/Åc/Åc/aB0/GPaB′0本文 3.032 4.877 1.608 99.3 3.4实验结果[17] 3.051 4.859 1.593

图2为α-Ti2Zr的晶格常数与压力的关系,下标“0”表示在零压下的值.对于α-Ti2Zr,较弱的原子键Zr—Zr决定晶格参数a,因此在高压作用下,a轴方向的压缩率明显大于c轴方向.

图2 a/a0,c/c0和V/V0与压力P的关系

3.2 弹性常数

单晶的弹性常数可以通过计算能量EGE的二阶偏导数获得[34,35]:

其中V为原胞体积;ε是应变张量,通过材料的变形来获得弹性常数.对于晶体,有21个独立的弹性常数,但是根据晶体的对称性可以将它们减少.对于六角晶系的α-Ti2Zr,存在5个独立弹性常数:C11,当它们符合条件[36,37]C44＞0,时,才能够稳定存在.计算结果表明:α-Ti2Zr在0—25 GPa压力范围内稳定存在.

图3为α-Ti2Zr的独立弹性常数与压力的关系.从图3中可以看出C11,C33,C12,C13均随着压力的升高而增加,只有C44随着压力的升高而降低.对于过渡金属,C11和C33非常重要,它们与原子键和变形行为有关.C33＞C11表明{001}面上的原子键强于{100}面上的原子键.

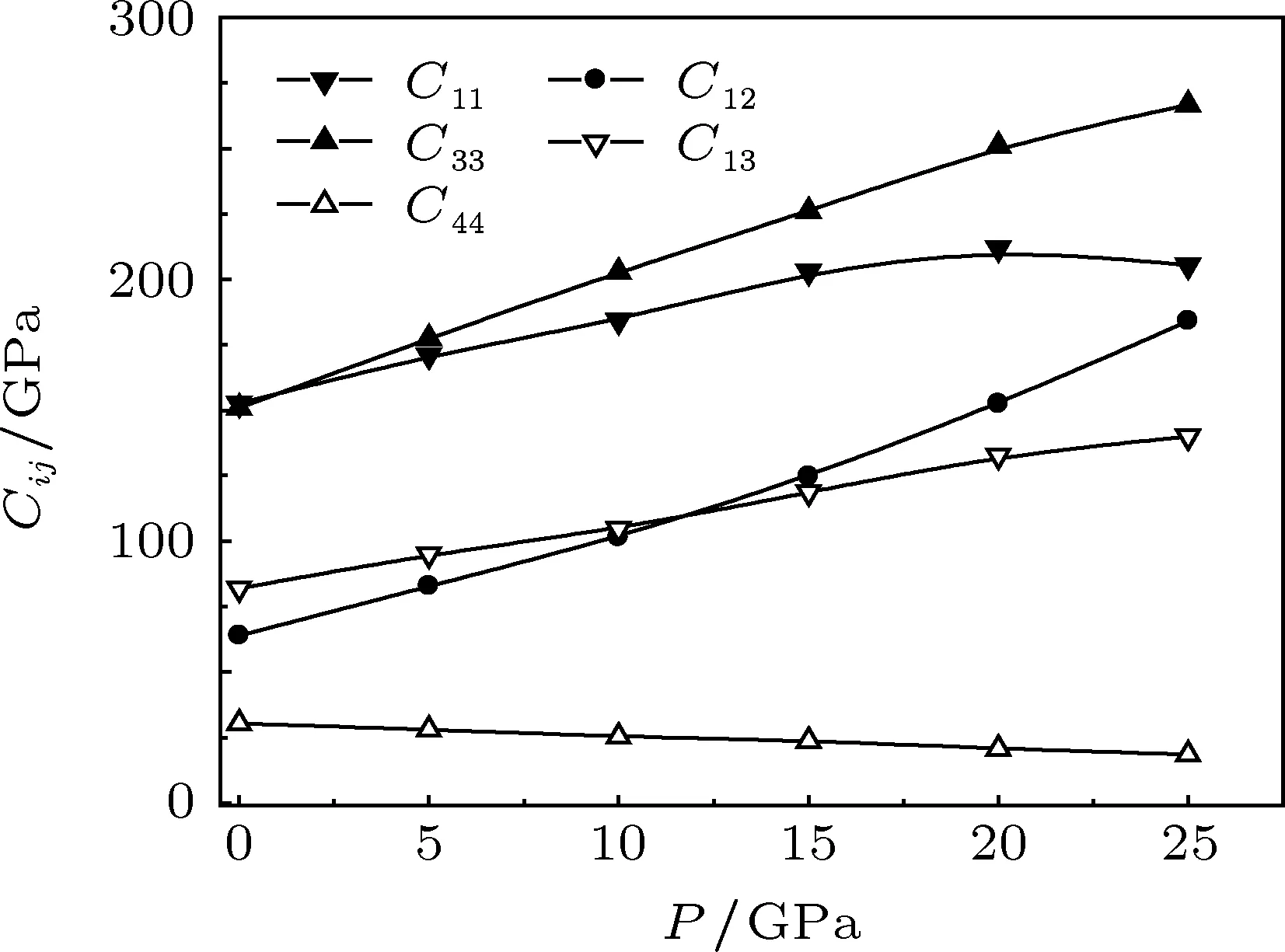
图3 独立弹性常数Cij与压力P的关系

表2为计算得到的体积模量B、剪切模量G、杨氏模量E和泊松比σ,为便于对比,α-Ti,α-Zr以及α-TiZr的参数也在表2中给出.由表2可见,α-Ti的体积模量B、剪切模量G和杨氏模量E最大,α-Ti2Zr的值介于α-Ti和α-Zr之间.它们的泊松比σ基本一致.因此,可通过调节Ti-Zr系合金的组成元素含量实现对其弹性常数的控制.图4为B和G随压力的变化趋势,从图4中可以看出,B随着压力的升高而迅速增加,G则随着压力的升高而减小.

图4 体积模量B和剪切模量G与压力P的关系

表2 α-Ti2Zr,α-Ti,α-Zr和α-TiZr的体积模量B,剪切模量G,杨氏模量E,泊松比σ和G/B

图5 α-Ti2Zr的G/B比值与压力P的关系

体积模量B和剪切模量G决定着材料的抗塑性变形和抗断裂能力.Pugh[39]基于弹性常数提出一种预测材料脆性和延展性的经验公式:R=G/B.如果R＞0.57,材料表现为脆性;反则具有较好的延展性.从表2中可看出α-Ti2Zr的R＜0.57,具有较好的延展性.此外,α-Zr的延展性最好,其次为Ti-Zr合金.图5给出了R与压力的关系,随着压力的增加,R值减小.说明在压力作用下,α-Ti2Zr表现出更加优异的延展性.

3.3 各向异性

声速和弹性常数的关系服从Christoffel方程[40]:

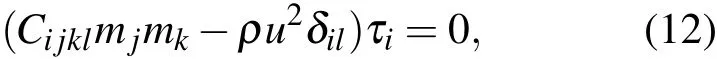
式中Cijkl为弹性常数,ρ为密度,τ为传播矢量,m为传播方向,M=ρu2为传播系数,u为速度.声速的各向异性可表示为[41]

这里mx为除了[100]方向以外的传播方向,i代表三种弹性波类型.通过解Christoffel方程,可获得α-Ti2Zr的压缩波(P)、垂直于基面的偏振波(S1)和平行于基面的偏振波(S2)的各向异性:

图6 α-Ti2Zr的各向异性与压力P的关系

根据Born和Huang[42]提出的CNNF模型,独立弹性常数比率C33:C11:C12:C13:C44=32:29:11:8:8,∆P=1.1,∆S1=1.4和∆S2=0.9.图6为压力与相关弹性波的各向异性的关系.α-Ti2Zr的零压∆P,∆S1和∆S2分别为0.99,1.15和0.68,与CNNF模型偏差较大,α-Ti2Zr在零压下表现出较大的各向异性.随着压力的增加∆P和∆S1均单调增加,∆S2先缓慢减小再迅速增加.∆P,∆S1和∆S2与CNNF模型的偏差随着压力的增加而增大,因此α-Ti2Zr在高压下同样具有较大的各向异性.

3.4 德拜温度

德拜温度是一个重要的物性参数,很多物理属性都与德拜温度有关,如比热容、热膨胀系数和熔点.德拜温度可以从弹性常数计算得到[43]:

其中h是Plank常数;kB是Boltamann常数;n是原胞中的原子数量.平均波速vm可以利用Navier方程[44]从剪切波速vs和压缩波速vp计算得到:

计算得到α-Ti2Zr合金的德拜温度为Θ=321.7 K.

3.5 压力下的s-d电子转移

IV族元素具有较窄的d轨道.在压力诱导下,s-p轨道的电子转移到d轨道对这些晶体的结构稳定性具有重要影响[45].下面采用Mulliken分布分析方法[46]讨论压力诱导α-Ti2Zr的s-d电子转移情况.图7为在加压下s,p和d轨道上电子数的变化情况,∆Ne为加压与零压下轨道上电子数之差.在压力下Ti和Zr原子中s,p轨道上的电子转移到d轨道,增加了d轨道上占据的原子数,这正好解释了表1中零压体积模量对压力的偏导数为什么较小.1983年,Vohra[47]研究了d轨道金属的柔软度,得到与轨道上电子数的关系:

图7 压力下α-Ti2Zr各层电子数的变化情况

其中Nsp表示sp轨道上的电子数. X=−dNsp/dlnV=dNd/dlnV为s↔d电子转移参数,负数表示s→d的电子转移.表示在没有电子转移情况下体积模量对压力的偏导数(X=0).可见s→d电子转移将使偏小.Bashkin等[15]认为压力诱导过渡金属发生s→d电子转移是IV族金属在压力下发生相变的原因.一些理论预计[45]当IV族金属d轨道电子数Nd＞2.2时,bcc结构的β相将更加稳定.图7表明,在压力作用下α-Ti2Zr中Ti和Zr原子d轨道的电子数随着压力的增加而增加.因此,当压力达到一定值时,α-Ti2Zr可能形成具有bcc结构的β-Ti2Zr,这正好验证了我们早期的结论:β-Ti2Zr形成于25.4—29.1 GPa[48].

4 结论

通过第一性原理计算得到了α-Ti2Zr的晶体结构、弹性常数、德拜温度和电子分布,研究了在压力作用下这些参数的变化情况.得到的结论如下:1)计算得到的晶体参数与实验结果一致,因此本文的计算是可信的;2)在零压下,α-Ti2Zr的体积模量为101.2 GPa,剪切模量为35.6 GPa,在所研究的压力下体积模量随着压力的升高而增加,与剪切模量的变化趋势相反.德拜温度为Θ=321.7 K;3)G/B＜0.57,并且随着压力的增加而减小,说明α-Ti2Zr具有较好的延展性;4)α-Ti2Zr在零压及高压下的各向异性均较大;5)Mulliken分布分析表明,当达到一定压力时,α-Ti2Zr可能转变为β-Ti2Zr.

[1]Vohra Y K,Spencer P T 2001 Phys.Rev.Lett.86 3068

[2]Murray J L 1981 Bulletin of Alloys Phase Diagrams 2 197

[3]Chatterji D,Hepworth M T,Hruska S J 1971 Metall.Trans.2 1271

[4]Liu W,Li B S,Wang L P,Zhang J Z,Zhao Y S 2007 Phys.Rew.B 76 144107

[5]Hao Y J,Zhang L,Chen X R,Li Y H,He H L 2008 Solid State Commun.146 105

[6]Mei Z G,Shang S L,Wang Y,Liu Z K 2009 Phys.Rev.B 79 134102

[7]Errandonea D,Meng Y,Somayazulu M,Häusermann D 2005 Physica B 355 116

[8]Kerley G I 2003 Sandia Report,Sand 2003-3785

[9]Hao Y J,Zhu J,Zhang L,Qu J Y,Ren H S 2010 Solid State Commun.12 1473

[10]Wang B T,Zhang P,Liu H Y,Li W D,Zhang P 2011 J.Appl.Phys.109 063514

[11]Hao Y J,Zhang L,Chen X R,Li Y H,He H L 2008 J.Phys.:Condens.Mat.20 235230

[12]Liu W,Li B S,Wang L P,Zhang J Z,Zhao Y S 2008 J.Appl.Phys.104 076102

[13]Xia H,Duclos S J,Ruoff A L,Vohra Y K 1990 Phys.Rev.Lett.64 204

[14]Zhang S H,Zhu Y,Zhang X Y,Zhang S L,Qi L,Liu R P 2010 Comput.Mat.Sci.50 179

[15]Bashkin I O,Fedotov V K,Nefedova M V,Tissen V G,Ponyatovsky E G,Schiwek A,Holzapfel W B 2003 Phys.Rev.B 68 054401

[16]Wang B T,Li W D,Zhang P 2012 J.Nucl.Mater.420 501

[17]Dolukhanyan S K,Aleksanyan A G,Ter-Galstyan O P,Shekhtman V S,Sakharov M K,Abrosimova G E 2007 Russ.J.Phys.Chem.B 1 563

[18]Shekhtman V S,Dolukhanyan S K,Aleksanyan A G,Mayilyan D G,Ter-Galstyan O P,Sakharov M K,Khasanov S S 2010 Int.J.Self-Propag.High-Temp Synth.19 40

[19]Swainson I P,Dolukanyan S K,Aleksanyan A G,Shekhtman V S,Mayilyan D G,Yonkeu A L 2010 Can.J.Phys.88 741

[20]Xu G L,Chen J D,Chen D,Ma J Z,Yu B H,Shi D H 2009 Chin.Phys.B 18 0744

[21]Hao A M,Zhou T J,Zhu Y,Zhang X Y,Liu R P 2011 Chin.Phys.B 20 047103

[22]Li D H,Su W J,Zhu X L 2012 Acta Phys.Sin.61 023103(in Chinese)[李德华,苏文晋,朱晓玲2012物理学报61 023103]

[23]Wang B,Liu Y,Ye J W 2012 Acta Phys.Sin.61 186501(in Chinese)[王斌,刘颖,叶金文2012物理学报61 186501]

[24]Chen Z J 2012 Acta Phys.Sin.61 177104(in Chinese)[陈中钧2012物理学报61 177104]

[25]Zhu J,Yu J X,Wang Y J,Chen X R,Jing F Q 2008 Chin.Phys.B 17 2216

[26]Segall M D,Lindan P J D,Probert M J,Pickard C J,Hasnip P J,Clark S J,Payne M C 2002 J.Phys.:Condens.Mat.14 2717

[27]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[28]Vanderbilt D 1990 Phys.Rev.B 41 7892

[29]Nye J F 1957 Physical Properties of Crystals(London:Oxford University Press)

[30]Watt J P,Peselnick L 1980 J.Appl.Phys.51 1525

[31]Hill R 1952 Proc.Phys.Soc.65 350

[32]Long R,Dai Y,Jin H,Huang B B 2008 Res.Lett.Phys.2008 293517

[33]Murnaghan F D 1944 Proc.Natl.Acad.Sci.USA 30 244

[34]Antonov V,Iordanova I 2009 AIP Conf.Proc.1203 1149

[35]Accelrys Software Inc.2010 Materials Studio Release Notes(Release 5.5)(Scan Diego:Accelrys Software Inc.)

[36]Born M 1940 Proc.Cambridge Philos.Soc.36 160

[37]Sin’ko G V,Smirnov N A 2002 J.Phys.:Condens.Mat.14 6989

[38]Tang W H,Zhang R Q 1999 Equation of State Theory and Calculation Conspectus(Changsha:National University of Defense Technology Press)p321(in Chinese)[汤文辉,张若棋1999物态方程理论及计算概论(长沙:国防科技大学出版社)第321页]

[39]Pugh S F 1954 Philos.Mag.45 823

[40]Auld M A 1973 Acoustic Fields and Waves in Solids(Vol.I)(New York:Wiley)

[41]Steinle-Neumann G,Stixrude L,Cohen R E 1999 Phys.Rev.B 60 791

[42]Born M,Huang K 1954 Dynamical Theory of Crystal Lattices(Clarendon:Oxford)

[43]Anderson O L 1963 J.Phys.Chem.Solids 24 909

[44]Schreiber E,Anderson O L,Soga N 1973 Elastic Constants and Their Measurements(New York:McGraw-Hill)

[45]Skriver H L 1985 Phys.Rev.B 31 909

[46]Mulliken R S 1955 J.Chem.Phys.23 1833

[47]Vohra Y K,Sikka S K,Holzapfel W B 1983 J.Phys.F:Met.Phys.13 L107

[48]Zhang P L,Gong Z Z,Ji G F 2012 Proceedings of 20th International Conference on Composites Engineering Beijing,China,July 22–28,2012