驳船升沉运动和波浪联合作用对沉管管段运动特性的影响

左卫广，王永学

（大连理工大学 海岸和近海工程国家重点实验室，大连116024）

沉管法是当前海底隧道建造施工的新方式，而沉管管段的安全沉放是沉管隧道施工的关键环节。驳船吊挂沉放法作为一种常用的沉放方式，其沉管管段的运动特性是波浪直接引起的沉管管段运动与波浪作用下驳船施工装备的运动间接引起的沉管管段运动的复合运动。驳船升沉运动和波浪联合作用下的沉管管段的沉放运动特性是一个十分复杂的水动力学问题。

目前国内外关于沉管管段的沉放运动特性研究工作大都是忽略了驳船运动的影响。詹德新［1］试验研究了沉管沉放过程中的流体作用力和缆绳缆力，考虑了流速和波高等环境因素的影响，并分析了压载水对沉管沉放稳定性的影响。Jensen［2］等建立了施工海域的波浪模型，分析了沉管的沉放运动特性，研究了近海波况对沉管隧道施工沉放的影响。陈智杰［3］对沉管管段在固定深度下的运动特性进行了试验研究，并采用边界元方法对沉管管段沉放运动进行了时域数值模拟，数值模拟结果与试验结果比较，吻合良好。

实际工程中，当沉管管段进行沉放施工时，沉管管段不仅受到波浪和水流的作用，还受到海上驳船运动的影响。驳船在波浪和水流作用下的运动，通过缆绳的传递将会对沉管运动有很大影响。本文主要研究驳船升沉运动和波浪联合作用对沉管管段运动特性的影响。建立了驳船升沉运动和波浪联合作用下沉管管段运动的数学模型，通过数值算例分析，探讨了驳船做不同振幅与不同相位升沉运动情形下的沉管管段运动特性。

1 波浪作用下沉管运动数学模型

驳船吊挂沉放法进行沉管管段沉放作业的示意图见图1。在图1 中，引入2 个坐标系统：参考坐标系O0-x0y0z0和动坐标系O-xyz。坐标平面O0-x0y0z0位于静水面，x0轴为沿沉管的长度方向，z0轴为垂直水面向上；坐标系O-xyz 与管段固结，随管段一起摇荡，x 轴为沿管段的长度方向。当管段处于平衡位置时，动坐标系Oxyz 和参考坐标系O0-x0y0z0是重合的。参考坐标系是表征沉管管段摇荡位移和姿态的基准，当管段由于外力的作用产生偏移时，偏移量由动坐标系相对于参考坐标系的运动来描述。

图1 所示的沉管管段的运动可以看作是两部分运动的合成，一部分是忽略驳船运动情形（假定吊缆上端点为固定情形）下波浪作用引起的沉管管段运动；另一部分是由驳船运动引起的沉管管段运动。

图1 沉管管段示意图Fig.1 Sketch of immersing tunnel element

本文采用直接时域法求解波浪作用引起的沉管管段运动。基于势流理论，流场的速度势满足Laplace 方程的定解问题。应用格林定理建立时域内的积分方程，使用边界元方法（Hess 和Smith［4］；Garrison［5］；Liu 等［6］；Teng 和Eatock Taylor［7］）数值求解时域内的积分方程得到速度势后，可计算出沉管管段所受到的波浪力，求解沉管管段的运动方程得到波浪作用引起的沉管管段运动响应。

1.1 流场控制方程

流场内，速度势φ 满足Laplace 方程

式中：A 为波幅；β 为浪向角；g 为重力加速度；h 为水深；k 为波数；ω 为入射波的频率；t 为时间；φm为φ，φI或φS中的任何一个；p 为流场中点的位置矢量；n 为物体表面的法向量，物面向外为正；Vn为物体表面上的法向速度。

1.2 速度势求解

本文采用格林函数法来处理速度势的求解问题。有限水深条件下时域格林函数可以表达成以下两式之和的形式［8－9］

G0和Gf分别称为瞬时项和记忆项，其定义为

式中：τ 为时间；p（x，y，z）和q（ξ，η，ζ）分别为场点和源点矢量；J0为零阶贝塞尔函数；r 为场点和源点的距离；R 为场点和源点的水平距离；r2为场点和源点关于水底面镜像的距离。

对速度势的初边值问题应用格林定理，考虑线性问题，物面边界用平均边界SB代替SB（τ），经过推导可得到在自由面SF（τ）、物面SB、海底边界SD和无穷远边界S∞组成的流体域Ω 内的时域内积分方程

应用边界元方法，数值求解时域内积分方程（10），可得到流场速度势φS。

1.3 荷载计算

沉管在沉放过程中，受到波浪力和缆绳缆力的共同作用。

波浪力可表示为

式中：ρ 为流体密度；速度势φ 包括入射势φI和散射势φS。

缆绳缆力可表示为

式中：T 为缆绳张力；Ce 为缆绳弹性系数；d 为缆绳直径；ΔS 为缆绳变形长度；S 为缆绳原始长度；n 为指数。

当缆绳为钢缆时，n＝3/2。

1.4 沉管运动方程

沉管运动方程可写为如下形式

式中：Fk为总的广义水动力荷载分量；Gk为缆绳沉放系统对沉管施加的外部作用力和力矩；M 为质量矩阵；B为系统阻尼矩阵；C 为恢复力矩阵，由于沉管位于水面以下，故静恢复力为0；ξj为第j 个模态下沉管管段的响应幅值，j=1～6 分别为沉管的纵荡、横荡、升沉、横摇、纵摇和回转运动。

沉管运动方程式可表示为如下的二阶微分方程形式

应用四阶Runge-Kutta 方法求解式（14），可得到沉管管段的位移和速度表达为

式中：M1、M2、M3和M4分别为

2 考虑驳船升沉运动情形下沉管运动数学模型

假定驳船在升沉方向做强迫简谐运动，其升沉运动方程采用如下表达式

式中：b 为驳船做升沉运动的振幅；ω 为入射波频率；θ 为驳船运动与波浪之间的相位差；tm为缓冲周期。

在t 时刻，驳船的位置为z（t），同时考虑波浪作用与驳船升沉运动影响的沉管位置为ξj（t）（j=1，2，3，4，5，6）。在t+Δt 时刻，首先考虑驳船升沉运动对沉管位置的改变。驳船在t+Δt 时刻的位置z（t+Δt），相对于t 时刻的瞬时位置变化为

在仅考虑驳船升沉运动对沉管运动的影响时，认为驳船做升沉运动瞬时缆绳长度不发生变化，即沉管升沉方向与驳船具有相同的位移变化。在t+Δt 时刻，仅考虑驳船升沉运动影响时沉管瞬时位置ξzj（t+Δt）为

驳船的升沉运动使得沉管位置由ξj（t）变成ξzj（t+Δt），沉管受到的波浪力也发生变化。数值求解对应于沉管位置ξzj（t+Δt）的速度势φS，带入波浪力公式（12），可得到沉管在位置ξzj（t+Δt）所受到的波浪力Fk′。然后分别用ξzj（t+Δt）和Fk′代替公式（16）中的ξj（t）和Fk（t），即可得到t+Δt 时刻考虑波浪作用与驳船升沉运动共同影响的沉管位置ξj（t+Δt）。

3 算例计算及分析

数值计算中取沉管尺寸的长×宽×高为100 m×15 m×10 m，沉放深度h 为8 m，水深H 为40 m。入射波为正向规则波，周期T 为5 s，波高为1.0 m。缆绳为钢缆，直径为0.3 m，缆绳弹性系数为2.75×106kg/cm2。驳船升沉运动的振幅与相位取值见表1。

表1 计算工况Tab.1 Calculated condition

首先对忽略驳船运动时的沉管运动响应进行了计算。图2 给出了忽略驳船升沉运动情形下沉管升沉运动时间过程线与入射波浪的时间过程线的比较，时间段取100～110 s（20～22 T）。图中实线为忽略驳船运动情形下沉管升沉运动时间过程线，虚线为波浪的时间过程线。由图2 可见，忽略驳船运动时的沉管升沉运动幅值约为0.1 m，沉管升沉运动过程线与入射波浪过程线相比，两者之间存在较大的相位差，相位差约为π/2。

图2 忽略驳船运动情形的沉管升沉运动时间过程线（H=1.0 m，T=5 s）Fig.2 Time history of waves and heave motion of tunnel element without barge motion（H=1.0 m，T=5 s）

图3 不同相位情形下驳船升沉运动过程线（b=0.3 m）Fig.3 Time history of barge heave motion under different phases（b=0.3 m）

参照表1 给出的计算工况，对同时考虑波浪作用与驳船升沉运动影响的沉管运动响应进行了数值计算与分析。图3 是驳船升沉运动振幅为0.3 m、驳船运动与波浪相位差分别取-π/2，-π/5，0，+π/5 和+π/2 情形的驳船升沉运动历时过程线，时间段为100～110 s（20～22 T））。由图3 与图2 可见，当驳船升沉运动与入射波浪之间的相位θ=-π/2 时，驳船升沉运动与忽略驳船运动时的沉管升沉运动之间的相位差为0；当驳船升沉运动与入射波浪之间的相位θ=π/2 时，驳船升沉运动与忽略驳船运动时的沉管升沉运动之间的相位差为π。

图4 是驳船升沉运动振幅为0.3 m、相位分别为-π/2，0 和+π/2 情形，考虑波浪作用和驳船升沉运动共同影响的沉管运动响应分量与忽略驳船运动时的沉管运动响应分量的比较。图中heave 表示沉管升沉方向运动，sway 表示沉管横荡方向运动，roll 表示沉管纵摇方向运动。

由图4 可见，当驳船做升沉运动时的沉管运动过程线与忽略驳船运动时的沉管运动过程线（图中实线）相比，考虑驳船升沉运动时的沉管运动响应与忽略驳船运动时的沉管运动响应相比，在运动幅值与相位上都发生较大的变化。在sway 方向和roll 方向，考虑驳船升沉运动时的沉管运动响应的历时过程线没有变化，表明驳船升沉运动对沉管在sway 和roll 方向的运动影响很小。

图4 驳船做升沉运动与忽略驳船运动情形的沉管运动响应（b=0.3 m）Fig.4 Motion response of tunnel element with and without barge heave motion（b=0.3 m）

为进一步考察驳船升沉运动相位差的影响，图5 给出了驳船升沉运动幅值为0.3 m、驳船运动与波浪之间的相位差分别取-π/2，-π/5，+π/5 和+π/2 情形的沉管升沉运动过程线。图中实线为考虑波浪作用与驳船升沉运动共同影响的沉管升沉运动时间过程线，虚线为忽略驳船升沉运动仅受波浪影响的沉管升沉运动时间过程线。为便于讨论，驳船升沉运动的时间过程线也在图5 中给出（图中的点划线）。由图5 可见，当驳船升沉运动的相位为(-π/2)时，沉管升沉方向的运动幅值最大约为0.4 m，此情形下驳船升沉方向运动的相位与忽略驳船运动时的沉管升沉方向运动的相位一致，沉管升沉方向的运动幅值为驳船升沉运动幅值（0.3 m）与忽略驳船运动时的沉管升沉方向运动幅值（0.1 m）之和；当驳船升沉运动的相位为π/2 时，沉管运动幅值最小约为0.2 m，此情形下驳船升沉方向运动的相位与忽略驳船运动时的沉管升沉方向运动相位刚好相反，沉管升沉方向的运动幅值为驳船升沉幅值与忽略驳船运动时的沉管升沉方向运动幅值之差。

图5 驳船升沉运动相位不同情况下沉管升沉运动过程线（b=0.3 m）Fig.5 Time history of tunnel element in heave motion under barge heave motion with different phases（b=0.3 m）

图6 是驳船升沉运动振幅b=0.1～0.5 m、相位θ=-π/2～π/2 情形对应的沉管升沉运动幅值（H=1.0 m，T=5 s）。

由图6 可见，当驳船升沉运动的相位θ 一定时，沉管运动幅值随着驳船升沉运动的振幅增加而相应增加。驳船升沉运动的相位θ=-π/2 时，对不同振幅的驳船升沉运动，沉管升沉方向的运动幅值最大值为驳船升沉运动幅值与忽略驳船运动时沉管升沉运动幅值之和，发生在驳船升沉运动相位与忽略驳船运动时沉管升沉方向运动的相位一致的情形。驳船升沉运动的相位θ=π/2 时，对不同振幅的驳船升沉运动，沉管升沉方向的运动幅值最小值为驳船升沉运动幅值与忽略驳船运动时沉管升沉运动幅值之差，发生在驳船升沉运动相位与忽略驳船运动时沉管升沉方向运动的相位刚好相反的情形。

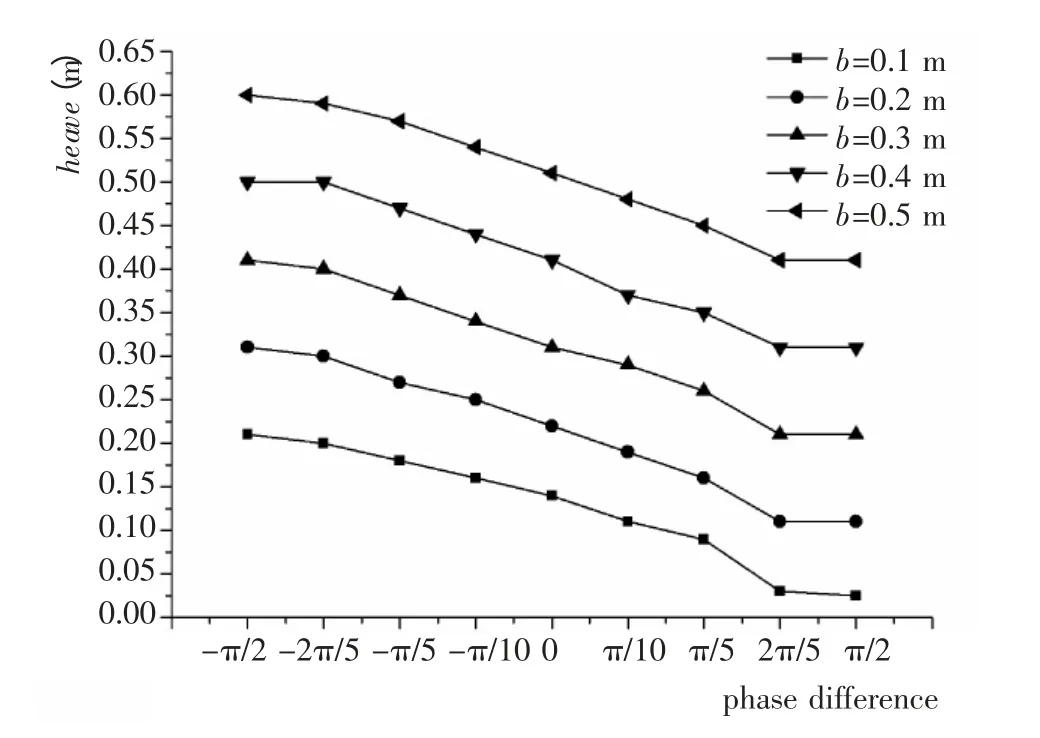
图6 驳船做不同升沉运动情况下的沉管升沉运动幅值（H=1.0 m，T=5 s）Fig.6 Movement amplitude of tunnel element in heave motion under barge with heave motion（H=1.0 m，T=5 s）

4 结论

本文考虑驳船升沉运动与波浪的共同作用，建立了时域求解沉管运动的数学模型，分析驳船做不同振幅与不同相位的升沉运动对沉管运动特性的影响规律，得到如下主要结论：

（1）与忽略驳船升沉运动时的沉管运动相比，驳船升沉运动振幅与相位对沉管升沉运动有较大的影响。当驳船升沉运动的相位θ 一定时，沉管运动幅值随着驳船升沉运动的振幅增加而相应增加。

（2）沉管升沉方向的运动幅值最大值为驳船升沉运动幅值与忽略驳船运动时沉管升沉运动幅值之和，发生在驳船升沉运动相位与忽略驳船运动时沉管升沉方向运动的相位一致的情形。沉管升沉方向的运动幅值最小值为驳船升沉运动幅值与忽略驳船运动时沉管升沉运动幅值之差，发生在驳船升沉运动相位与忽略驳船运动时沉管升沉方向运动的相位刚好相反的情形。

（3）在实际工程中采用驳船沉放法进行沉管管段沉放施工作业中，可通过改变驳船升沉运动的相位来减小沉管管段升沉运动。本文的研究工作是在假定驳船做已知的升沉运动的情形下进行的，实际上驳船运动和沉管运动需要在波浪场内耦合求解，该问题有待于进一步的研究。

［1］ZHAN D X，WANG X Q. Experiments of hydrodynamics and stability of immersed tube tunnel on transportation and immersing［J］. Journal of Hydrodynamics：Ser. B，2001（2）:121-126.

［2］Jensen O P，Olsen T H，Kim C W，et al. Construction of immersed tunnel in off-shore wave conditions Busan-Geoje project South Korea［J］. Tunneling and Underground Space Technology，2006，21:333.

［3］陈智杰.波浪作用下沉管管段沉放运动的试验与数值研究［D］.大连:大连理工大学，2009.

［4］Hess J L，Smith A M O. Calculation of non-lifting potential flow about arbitrary three-dimensional bodies［J］. Journal of Ship Research，1964，8（2）:22-44.

［5］GARRISON C J. Hydrodynamics loading of large offshore structures: Three-dimensional source distribution method［C］//ZIENKIEWICZ O C，LEWIS R W，STAGG K G W. Numerical Methods in Offshore Engineering. Chichester：wiley，1978:87-140.

［6］Liu Y H，Kim C H，Lu X S. Comparison of higher-order boundary element and constant panel methods for hydrodynamic loading［J］. International Journal Offshore and Polar Engineering，1991，1（1）:8-17.

［7］Teng B，Eatock Taylor R. New higher-order boundary element methods for wave diffraction/radiation［J］. Applied Ocean Research，1995，17（2）:71-77.

［8］Wehausen J V，Laitone E V. Surface waves［M］. Berlin: Springer-Verlag，1960：446-778.

［9］Stoker J J. Water Waves，Pure and applied mathematics［M］. New York: Inter science Publishers，Inc.，1957.