地铁车站纵梁内力研究
2013-08-28杨海
杨 海
(中铁隧道勘测设计院有限公司,天津 300133)
0 引言
近年来,随着地铁建设的快速发展,全国大多数省会城市及沿海地区经济较发达的城市均已投入到地铁建设当中,并且越来越多的城市有修建地铁的计划。据粗略统计,全国在建地铁的城市已超过30个。鉴于设计单位前期设计经验的积累和当前设计行业竞争愈趋激烈,如何在不影响工程质量的前提下降低工程成本成为当前提高设计水平的一项紧迫任务。在这种情况下,对结构设计的进一步优化和精细化提出了更高的要求。
针对地铁车站板和侧墙的优化设计,已有学者进行深入探究,如杨建学[1]、代坤[2]等均通过二维简化与三维实体计算对比分析,找出二维计算中存在的一些不足和尚需改进的地方。由于二维计算中存在一些不合理的简化,且无法按板梁协同受力分析,导致顶板及侧墙内力在二维计算与三维计算时有较大差异。因为实际工程中纵梁与板协同受力,所以引起地铁车站内力计算差异的主要因素为纵梁。当前对纵梁这一主要受力构件的研究还较少,尤其是采用传统分析方法与三维分析方法的对比分析更鲜有研究,故本文将针对车站纵梁的受力进行探索、研究。因中纵梁和底纵梁与顶纵梁受力力学模型类似,故本文仅对顶纵梁的受力进行研究,以期为类似工程的设计提供一些参考。
1 计算模型
以单柱双跨、双柱三跨这2种典型形式的地铁车站顶纵梁为分析研究对象,其结构平面布置见图1和图2。
图1以某2层地下单柱双跨车站的标准段作为分析实例,顶板覆土3 m,顶板厚800 mm(h0),侧墙厚700 mm,侧墙间净间距18.3 m,顶纵梁截面尺寸为1 200 mm×1 800 mm(b×h),柱截面尺寸为1 000 mm×800 mm,柱中心距8.0 m。除柱采用C50混凝土外,其余结构构件均采用C35混凝土。
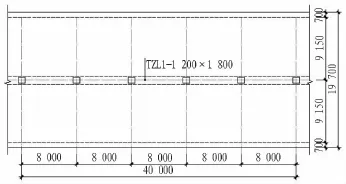
图1 单柱双跨车站顶纵梁结构平面布置图(单位:mm)Fig.1 Plan layout of structure of longitudinal beam of singlecolumn two-span Metro station(mm)
图2以某地下2层双柱三跨车站的标准段作为分析实例,顶板覆土3 m,顶板厚800 mm(h0),侧墙厚700 mm,侧墙间净间距21.3 m,顶纵梁截面尺寸为1 000 mm×1 800 mm(b×h),柱截面尺寸为1 000 mm×7 00 mm,柱中心距8.5 m,两顶纵梁中心线间距6.0 m。除柱采用C50混凝土外,其余结构构件均采用C35混凝土。

图2 双柱三跨车站顶纵梁结构平面布置图(单位:mm)Fig.2 Plan layout of structure of longitudinal beam of two-column triple-span Metro station(mm)
2 传统方法分析
2.1 单柱双跨站
在分析顶纵梁受力的时候,传统方法是将顶板上部水土荷载及自重、超载等按板面荷载按照板净宽的一半分担到顶纵梁上,取1延米为荷载统计长度,计算荷载统计结果见表1。

表1 计算荷载统计表Table 1 Loads calculated kN/m
2.1.1 荷载设计值
根据文献[3-6]的规定,按结构在施工阶段和使用阶段可能出现的最不利情况进行荷载组合。各种荷载组合及分项系数见表2。
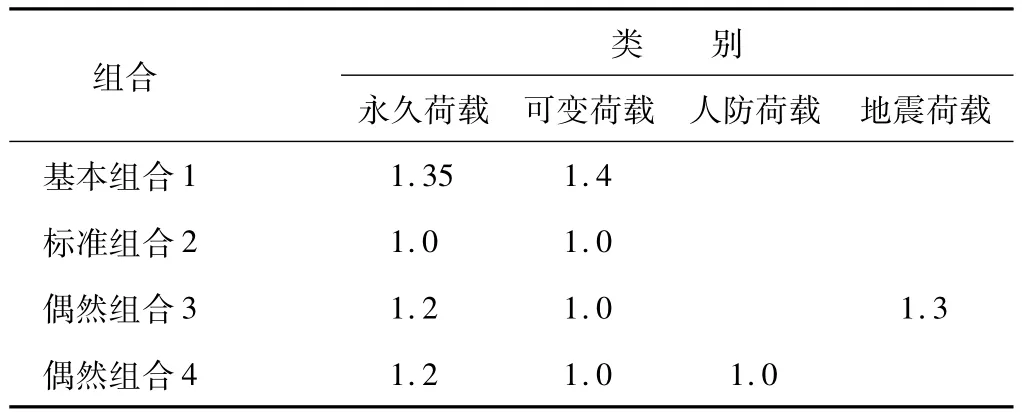
表2 荷载组合表Table 2 Load combination mode
基本组合考虑结构重要性系数1.1,人防荷载按6级人防抗力等级考虑,根据经验和理论计算,偶然组合3,4不控制结构设计。以下分别计算基本组合1(承载能力极限状态)和标准组合2(正常使用极限状态)时的结构内力。
1)承载能力极限状态时的荷载设计值

2)正常使用极限状态时的荷载设计值
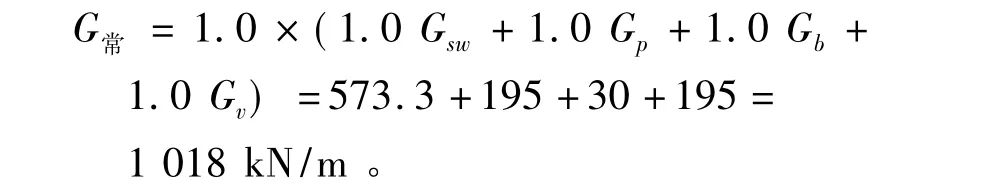
2.1.2 内力计算
1)顶纵梁取5跨,经计算承载力极限状态下的内力图(选取中间3跨)见图3和图4。

图3 顶纵梁弯矩图(单位:kN·m)Fig.3 Bending moment of longitudinal beam(kN·m)

图4 顶纵梁剪力图(单位:kN)Fig.4 Shear force of longitudinal beam(kN)
2)顶纵梁取5跨,经计算正常使用状态下的内力图(选取中间3跨)见图5和图6。
2.2 双柱三跨站
计算方法和原则同单柱双跨站,计算荷载统计结果见表3。
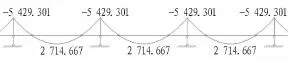
图5 顶纵梁弯矩图(单位:kN·m)Fig.5 Bending moment of longitudinal beam(kN·m)

图6 顶纵梁剪力图(单位:kN)Fig.6 Shear force of longitudinal beam(kN)

表3 计算荷载统计表Table 3 Loads calculated kN/m
2.2.1 荷载设计值
1)承载能力极限状态时的荷载设计值

2)正常使用极限状态时的荷载设计值
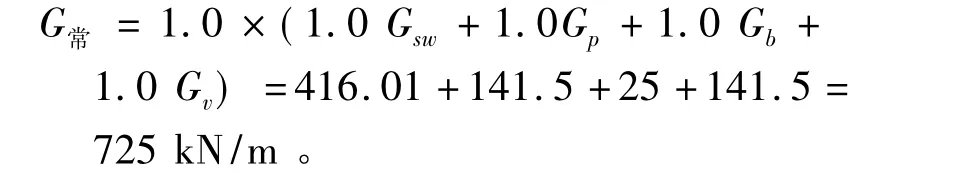
2.2.2 内力计算
1)顶纵梁取5跨,经计算承载力极限状态下的内力图(选取中间3跨)见图7和图8。

图7 顶纵梁弯矩图(单位:kN·m)Fig.7 Bending moment of longitudinal beam(kN·m)

图8 顶纵梁剪力图(单位:kN)Fig.8 Shear force of longitudinal beam(kN)
2)顶纵梁取5跨,经计算正常使用状态下的内力图(选取中间3跨)见图9和图10。

图9 顶纵梁弯矩图(单位:kN·m)Fig.9 Bending moment of longitudinal beam(kN·m)

图10 顶纵梁剪力图(单位:kN)Fig.10 Shear force of longitudinal beam(kN)
3 三维有限元分析
3.1 单柱双跨站
相比传统二维拆解、等效、忽略顶板本身刚度影响等分析方法,三维有限元分析方法更直接,也更接近实际情况。现以SAP2000通用有限元分析程序建立三维整体受力模型,顶板与侧墙采用薄板单元,纵梁及柱采用杆件单元,顶板与侧墙和纵梁之间刚性连接,顶板纵向两端为自由,顶板以0.5 m×0.5 m来划分网格,分析顶纵梁在构件协同受力状态下的内力大小。由于本例只分析顶纵梁受力,所以仅取下部为固定支座的车站负一层三维结构来作为受力分析模型,见图11。

图11 三维结构计算实体图Fig.11 3D structure calculation model
1)极限承载力状态下顶纵梁的内力图(选取中间3跨)见图12和图13。
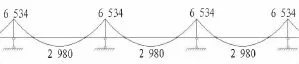
图12 顶纵梁弯矩图(单位:kN·m)Fig.12 Bending moment of longitudinal beam(kN·m)
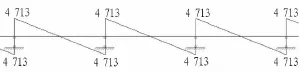
图13 顶纵梁剪力图(单位:kN)Fig.13 Shear force of longitudinal beam(kN)
2)正常使用状态下顶纵梁的内力图(选取中间3跨)见图14和图15。

图14 顶纵梁弯矩图(单位:kN·m)Fig.14 Bending moment of longitudinal beam(kN·m)

图15 顶纵梁剪力图(单位:kN)Fig.15 Shear force of longitudinal beam(kN)
3.2 双柱三跨站
双柱三跨站三维结构计算实体图见图16。
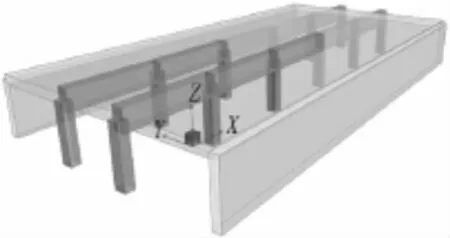
图16 三维结构计算实体图Fig.16 3D structure calculation model
1)极限承载力状态下顶纵梁的内力图(选取中间3跨)见图17和图18。

图17 顶纵梁弯矩图(单位:kN·m)Fig.17 Bending moment of longitudinal beam(kN·m)

图18 顶纵梁剪力图(单位:kN)Fig.18 Shear force of longitudinal beam(kN)
2)正常使用状态下顶纵梁的内力图(选取中间3跨)见图19和图20。

图19 顶纵梁弯矩图(单位:kN·m)Fig.19 Bending moment of longitudinal beam(kN·m)
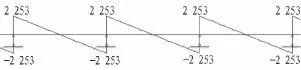
图20 顶纵梁剪力图(单位:kN)Fig.20 Shear force of longitudinal beam(kN)
4 对比分析
4.1 单柱双跨站
根据统计结果,对比传统方法 (简称二维)与三维有限元整体分析方法 (简称三维)的内力计算结果差异。
4.1.1 端部内力差异
1)弯矩差异(见表4)。

表4 弯矩对比表Table 4 Comparison of bending moment kN·m
2)剪力差异(见表5)。
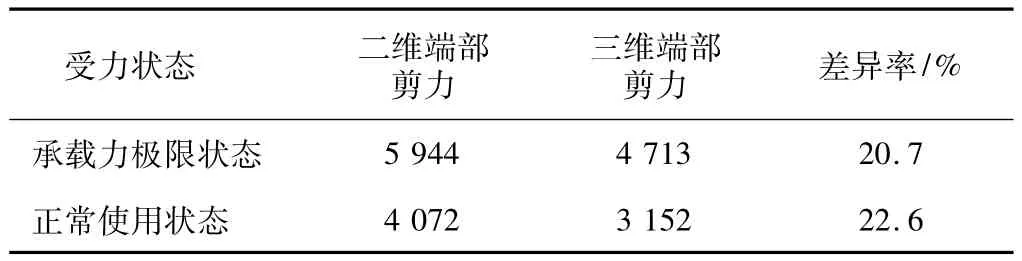
表5 剪力对比表Table 5 Comparison of shear force kN
4.1.2 跨中内力差异
1)弯矩差异(见表6)。

表6 弯矩对比表Table 6 Comparison of bending moment kN·m
2)跨中剪力均为零。
4.1.3 差异规律
1)二维计算内力结果均大于三维计算结果。
2)对于端部弯矩,二维比三维计算结果多15% ~20%。3)对于跨中弯矩,二维比三维计算结果多25%左右。4)剪力大小差异在20%左右,按6肢箍来计算配置箍筋,相差约1个箍筋直径大小等级。
5)结构所受荷载大小增减与弯矩、剪力差异百分比均成反向变化关系。即结构所受荷载越大,弯矩、剪力差异越小;反之则差异越大。
4.2 双柱三跨站
根据统计结果,对比传统方法(简称二维)与三维有限元整体分析方法(简称三维)的内力计算结果差异。
4.2.1 端部内力差异
1)弯矩差异(见表7)。

表7 弯矩对比表Table 7 Comparison of bending moment kN·m
2)剪力差异(见表8)。

表8 剪力对比表Table 8 Comparison of shear force kN
4.2.2 跨中内力差异
1)弯矩差异(见表9)。

表9 弯矩对比表Table 9 Comparison of bending moment kN·m
2)跨中剪力均为零。
4.2.3 差异规律
1)二维计算内力结果均大于三维计算结果。
2)对于端部弯矩,二维比三维计算结果多25%左右。
3)对于跨中弯矩,二维比三维计算结果多30%左右。
4)剪力大小差异在27%左右,按6肢箍来计算配置箍筋,相差约1个箍筋直径大小等级。
5)结构所受荷载大小增减对弯矩、剪力差异百分比变化率影响不明显。
5 结论与建议
因地铁车站各纵梁结构受力力学模型相似,故通过对顶纵梁的分析,可知底纵梁、中纵梁与顶纵梁有同样或类似的结论。
1)不论单柱双跨还是双柱三跨典型车站的纵梁内力大小,传统分析方法与三维有限元分析方法之间的差异具有相似的规律。
2)传统方法分析的内力均大于三维有限元分析的内力。
3)根据前面荷载变化与计算差异率的规律可知,单柱双跨车站纵梁的计算差异对覆土厚度较敏感;双柱三跨车站纵梁的计算差异对覆土厚度不敏感。
4)对于端部弯矩,二维计算比三维计算大15% ~25%。
5)对于跨中弯矩,二维计算比三维计算大25% ~35%。
6)对于支座剪力,二维计算比三维计算大20% ~30%。
产生这种差异的根本原因在于二维计算中无法分析板梁协同受力的空间作用,而三维计算则能分析板梁协同受力的空间作用,所以三维计算结果与结构实际受力更接近。
与三维有限元计算方法相比,传统计算方法较快捷,并且计算结果也能基本满足工程设计需要,但是其合理性和精细化程度有待提高。为了提高结构设计质量,在沿用传统方法计算时,结合工程实际经验,建议对宽度在19.7 ~22.7 m、柱跨在 8.0 ~8.5 m 的浅埋地铁车站的二维计算结果进行适当调整。
折减后的二维计算结果更接近结构实际受力状况,减少了工程中不必要的浪费。在以后的设计中,最好采用三维计算。建议下一步可对不同板跨、不同柱距和不同覆土条件下的纵梁受力进行全面、深入的研究。
[1] 杨建学.明挖地铁车站不同计算方法计算结果比较[J].甘肃科技,2009(13):133-136.
[2] 代坤.明挖地铁车站空间计算模型与平面计算模型的对比分析[J].隧道建设,2010,30(S1):254-258.(DAI Kun.Comparative analysis on 3D cmputation model and 1D cmputation model for Metro sations constructed by cut and cover method [J].Tunnel Construction,2010,30(S1):254-258.(in Chinese))
[3] 中国建筑科学研究院.GB 0009—2012建筑结构荷载规范[S].北京:中国建筑工业出版社,2012:9-12.
[4] 中国建筑科学研究院.GB 50011—2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010:31-43.
[5] 中国建筑设计研究院.GB 50038—2005人民防空地下室设计规范[S].北京:中国建筑工业出版社,2005:88-107.
[6] 北京城建设计研究总院.GB 50157—2003地铁设计规范[S].北京:中国计划出版社,2003.
[7] 中国建筑科学研究院.GB 50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
