基于粗集—支持向量机模型工程项目风险评价研究①
2013-08-28潘洪浩蔡璟珞
潘洪浩 蔡璟珞
(1.中国海外工程有限责任公司,北京 100048;2.华北科技学院学生工作处,北京 东燕郊 101601)
0 引言
由于工程项目规模越来越大,技术、工艺也日趋复杂,故各种风险也日益增多,而且原因错综复杂,因此工程项目所蕴含的风险必须进行提前估计和预测,而其风险管理水平是其风险控制成功与否的关键因素,其中风险分析与评价又是风险管理过程中的重要环节[1]。传统的风险评价方法主要是运用单一方法进行风险评价,此方法已很难准确、科学地评价复杂多变的工程项目风险因素[2]。本文通过对项目风险的分析与评估,将工程项目风险因素指标分为社会风险、经济风险、技术风险、自然风险及管理风险等五大类,以此为基础,同时提出了采用粗集[3-5]对其相关指标进行约简,而后运用具有人工智能性的支持向量机[6]分类方法对其进行评价,提高了工程项目风险评价的准确性和科学性,旨在于寻求度量工程项目风险的有效方法,为项目风险管理提供新的思路。
1 工程项目风险因素特征分析
风险一般指由于在从事某项特定活动过程中存在的不确定性而产生的经济或财务损失,自然破坏或损伤的可能性。任何的工程项目中都存在风险,风险会造成工程项目实施的失控现象,如工期增长、成本增加、计划修改等等,这些都会造成经济效益的降低,甚至整个工程项目的失败[7]。
可以知道,众多内外部各种因素构成了工程项目的风险,把这些能导致风险发生变化的各种因素称之为风险因素,工程项目风险因素一般都具有如下特征:一是风险递增性。主要是指随着工程项目进度的进行,工程项目的累积投入会越来越大,其可能的风险损失也会随之递增,而且这种风险损失的递增是不可避免了。此外,假如在某个阶段错误地中止可行的项目,其所造成的决策风险损失不仅包含前期的累积投入,还包括因中止项目导致的机会损失[8,9]。二是风险传递性。主要是指在工程项目的n个阶段中,每一个阶段的风险因素都会对后续阶段产生影响。三是随机性与突变性,风险因素的出现以及其相互之间的影响具有一定的随机性。四是风险可变性。工程项目风险发生概率和损失随着项目建设在不断地动态变化,每一阶段其风险都有可能是不同的,即使同一风险在不同阶段发生概率和损失也是不同的。五是主观影响性。因此,风险因素的判定,需要尽可能量化风险因素指标,以剔除主观不确定因素,提高决策的科学性。
2 工程项目投资指标的确定
工程项目投资作为集专业性、技术性、管理性极强的活动,鉴于其自身所具有的政策限制性、位置固定性、范围特定性等特点,既可以给予投资者较高收益,也蕴藏着一定地风险,还是一个高风险、高投入和高回报的产业。
本文通过对诸多实际投资项目调研分析的基础上,有丰富实践经验的专家咨询,并参考前人的研究资料的前提下,建立起一套较为科学、合理、完整、可靠的工程项目风险评价指标体系,采用粗集理论对这一完整指标体系进行约简,获得影响工程项目风险的主要因素,再利用层次分析法重新确定各指标的权重,具体如表1。

表1 工程项目投资风险指标及其权重
3 粗集理论
粗集(RoughSet)理论是由波兰学者Z.Pawlak在1982年提出的,粗集理论处理数据的基本思路:对于需处理的数据,在一定的分类规则或决策规则前提下,通过粗集理论进行约简,约去冗余指标,获得主要影响指标或因素,是极为有效和科学的模糊数据处理工具[10]。
3.1 信息系统
一个信息系统 S可表示为:S=(U,A,V,f);其中 U 为论域,(U={x1,x2,…,xn})由有限个研究对象组成;A=C∪D为属性集,其中C为条件属性集,D为决策属性集;V为值域;f为映射,对∀a∈A,x∈U,实现关于属性 a的值。
3.2 不可区分关系
粗集理论认为知识是与分类紧密联系在一起的,分类的过程就是将相差不大的对象分为一类,它们的关系就是不可分辨关系也称等价关系。知识库可表示为K=(U,R)。其中U为非空有限集称为论域,R是U上的一族等价关系。UΠR为R的所有等价类族。
3.3 属性约简与核
定义1 假定S=(U,R)为信息系统,R是U上的等价关系族,r∈R,若U/IND(R)=U/IND(R -r),则称R是R中可被约简知识,否则,称R是R不可约知识。
定义2 如果任一r∈P(P⊆R),均为P不可约去的,则称等价关系族P是独立的,否则P是相关的。
定义3 设S=(U,R)为信息系统,若子族P⊆R满足IND(P)=IND(R),且P是独立的,则称P是R的一个约简。
定义4 设S=(U,R)为信息系统,R中不可约去的属性,称做R的核属性,所有核属性构成的集合称为核集,记作Core(R),称Core(R)为R的核。
3.4 粗集的上、下近似及边界
定义3 称BNR(X)=为X的R边界域,称NEGR(X)=U-为X的负域。显见,负域中的元素由不能确定是否属于X的元素组成。
3.5 决策表的简化
决策表的简化就是化简决策表中的条件属性,化简后的决策表具有与化简前的决策表相同的功能,但是化简后的决策表具有更少的条件属性。因此,决策表的简化在实际应用中相当重要,同样的决策可以基于更少量的条件,使我们通过一些简单的手段就能获得同样要求的结果。决策表的简化步骤如下:
1)进行约简,在不改变决策前提约简掉冗余列;
2)约简掉重复行;
3)消去属性的冗余值。
本文主要应用这些步骤进行属性约简,以找到影响工程项目风险的主要指标,约简掉冗余的指标,以利于下一步的工程项目风险评价。
4 基于支持向量机的回归模型
利用支持向量机(Support Vector Machines,简称SVM)分类的基本思想对工程项目风险进行评价。
假设训练样本为{(x1,y1),…(xi,yi)},其中xi∈Rm是第i个学习样本的输入值,且为m维列向量,yi∈R为对应的目标值。采用一个非线性映射φ(x)将样本从原空间映射到维数为k(k可能是无穷大)的高维特征空间F中,然后在高维特征空间中进行线性回归[3,6,7]。
设回归函数为:
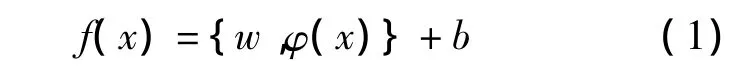
式中,(,)表示内积;为权向量,w∈Rk为描述函数f(x)复杂度的项;Rm空间到F空间的非线性映射;b为常数,b∈R。
将上述函数回归问题等价于最小化代价泛函:
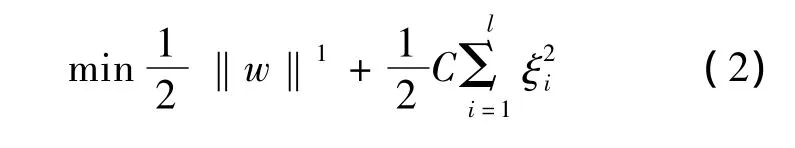
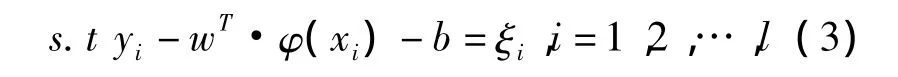
式中,ξ为松弛变量,ξ≥0;C为惩罚参数,C>0,它的作用是在经验风险和模型复杂度之间取一折中。
为了求解上述优化问题,建立Lagrange函数:
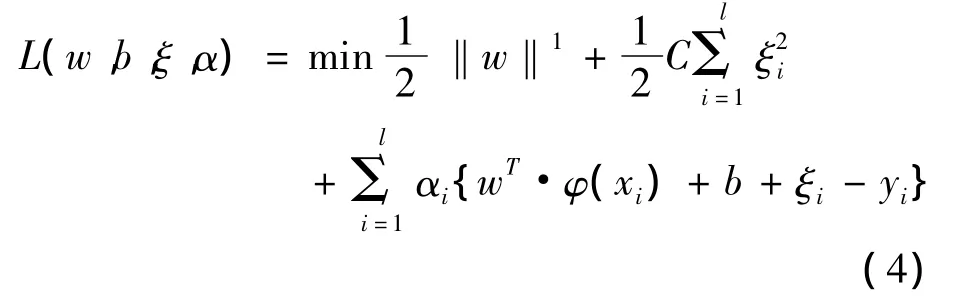
式中,αi为Lagrange乘子。

式中,K(x,xi)为一个满足Mercer条件的核函数。该函数可在不知非线性变换的具体形式下实现算法的非线性化,这是支持向量机的一个显著特点。其中如下所示的径向基(RBF)核函数是非常常用的一种核函数:
径向基核:
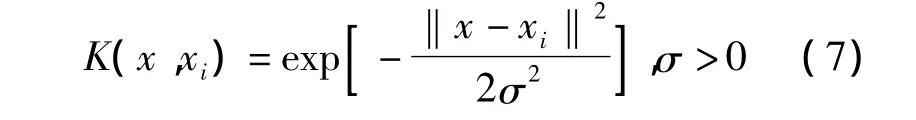
支持向量机回归模型只需根据优化准则选择输入节点数m和相关参数,训练结构由支持向量数(隐层节点数)自动决定,连接权由算法自动获得,而且其松弛变量使其具备良好地泛化能力,故优于神经网络分类模型。
5 实证分析
该文引用项目,占地面积为67hm2,建成后用于商业及住宅,五所高校与之毗邻,周围还有两个医院,地理位置优越,绿化率较高。由于该项目开发规模较大,周期长,投资额大。所以,面临风险较大,故要求开发企业做出合理风险评价和预测,以期做好风险的防范及控制。
据此开发企业的经验及相关专家的评价,对于本项目所选取的指标进行粗集约简,再对约简后的指标重新确定权重,具体如表2。在这一指标体系下,选取8个地产工程项目的有关数据作为学习样本,并邀请相关专家对前7个项目按照本文的指标体系进行支持向量机进行分类风险评价,获得训练样本和检验样本(具体思路为:前五个为训练样本,后两个为检测样本),具体如表3。
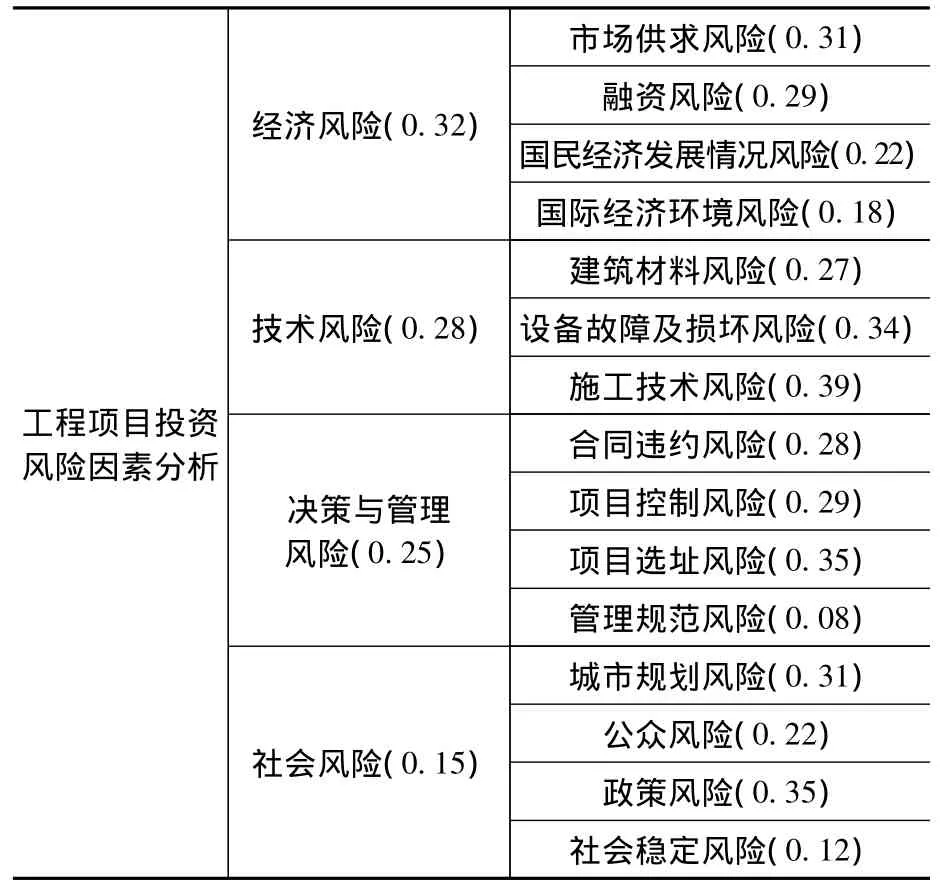
表2 约简后工程项目投资风险指标及其权重

表3 支持向量机模型的训练及检测样本
通过对于样本进行支持向量机训练,直到满足预设误差后,停止学习,获得支持向量机分类模型,此时相关参数,如惩罚系数、松弛变量等也一一确定。设定的学习率为0.02,误差为:0.00009。
再通过此模型对上述五个样本进行支持向量机分类,得到训练样本输出结果,具体见表4,检测样本输出见表5。
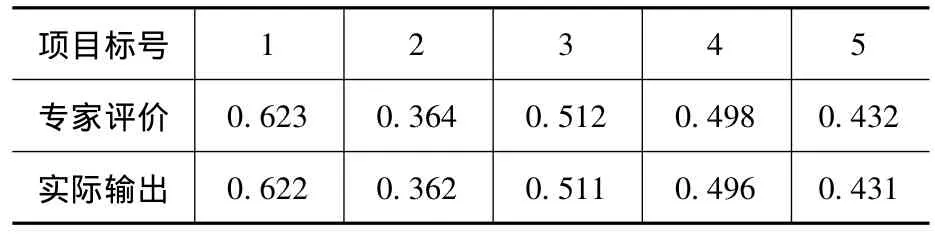
表4 支持向量机模型训练样本输出
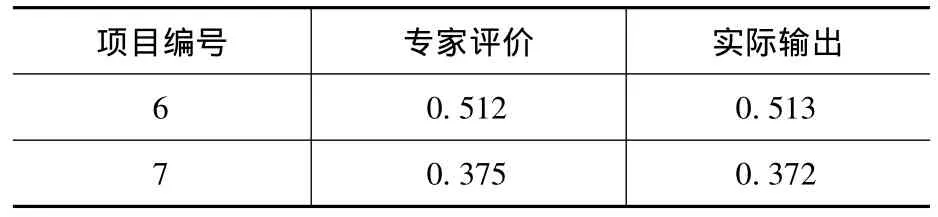
表5 支持向量机模型检测样本输出
检测样本网络输出结果与专家评价结果基本相符合,误差为0.000 03324,满足设定要求。工程项目风险评价模型业已建立,可利用此模型对工程项目投资风险进行风险评价,以作为项目决策者的决策依据。
通过以上的以往数据分析,把该项目经过调研的有关数据进行整理(见表6),将表6的数值作为支持向量机模型的输入值,运用已经训练好支持向量机分类模型进行分类评价,得出最终风险数值为0.613,说明该项目存在一定的风险。随着项目的展开,需对项目做出长期动态的风险评价与控制,作好风险的防范与预防工作。

表6 该项目各指标相关值
6 结论
通过本文研究表明:
1)粗集与支持向量机模型相结合的方法可以较好地解决支持向量机自学习的高质量训练样本数据获得问题,使支持向量机模型理论在工程项目风险的评价中的应用得到进一步加强。
2)构建了工程项目风险的评价指标体系,并运用粗集理论和利用支持向量机模型对指标进行约简和评价,建构了工程项目风险评价模型,为工程项目风险评价提供了新方法。
[1] M ILLER R ,LESSARD D.The Strategic Management of Large Engineering Projects[M].Cambridge,MA:The M IT Press,2000:21 -23
[2] 西宝,李一军.复杂工程风险管理的信息密度演化计算方法[J].哈尔滨工业大学学报,2005,(1):56 -59
[3] 席一凡,聂兴信,王超.工程项目风险评价模型研究[J].灾害学,2009,(3):89-92
[4] 曹庆奎,任向阳,刘琛,刘历波.基于粗集-未确知测度模型的企业技术创新能力评价研究[J]. 系统工程理论与实践,2006,9(4):67-72
[5] 张文修,吴伟志.粗糙集理论与方法[M].北京:科学出版社,2003
[6] 苏怀智,温志萍,吴中如.基于SVM理论的大坝安全预警模型研究[J].应用基础与工程科学学报,2009,17(1):40 -47
[7] 王卓甫.工程项目风险管理理论方法与应用[M].北京:中国水利水电出版社,2003
[8] 钟登华,张建设,曹广晶.基于AHP的工程项目风险分析方法[J].天津大学学报,2002,35(2):162-166
[9] 王连芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990:66-87
[10] 程乾生.层次分析法AHP和属性层次分析模型AHM[J].系统工程理论与实践,1997,(11).56 -59
