用于迷宫电脑鼠的一种迷宫补全算法
2013-08-27于佳维潘志雄马忠梅
于佳维,潘志雄,马忠梅
(北京理工大学 计算机学院,北京100081)
引 言
“电脑鼠(MicroMouse)”是一种使用嵌入式微控制器、避障传感器和机电运动部件构成的一种智能行走机器人。其主要功能为在迷宫中行走,并通过传感器收集迷宫中的环境数据,通过对数据的分析和运算找到通往目的点的路径。国际电工和电子工程学会每年都要举办一次国际性的电脑鼠走迷宫大赛,我国从2009年开始举办全国性的电脑鼠走迷宫大赛。比赛的关键在于如何在迷宫中快速找到合适路线并且到达目标点。目前对电脑鼠的改进有3个主要的研究方向:硬件上电脑鼠性能的改进、搜索算法上的改进和比赛策略上的改进。本文基于电脑鼠走迷宫大赛的规则介绍了搜索算法改进的一种思想。
1 电脑鼠走迷宫的规则介绍
因为本文的算法基于电脑鼠走迷宫竞赛,为了方便阐述,现简要介绍电脑鼠走迷宫的竞赛规则。
1.1 迷宫的规范
电脑鼠比赛用的标准迷宫由16×16个18cm×18cm的正方形单元所组成。迷宫的隔墙高5cm,厚1.2cm,两个隔墙所构成的通道的实际距离为16.8cm。外墙将整个迷宫封闭。迷宫的起始单元可选设在迷宫4个角落之中的任何一个。起始单元必须3 面有隔墙,只留一个出口。例如,如果没有隔墙的出口端为“北”时,那么迷宫的外墙就构成位于“西”和“南”的隔墙。电脑鼠竞赛的终点设在迷宫中央,由4个正方形单元构成。在每个单元的4角可以插上一个小立柱,其截面为正方形。立柱长1.2 cm,宽1.2cm,高5cm。小立柱所处的位置称为“格点”。除了终点区域的格点外,每个格点至少要与一面隔墙相接触。电脑鼠迷宫图如图1所示。

图1 电脑鼠迷宫图
1.2 竞赛主要规则
电脑鼠的基本功能是从起点开始走到终点,这个过程称为一次“运行”,所花费的时间称为“运行时间”。从终点回到起点所花费的时间不计算在运行时间内。从电脑鼠的第一次激活到每次运行开始,这段期间所花费的时间称为“迷宫时间”。如果电脑鼠在比赛时需要手动辅助,这个动作称为“碰触”。竞赛使用这3个参数,从速度﹑求解迷宫的效率和电脑鼠的可靠性3个方面来进行评分。
电脑鼠的得分是通过计算每次运行的“排障时间”来衡量的,排障时间越短越好。排障时间是这样计算的:先将迷宫时间的1/30加上一次运行时间,如果这次运行结束以后电脑鼠没有被碰触过,那么还要再减去10s的奖励时间,得到的就是排障时间。每个电脑鼠允许运行多次,取其中最短的排障时间作为参赛的计分成绩。
例子:一个电脑鼠在迷宫中运行时间为4min(240s)没有碰触过,迷宫时间使用了20s,这次运行的排障时间就是:20s+(240s×1/30)-10s=18s。
2 算法概述
2.1 算法提出的背景
电脑鼠走迷宫进行迷宫搜索的最基础算法即为对迷宫进行全搜索,也就是将迷宫中的每一个格子都走遍。这种算法可以得知迷宫的全部信息,从而搜索出到达目的点的每一条路径,再通过一定的路径选择方法得出起点到终点的最短路径。但是按照上述的竞赛规则,显然对迷宫进行全搜索会使得迷宫时间过长。在特殊迷宫的情况下会使得迷宫时间远远高于预期,所以全搜索的搜索方法效率并不高,在现在的比赛中已经基本见不到。
所以,如何在最短的时间内快速地找到一条基本合适的路径就变得十分重要。而对于迷宫进行部分搜索,如何优化使得搜索时间尽量短,是解决上述问题的主要思考方向。下面就此问题提出一种算法。
2.2 算法思想
电脑鼠在起点处第一次运行时,对整个迷宫的信息都是未知的。电脑鼠通过在迷宫中行走来获取迷宫的情况。但是,传统的电脑鼠搜索算法往往只注重当前所在格的信息,而忽略了当前格子信息对周围格子的影响;注重通过小车行走来获得信息,而忽略了通过算法提前搜索分析行走的可行性。
以往的算法只注重当前格子的状态,比如电脑鼠所在格子状态为上面有墙,下面有墙,左侧无墙,右侧无墙。实际上探测到当前格子所能掌握的信息远比这多,比如在上面例子的基础之上还能推测出电脑鼠当前位置的上面一格的下面有墙,下面一格的上面有墙,左面一格的右侧无墙,右面一格的左侧无墙。
以往算法在一些格子的部分信息未知的情况下,选择让小车行走去获得信息,这样有可能陷入“死胡同”。实际上可以让算法去“行走”,即先用广度搜索算法预先搜索去分析可行性,再让小车行走。
本文提出的算法则利用了已获得的和补全的信息,从而推测出迷宫中只有一个入口的不规则形状死路。将这些死路在记录信息中进行“堵死”处理,从而避免了电脑鼠进入死路进行搜索,大大节省了搜索时间,提高了搜索效率。
3 “补全迷宫”算法
3.1 数据结构
采用一个字节的8位来表示一个迷宫格的信息,低4位从左到右分别代表“左”、“下”、“右”、“上”4个方向,1表示没墙,0表示有墙,方向相当于坐标的X 与Y 轴;而高4位与低4位的方向一一对应,1表示该方向搜索过,0为未搜索过。当高4位全为1时候,即当前格的4个方向都搜索过,表示当前格是小车已经走过的。该数据结构充分利用了字节的全部8位信息,减少了不必要的浪费。
例如:当一个字节为0100 0000 的时候,高4 位中“下”方向为1,表示当前格的“下”方向是搜索过的,即该方向的“墙”是已知的。这时低4位中对应位的数值才有意义,可以看出“下”方向为有墙。
在广度搜索时,采用队列数据结构存储有路的方格,不断取出队列的头一个方格进行分析,搜索到四周有路的方格加入队列,直到达到搜索目的。
3.2 核心算法
算法的核心是“信息补全”和“预先搜索”。
3.2.1 信息补全
当小车走到某一格的时候,不仅要更新当前格的全部“墙”信息,还要更新四周格子的部分“墙”信息。
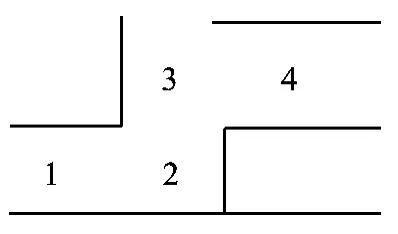
图2 电脑鼠迷宫信息补全图
电脑鼠迷宫信息补全图如图2所示,初始4格的位置信息都为00000000。当小车处在“1”方格中,根据小车自身探测结果可得该位置的信息为1111 1010,高4位为4个1,表示当前格周围4个方向都已经搜索过,此时低4 位对应的信息有效,分别表示“左”方向没墙,“下”方向有墙,“右”方向有路,“上”方向有墙。
经过信息补全,可以更新四周的格子的部分信息,如“2”。虽然“2”格小车还未走过,但是可以通过已经走过的“1”格知道“2”格的部分信息为1000 1000,高4位为1000,表示“2”格小车还未走过,但是“左”方向已经搜索过,为“左”方向没墙。而当小车走到“2”时,可知“上”方向有路,通过信息补全可得,“3”的“下”方向也有路。
通过信息补全的方法,可以减少小车的搜索,提高小车的搜索效率,为“预先搜索”提供信息的支持。
3.2.2 预先搜索
当小车处在某一格子的时候,4个方向中有路可走,不是直接让小车通过法则选择一条路前进,而是先让小车通过“预先搜索”算法判断往该方向前进是否有可能到达终点,如果没有可能到达终点,则不往该方向前进,将其“堵死”,封锁整个“死胡同”。
该方法利用之前小车搜索的信息以及补全的部分迷宫信息,其中将还未搜索过的方向全部假设为没墙,采取“广度搜索”策略,对从当前格某一方向到终点的路径进行搜索,获知该方向是否有可能到达终点,从而达到目的。而算法执行的时间要远小于小车行走时间,可忽略不计。
电脑鼠迷宫预先搜索图如图3所示,“1”为起点,“2”为终点,而“a”“b”“c”都是没必要走的“死胡同”,“3”“4”“5”为即将走入“死胡同”的前一格。可以看出,当小车在搜索时,要是进入这些“死胡同”,将做大量的无用功,在里面绕来绕去却无法通往终点,还需出来,浪费时间。
当小车搜索到“5”方格处时,有“左”和“上”两个方向可以选择,可以采取“预先搜索”的方法,对“左”方向进行分析,虽然“c”中的单元格小车还未搜索过,但是其四周的单元格都已经搜索过,根据四周方格搜索的信息对其补全,将未搜索的方向全部假设为没墙,可得“c”的补全图如图4所示,运用广度搜索方法分析判断,若往“左”方向进去,无论如何走,都到达不了终点,所以在“5”方格出的“左”方向是不可行的,继续用算法对其他有路的方向进行分析。
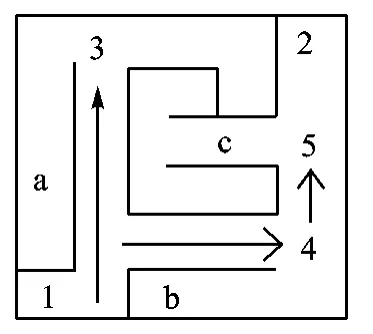
图3 电脑鼠迷宫预先搜索图
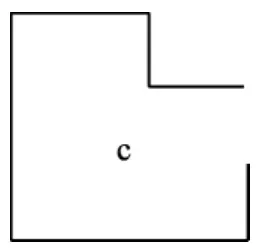
图4 电脑鼠迷宫“死胡同”补全图
“预先搜索”算法可以阻断“死胡同”这种耗费大量搜索时间的路径,减少了没必要的搜索,大量减少搜索量,提高竞赛成绩。
3.3 算法实现
3.3.1 信息补全算法
信息补全算法的程序流程图如图5所示。
用Car[16][16]数组存储每个方格的“墙”信息,初始化全部为00000000。小车每搜索到一格时,更新当前方格的信息,接着补全四周方格的信息。
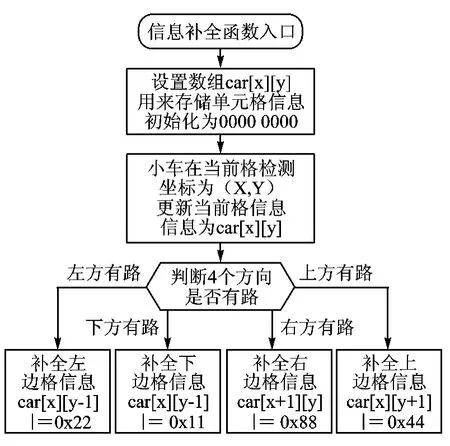
图5 信息补全程序流程图
对四周方格信息的补全,可直接采用位运算进行“与”“或”求得。低4位中1为没墙,0为有墙;高4位中1表示该方向搜索过,0为未搜索过。
其中核心代码实现:

3.3.2 预先搜索
预先搜索的程序流程如图6所示。
“预先”,即在小车行走前分析小车往某一有路方向前进的可行性;“搜索”,即采用广度搜索策略,对已有的搜索信息以及补全的信息进行分析,判断小车是否有可能从该方向到达终点。
广度搜索,即首先将根节点放入队列中,从队列中取出第一个节点,验证其是否为目标,在迷宫中搜索即为验证其是否为终点。如果是,则结束搜索并返回结果;否则将符合条件的子节点加入队列中,即将4个方向有路的节点加入队列中,重复取头节点,直到队列为空,返回分析结果。
由于一般微控制器的可用栈大小是有限制的,如果用深度搜索的话,在全迷宫中会造成栈溢出,所以采用动态队列,进行广度搜索。
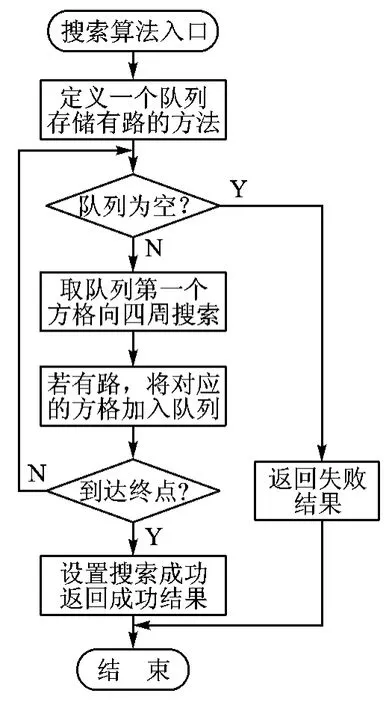
图6 预先搜索流程图
在广度搜索中,将那些未搜索的方向全部假设为没墙。核心代码如下:


结 语
本文介绍了一种迷宫电脑鼠在搜索过程中的优化算法。通过对搜索信息的扩展和分析达到对电脑鼠走迷宫过程中的无用路径进行删除,从而达到节省搜索时间、提高比赛成绩的目的。该算法已应用在2012年全国电脑鼠走迷宫大赛中,优化效果比较明显。在电脑鼠走迷宫竞赛的影响力日益扩大的今天,提供了一种在算法上对电脑鼠进行优化的思路。同时也欢迎大家对算法中的问题和可以改进的地方进行讨论,提出宝贵意见。
[1]Mark Allen Weiss.Data Structures and Algorithm Analysis in C[M].北京:人民邮电出版社,2005.
[2]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2007.
[3]广州致远电子有限公司.电脑鼠开发设计指南[OL].[2012-09].http://embedtools.com.
[4]张萌,和湘,姜斌.单片机应用系统开发综合实例[M].北京:清华大学出版社,2003.
[5]贺利军.智能老鼠走迷宫算法的设计[J].电脑与电信,2008(10):44- 45.
