反操纵大扭矩电动加载系统设计与应用
2013-08-26魏志强牛国臣张小磊
魏志强,牛国臣,张小磊
(北京航空航天大学机器人研究所,北京 100191)
0 引言
为满足新型舵机对正反操纵尤其是反操纵力矩加载测试的需求,必须设计性能稳定且可靠的模拟力矩加载系统,实现对舵机高精度反操纵模拟加载。根据实际需求,设计了大扭矩反操纵电动负载模拟系统,对提高新型舵机性能及有效评价提供了有力的技术保证。为抑制多余力矩,在分析系统构成及控制方法的基础上,提出多环级联嵌套的力/位置混合控制模式,基于舵机角度和力矩前馈补偿并采用PID参数自适应控制,获得了不同加载扭矩下的高精度、高对称度及高线性度的反操纵模拟负载系统,在实际平台上进行了加载实验,证明了所提方法的有效性,并满足了实际需要。
1 系统结构
反操纵电动负载系统采用带有编码器的大扭矩力矩电机,它具有工作转矩大、转矩波动小及可长时间工作在堵转状态等特点。反操纵力矩负载模拟系统组成如图1所示。
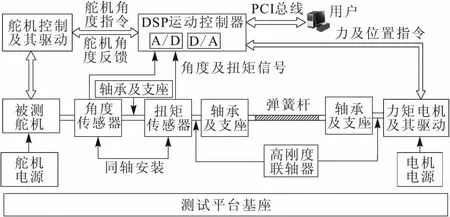
图1 反操纵力矩负载模拟系统
加载扭矩由高精度扭矩传感器检测,反馈到运动控制器中形成力矩闭环,以跟踪加载指令;被测舵机输出轴转角变化由高精度码盘测量,其与扭矩信号一起经A/D转换后存储到加载控制器中,从而根据检测扭矩值、舵机转角变化值计算出舵机实际所受反操纵力矩。系统中的弹簧杆作为力矩缓冲器,能有效抑制舵机位置扰动产生的高频干扰力矩,从而改善加载效果。
在此,结合参考文献[1]对正反操纵定义:舵机运行过程中,气动载荷对舵机轴产生的力矩方向与舵机轴运动方向一致时为反操纵加载,此时,舵机轴将在一定气动载荷作用下偏离平衡位置,舵偏角δ将不断加大;反之,气动载荷对舵机轴产生的力矩方向与舵机轴运动方向相反时为正操纵加载,此时,舵机轴将在一定气动载荷作用下回到平衡位置,舵偏角δ趋于零。
2 系统数学模型
2.1 系统模型分析
为便于模型分析做如下假设[2]:
a.整个传动轴系除弹簧杆外都为刚性联接。
b.采用大扭矩力矩电机,其本身转动惯量相对较高(0.3kg·m2),则将轴系等效转动惯量全部换算到电机轴惯量中。
另外,在加载模式中,将扭矩及角度传感器放置于被测舵机端,有利于准确测量舵机所受扭矩及角度变化值。
2.2 力矩电机及驱动模型
电机电压平衡方程与转矩平衡方程为[3-4]:

Um为力矩电机电枢电压;im为力矩电机电流;Rm为电机等效电阻;Lm为电机等效电感;KE为电机反电动势常数;θm为电机转角;Tm为电机输出转矩;Jm为电机轴转动惯量;Bm为电机的阻尼系数;TL为电机负载转矩。
驱动器放大环节可表示为:

ui为控制输入信号。
2.3 弹簧杆模型
忽略弹簧杆自身转动惯量及其扭矩传输的损耗,力矩电机与弹簧杆首端之间安装有高刚度弹性联轴器、扭矩传感器,其等效刚度远大于弹簧杆刚度,所以,可认为力矩电机与弹簧杆采用刚性联接。同理,弹簧杆末端与舵机轴也认为是刚性联接。因此,弹簧杆首末端角度变化与施加到舵机的力矩TL之间的关系为:

KL为弹簧杆刚度系数;θm为力矩电机转角;θa为舵机轴转角。
综上所述,对系统按两质量弹性系统进行动力学建模。同时,针对控制系统的目的是要精确跟踪力矩指令,与舵系统模型并无直接关系,舵控指令信号和舵机轴角位移都是引起多余力矩的一个物理量[3]。因此,不考虑舵机模型,从而也避免了控制系统阶次的提高,电机加载转矩关于电机控制输入和舵机轴转角之间的传递函数:

KT为电机扭矩常数。
3 弹簧杆刚度确定
弹簧杆刚度的大小对系统控制性能有一定的影响,刚度系数小,则系统动态响应缓慢,系统频带减少;而刚度系数过大,会导致系统稳定性下降,使系统控制及多余力矩消除难度增大[5]。为了保证系统的稳定性、可控性及加载频带的需求,设系统做正弦运动并基于以下约束条件确定的弹簧杆刚度系数范围。
设施加频率为f,幅值为T的正弦扭矩,则需实时加载的扭矩方程为:
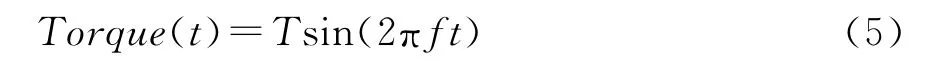
另设舵机端伺服不动,以及舵机本身刚度远大于弹簧杆刚度,并基于上述假设传动轴为刚性连接,加载电机运动方程为:

Am为加载电机运动幅值,则有:

由式(6)可得力矩电机角速度及角加速度:
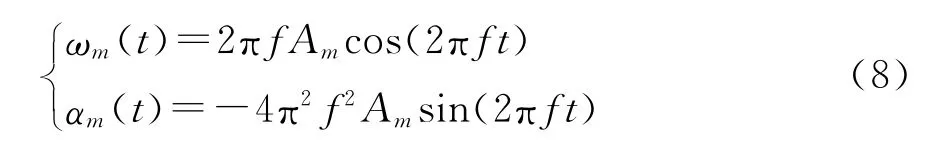
系统工作时,电机角速度及角加速度始终处在电机本身额定角速度及最大加速能力之内。根据电机转矩方程,假设电机工作在低频状态,此时,可忽略电机因阻尼引起的扭矩损耗,得到与舵机输出轴脱开时,电机最大角加的速度为:

Tmax为电机能够输出的最大力矩;Jm为系统总的转动惯量,由电机转动惯量和折算到电机轴上等效负载转动惯量组成。由式(7)~式(9)可得:

由式(10)可看出,弹簧杆刚度值存在最小下限;另外,为避免引起机械谐振,应提高系统固有频率,使其处在跟踪系统的通频带以外,即

综合式(10)和式(11),由表1中的参数,针对不同舵机承受力大小范围的不同,取弹簧杆刚度KL为2091N·m/rad和4184N·m/rad,在加载不同力矩时选择不同的弹簧杆以获取最佳加载性能。

表1 系统参数表
4 控制器设计

图2 控制系统
由上述系统数学模型得出的控制系统如图2所示。系统采用了多环级联嵌套的控制模式,即最外环为力矩闭环控制,而内环又是由加载电机位置、速度及电流三环组成的位置控制。
图2中,Gr(s)与θr(s)分别为舵机整体位置传递函数模型与位置指令;Gtra(s)及KF分别为力矩控制器及前馈系数。舵机的主动运动在弹簧杆末端会对加载系统形成位置扰动,该扰动不仅严重影响加载力矩精度,还会影响系统稳定性,即抑制多余力矩是该类被动加载系统面临的主要问题。系统根据不变性原理,在引入力矩前馈控制回路的基础上构成两自由度控制系统[6],即引入舵机角度补偿以抑制扰动力矩,其控制原理如图3所示[4]。

图3 不变性原理
由图3可知,为消除舵机角度变化产生的扰动,GF(s)应满足GN(s)=GF(s)G(s)。指令力矩到系统输出转矩的传递函数G(s)及舵机角至输出转矩的传递函数GN(s)为:

由此可见,若位置环Gp(s)基于比例控制、速度环Gv(s)基于比例积分控制,式(12)中4项分别对应补偿由舵机角加速度变化率、角加速度、角速度和角度产生的干扰力矩。前3项具有高阶微分,在工程中较难实现。实际应用时仅选取第4项,即在控制系统引入舵机角度补偿;同时,为提高内环位置控制精度,进而确保力矩外环力加载精度,还可基于位置环引入速度前馈与加速度前馈。
5 实验验证与分析
基于前述系统结构与控制结构,并根据实际需求,研制的反操纵测试设备最大加载能力为500N·m。在验证设备最大承载能力测试中,为避免直接加最大力矩时过冲对设备结构及传感器造成损害,在最外力矩闭环的基础上,位置内环采用S曲线加减速功能实现对力的平滑加载,从0N·m以10 N·m步长逐渐加载至500N·m,并同样以该步长递减回到0N·m。实验表明,无论正向与反向,都能实现最大500N·m扭矩加载指标,通过结构优化,并由大量调试经验,针对不同加载力而分段采用PID参数自适应控制,获得良好的力对称性及系统稳定性。
根据某型号舵机正反操纵力矩指标,对舵机进行实际测试,图4给出了对舵机施加100N·m反操纵负载力矩的实测曲线。左侧Y轴坐标代表加载电机与舵机的位置数据,右侧Y坐标代表加载扭矩大小。反操纵扭矩加载过程:舵机与加载电机归零后,同时偏离平衡位置做正向运动,而后在约0.7 s时,由于两者位置差的存在便向舵机施加100N·m的扭矩并维持,最终舵机会产生10°的舵偏角,在约1.7s时将力释放,舵机与加载电机同步回到初始点。
图5给出了对该舵机同时进行反操纵-正操纵扭矩加载实测曲线。反操纵阶段对舵机施加50N·m的扭矩,并拖动舵机产生10°舵偏角,而正操纵阶段维持给定扭矩并最终同时回到平衡位置。由前述定义,反操纵阶段模拟负载设备对舵机轴产生的扭矩方向与舵机运动方向一致,舵偏角不断加大;正操纵阶段模拟负载设备对舵机产生的扭矩方向与舵机运动方向相反,电机与舵机维持扭矩大小,实验最终回到平衡位置,舵偏角趋于零。图5中,位置差满足式(3)关系。
在正反操纵阶段,加载电机与舵机在维持扭矩大小运行过程中,一旦舵机位置受到扰动而使扭矩改变时,由高精度的编码器测出舵机角度变化,由系统内部位置、速度及电流环及时做出响应,保证舵机与电机保持良好同步运行状态;而力的变化大小由扭矩传感器测出并由力矩外环及时校正,可以有效地抑制多余力矩的产生,能够确保加载力矩的准确性。
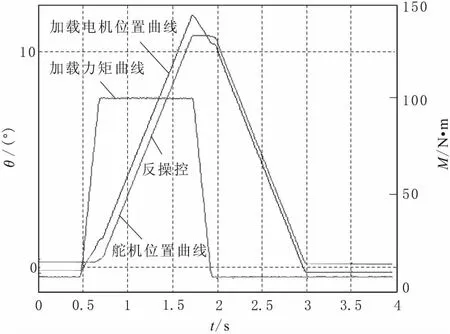
图4 反操纵实测曲线

图5 正反操纵实测曲线
6 结束语
随着科技的不断发展,基于电动的扭矩加载系统对舵机进行反操纵力矩加载已成为现实。为满足对新型舵机反操纵负载模拟测试的需求,研制了基于电动加载的大扭矩反操纵负载模拟设备。由于电动加载系统便于加载梯度、操纵力矩方向等参数的设置。因此,本设备不仅方便实现正反操纵力矩负载模拟,也可实现对舵机任意信号如正弦、方波力矩谱的加载测试。
系统获得了良好的正反操纵力矩模拟加载性能,而且结构紧凑,加载力精确度高,对称性和线性度好。同时,针对舵机不同的承载能力可设计不同刚度系数的弹簧杆,并选择合适控制参数以获得最佳力矩加载性能。实际测试表明,在一定舵偏角及加载力幅值下,在模拟正弦扭矩信号加载时能够满足工程上的双五、双十指标,加载频宽不小于20 Hz。该设备已交付用户使用,实现了预期的设计指标,并获得了满意的效果。
[1]曹 彤,孙杏初,欧阳沁,等.舵机反操纵负载台设计[J].北京航空航天大学学报,2003,29(3):252-254.
[2]王明彦.电动负载模拟技术的研究[D].哈尔滨:哈尔滨工业大学,2004.
[3]范金华.航弹舵机加载测试系统研究[D].长沙:国防科学技术大学,2007.
[4]Wang Xin,Feng Dongzhu.A study on dynamics of electric load simulator using spring beam and feedforward control technique[A].IEEE Chinese Control and Decision Conference[C].2009.301-306.
[5]符文星,朱苏朋,孙 力.弹簧杆刚度对电动负载模拟器的性能影响研究[J].弹箭与制导学报,2009,29(2):286-288.
[6]王维杰,李东海,高琪瑞,等.一种二自由度PID控制器参数整定方法[J].清华大学学报(自然科学版),2008,48(11):1962-1966.
