水平蒸汽发射系统的控制策略

严志腾，金家善，朱 泳

(海军工程大学动力工程学院，湖北 武汉 430033)

0 引言

水平蒸汽发射系统主要由蒸汽蓄热器、发射阀、汽缸、活塞组件、载荷等部件以及连接它们所布置的蒸汽管路组成，其工作原理为:通过发射阀的控制，蒸汽蓄热器内蒸汽在极短时间内流入汽缸并建立起汽缸内的压力，从而推动载荷向前运动，使载荷在达到规定的位移时达到规定的速度。

类似的系统还有气动式水下武器发射器［1］、舰载蒸汽弹射系统［2］和潜射导弹弹射系统［3］等，它们都是在极短时间内将高压工质的内能转化为用气(汽)负荷动能的弹射动力系统。目前，针对弹射动力系统的仿真建模及优化设计，已经做了大量的研究工作［4-6］，但国内对以水蒸气为高压工质的弹射动力系统的研究还较少，尤其是对系统性能进行优化设计的研究，目前还没有相关的成果报道。

由系统的工作原理可知，发射阀的开阀规律直接影响到系统的性能，故发射阀的开阀规律直接构成了系统的控制策略。本文通过对发射阀的开阀规律进行研究，以尽可能使系统的性能达到最优，从而得到系统的最优控制策略。

1 系统建模

系统中相关参数如下:P0和T0分别为蒸汽蓄热器内湿蒸汽压力 (MPa)和温度 (℃)，h0，ρ0和V0，a分别为蒸汽蓄热器内工质的比焓 (kJ/kg)、密度 (kg/m3)和体积 (m3)、充水系数，上标'和″分别代表湿蒸汽的水部和汽部参数;Q为瞬时放汽流量，kg/s;Pc为汽缸内压力，MPa;hc，ρ0和Vc分别为汽缸内工质的比焓、密度和体积;Dp为活塞直径，mm;mp，mf分别为活塞组件和载荷的质量，kg;Ap为蒸汽作用到活塞组件上的有效横截面积，m2;Ff为汽缸内壁的摩擦力，N;N为汽缸支持力。

1.1 蒸汽蓄热器热力学模型

依据变质量系统热力学理论［7］可知，蒸汽蓄热器内工质状态变化规律同时满足质量守恒方程、能量守恒方程和体积守恒方程。

蒸汽蓄热器内工质满足质量守恒方程:

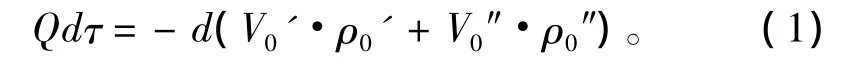
蒸汽蓄热器内工质满足能量守恒方程:

式中u0为工质比热力学能，kJ/kg。

该空间内工质同时满足体积守恒方程:

第二，在实行党政分开的过程中，由于行动过快，缺乏周密安排，形成了权力真空。在实行党政分开的政治体制方针后，戈尔巴乔夫提出一切权力归苏维埃，同时还大大精简政府行政机关和裁减人员。苏联政府原有51个部，后减为28个部。这样一来，政府的权力大大削弱了，政府十分软弱。最后使经济、经济改革等重大问题，处于“三不管”的局面：党无权管，最高苏维埃无力管，政府无法管。

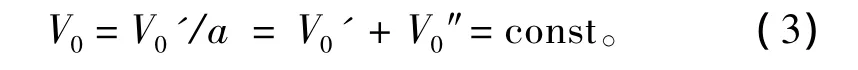
根据水和水蒸气热力性质可知，蒸汽蓄热器内湿蒸汽的汽部和水部状态函数都仅是压力或温度的单值函数，都可用水和水蒸气热力计算函数［8］得出:

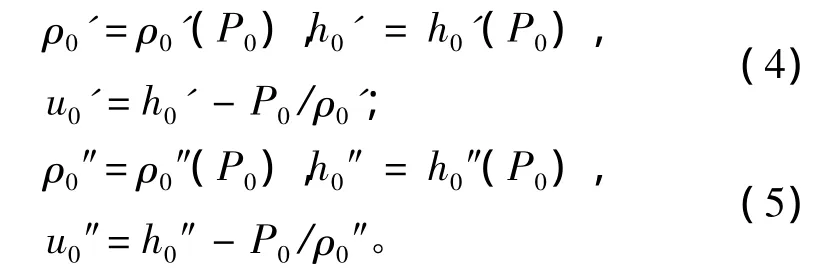
1.2 发射阀流量特性模型

流经发射阀的蒸汽流动分为阻塞流和非阻塞流2种情况，一般用临界压差比XT与比热比系数FK的乘积作为其产生阻塞流的临界条件。

当 X≥FK·XT时，为阻塞流［9］:

式中:X为压差比，X=(P0－Pc)/P0(Pc为汽缸内压力，MPa);FK=k/1.4(k为蒸汽的绝热指数，蒸汽过热时k=1.3;蒸汽饱和时k=1.135);XT的数值只决定于阀的流路情况及结构;y为膨胀系数，y=1－X/(3FK·XT);kv为流量系数，表征调节阀的流通能力，为发射阀相对开度l/L的函数。

当X ＜FK·XT时，为非阻塞流［9］:

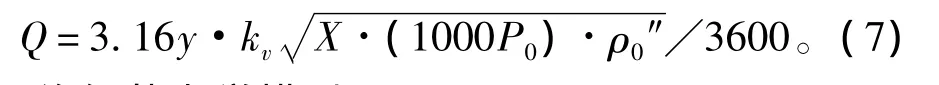
1.3 汽缸热力学模型

蒸汽流入汽缸的过程为变质量充汽过程，故汽缸内工质状态变化规律同时满足质量守恒方程和能量守恒方程。

汽缸内工质满足质量守恒方程:

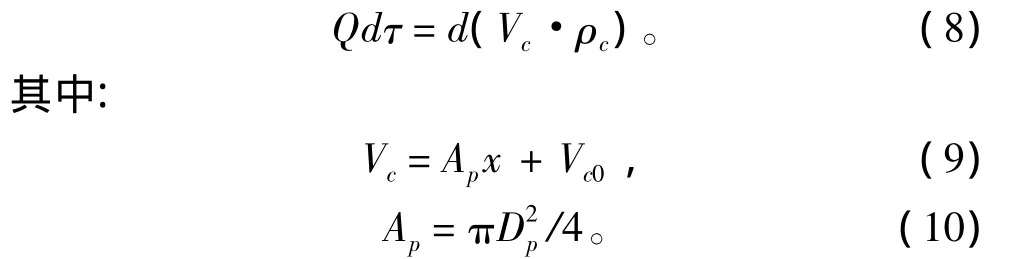
式中:Vc0为初始时刻汽缸的余隙容积;x为活塞组件及载荷的动力行程，m。

式中uc为汽缸内蒸汽比热力学能，kJ/kg。

汽缸内水蒸汽状态参数为压力和密度的函数，都可用水和水蒸气热力计算函数［8］得出:

1.4 活塞组件和载荷动力学模型

活塞组件和载荷沿加速度方向的运动方程为

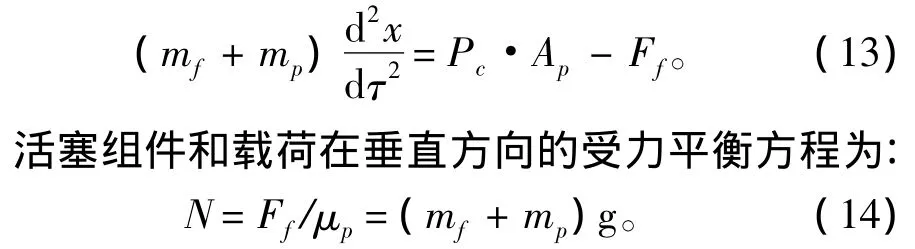
至此，由式(1)～式(14)联立所组成的方程组，即为水平蒸汽发射系统的动态数学模型。通过该模型对系统发射过程进行数值仿真，就可得到相应的系统性能参数随时间变化规律，进而对系统的控制策略开展研究，以得到系统最优发射性能。

2 系统控制策略研究

2.1 系统仿真计算

基于已建立好的系统动态数学模型，在给定发射阀开阀规律为最简单的线性开阀，运用Matlab的Simulink平台，对系统的发射过程进行仿真，通过选择合适的发射阀Kv值，就可以使载荷在规定的动力行程 (无量纲值为0.82)达到规定的速度 (无量纲值为0.9)，或载荷速度超过规定值的额度最小。此时，载荷加速度随时间变化曲线如图1所示。图中数据均进行了归一化处理。

由图1可知，对数、直线和快开调节阀下载荷加速度的波动幅度依次增大，经计算，载荷加速度峰均比(加速度最大值与平均值之比)分别为1.27，1.46和1.60。显然，3种调节阀下载荷的加速度波动幅度都比较大，系统在这方面的发射性能并未达到最优。因此，有必要开展系统控制策略的优化研究，尽可能减小载荷的加速度波动幅度，全面提高系统的发射性能。

图1 载荷无量纲加速度随无量纲时间变化曲线Fig.1 Dimensionless load acceleration profiles as a function of dimensionless time

2.2 系统控制策略的优化和结果分析

由图1可以看出:在放汽初始阶段，3种阀下载荷加速度迅速达到峰值，且直线和快开调节阀下载荷加速度峰值较大，而对数调节阀下载荷峰值较小;随着放汽过程的不断进行，直线和快开调节阀下载荷加速度迅速下降，而对数调节阀下载荷加速度则经历了一个先下降后上升的过程。其原因主要是由调节阀的理想流量特性造成的:在发射初期 (t*小于0.1左右)，对于直线和快开调节阀，在线性开阀的系统控制策略下，流量系数增速过快，使得进入汽缸内蒸汽流量迅速增加，汽缸内压力也迅速提高，最终造成载荷加速度峰值过高;而对于对数调节阀，在线性开阀下，流量系数增速相对较慢，从而造成载荷加速度峰值较低。随着发射过程的不断进行，直线和快开调节阀的流量系数增速小于对数调节阀的流量系数增速，故快开调节阀和直线调节阀下，载荷加速度下降速度大于对数调节阀下载荷加速度下降速度;在发射后期，对数调节阀下流量系数远大于直线和快开调节阀流量系数，使得进入汽缸内蒸汽建立起的压力的影响大于活塞组件做功时容积扩大而减小压力的影响，故载荷加速度逐渐上升，而直线和快开调节阀下流量系数相对过小，使得进入汽缸内蒸汽建立起的压力的影响小于活塞组件做功时容积扩大而减小压力的影响，故载荷加速度仍逐渐下降。

由上分析可知，要使载荷加速度峰均比接近1，就需使载荷加速度峰值不能过高，且载荷加速度达到峰值后尽可能保持水平，而不是迅速下降 (如直线和快开调节阀)或先下降后上升 (对数调节阀)。故在发射初期，对于直线和快开调节阀，需降低阀的开阀速度，以降低发射阀流量系数，进而减小进入汽缸内蒸汽流量来降低汽缸内压力，从而降低载荷加速度的峰值;而对于对数调节阀，需提高阀的开阀速度，以提高发射阀的流量系数，进而增加进入汽缸内蒸汽流量来提高汽缸内压力，从而提高载荷加速度的峰值。随着发射过程的进行，对于直线、快开和对数调节阀，都需提高阀的开阀速度，以提高发射阀的流量系数，进而增加进入汽缸内蒸汽流量来提高汽缸内压力，从而维持载荷尽可能的做匀加速运动;而在放射后期，对于对数调节阀，需降低阀的开阀速度以降低发射阀流量系数，以减少进入汽缸内蒸汽流量来降低汽缸内压力，从而降低载荷加速度来维持载荷做匀加速运动。

依据以上关于系统控制策略的分析，基于Matlab的Simulink仿真平台，通过调整发射阀的开阀规律，对系统进行优化设计，可以得到在发射过程尽可能平稳的前提下3种不同类型发射阀的开发规律，如图2所示。这里注意到，由于3种调节阀下载荷动力行程相同，且载荷加速度到达峰值后波动幅度非常小，故3种调节阀下系统相关参数随时间变化曲线基本一致。

图2 阀相对开度随无量纲时间变化曲线Fig.2 Relative opening profiles of launching valve as a function of dimensionless time

由图2可知，在相同的无量纲时间下，对数调节阀相对开度最大，直线调节阀次之，快开调节阀下最小。其中，在对数调节阀下，在放汽初始阶段，当无量纲时间仅为0.05时，发射阀相对开度迅速从0增加至0.2;随着发射过程的不断进行，发射阀开阀速度逐渐减缓，直至开度达到最大值1，放汽过程结束。在直线和快开调节阀下，在放汽初始阶段，发射阀开阀速度很慢，当无量纲时间分别为0.29和0.51时，直线和快开调节阀的相对开度才从0增加至0.2，随后2种阀的开阀速度逐渐增加，且快开调节阀开阀速度较直线调节阀增加的快。总的来说，直线调节阀动作过程最为平稳，快开调节阀次之，对数调节阀最剧烈。

图3为载荷无量纲加速度、速度及位移随无量纲时间变化曲线。由图可知，载荷峰均比为1.03，载荷近似做匀加速运动，系统运行安全性得到很大提高。载荷无量纲速度随无量纲时间变化曲线近似为二次曲线，而载荷位移随时间近似于线性增加。

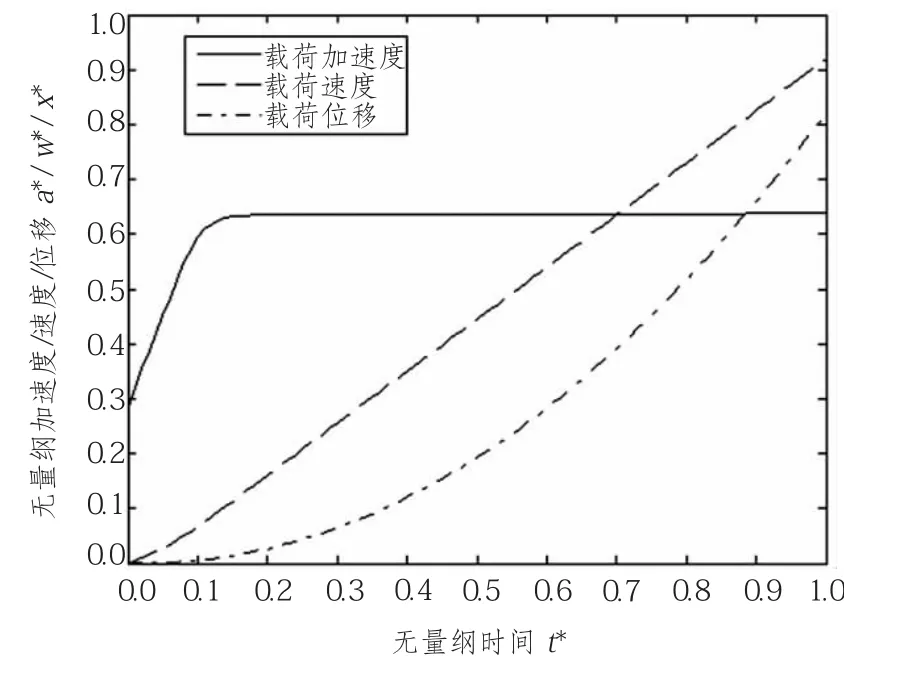
图3 载荷无量纲加速度、速度及位移随无量纲时间变化曲线Fig.3 Dimensionless acceleration，velocity and displacement profiles of load as a function of dimensionless time

综上所述，在3种不同类型发射阀中，选取直线调节阀，能使载荷峰均比近似为1时，载荷在达到规定的位移时对应的速度超过规定值最小，且发射阀动作过程最为平稳。

3 结语

通过建立水平蒸汽发射系统的动态数学模型，基于Matlab的Simulink平台对水平蒸汽发射系统进行优化设计。结果表明，在3种不同类型的发射阀中，在保证载荷达到规定的位移时载荷速度超过规定值最小且载荷基本上做匀加速运动的情况下，直线调节阀下阀的动作过程最为平稳。

［1］练永庆，王树宗，陈一雕.气动式水下武器发射器内弹道优化研究［J］.弹道学报，2002，14(2):1-5，12.LIAN Yong-qing，WANG Shu-zong，CHEN Yi-diao.Optimal study on the underwater weapon's interior trajectory of compressed-air launcher［J］.Journal of Ballistics，2002，14(2):1-5，12.

［2］程刚，倪何，孙丰瑞.舰载蒸汽弹射系统建模与仿真研究［J］.武汉理工大学学报(交通科学与工程版)，2010，34(2):301-305.CHENG Gang，NIHe，SUN Feng-rui.Modelingand simulation research on naval steam-power aircraft launch system［J］.Journal of Wuhan University of Technology(Transportation Science ＆ Engineering)，2010，34(2):301-305.

［3］CHEN Qing-gui，ZHOU Yuan，WANG Hai-yang，et al.Submarine-launched cruise missile ejecting launch simulation and research［C］.Proceedings of the 2011 IEEE International Conference on Electronic and Mechanical and Information Technology，Harbin:IEEE，2011:4542-4545.

［4］廖振强，王涛，何大平，等.抛放弹弹射机构优化设计［J］.南京理工大学学报，2002，19(3):259-263.LIAO Zhen-qiang，WANG Tao，HE Da-ping，etal.Optimization of blank cartridge ejection device［J］.Journal of Nanjing University of Science and Technology，2003，27(5):573-577.

［5］陈庆贵，齐强，周源，等.发射动力系统内弹道优化设计计算［J］.舰船科学技术，2011，33(5):91-97.CHEN Qing-gui，QI Qiang，ZHOU Yuan，et al.Interior trajectory optimization design and computation of launching power system［J］.Ship Science and Technology，2011，33(5):91-97.

［6］HAO Xin，WANG Jian-zhong，SHI Jia-dong，et al.Modeling and simulation on the interior ballistics of piston high-lower pressure launch device for micro-robot［C］.Proceedings of the 2012 IEEE International Conference on Modeling，Identification ＆ Control，Wuhan:IEEE，2012:366-370.

［7］吴沛宜，马元.变质量系统热力学及其应用［M］.北京:高等教育出版社，2001.WU Pei-yi，MA Yuan.The application of variable mass system thermodynamics［M］.Beijing:Higher Education Press，2001.

［8］WAGNER W，COOPER J R，DITTMANN A，et al.The IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam［J］.Journal of Engineering for Gas Turbines and Power，2000，122(1):150-182.

［9］吴国熙.调节阀使用与维修［M］.北京:化学工业出版社，1999.WU Guo-xi.Operation and maintenance of control valve［M］.Beijing:Chemical Industry Press，1999.