气象误差辨识提高舰炮一维修正弹预测落点精度
2013-08-26汪汇川解维河苏轼鹏孙续文
黄 义,汪汇川,解维河,苏轼鹏,孙续文
(海军大连舰艇学院,辽宁 大连 116018)
0 引言
一维弹道修正弹是一种低成本信息化弹药,与普通弹药相比,射弹密集度大幅提高[1],解决了舰炮发射无控弹射击精度低的难题。在一维弹道修正中,如何由实测的一段弹道参数,实时、准确地解算出落点射程,是极其重要的环节之一[2],也是弹道修正弹武器系统研制亟待解决的关键技术之一。目前,利用弹丸最小速度值及其出现时间进行弹道辨识,以及基于速度时间序列进行弹道辨识的方法均有各自的缺陷[3]。基于比较名义弹道与实际弹道上升初始段弧长实现对射程偏差预测的方法[4],要求测量名义弹道前1/4弧长对应时间段内的实际弹道,这样雷达测量弹道需要占用较多的时间,限制了火炮的发射速度,制约了火炮作战效能的充分发挥。实践表明,气象误差是现代火炮射击的主要误差,为了由实测的一段弹道坐标实时、准确地预测落点射程,本文提出对实测弹道坐标滤波、利用弹道坐标滤波值和预定弹道坐标的偏差辨识气象误差、通过解弹道方程预测落点的一种方法,并进行精度分析。
1 一维修正弹弹道模型
对已获取较准确的气动力参数且飞行稳定性良好的炮弹,用实测的弹道参数作为初始条件进行质点弹道计算,同实际弹道非常接近,有良好的计算精度,所以,弹道修正控制解算多采用质点弹道模型[2]。一维弹道修正弹仅对射程进行修正,选择弹道方程为

根据式(1),如果弹道系数、初速、射角和气象条件已知,则落点可确定。实际上弹道系数、初速、射角和气象条件不可能与发射前计算射击诸元所用的数值完全一致,这将导致雷达实际测量的一段弹道坐标与理论计算的弹道坐标不一致。雷达可以测量弹道坐标和速度,并且通过滤波可以消除测量噪声的影响,但是由于气象误差是射击误差的主要因素之一,所以,充分利用弹道参数预测值和测量值之间的偏差识别气象误差是精确预测落点的关键。
2 气象误差分析
炮兵规定地面标准温度15℃,相对湿度50%,地面标准虚温τ0N=288.9°K,虚温随高度分布的标准定律如图1所示。当只能获得地面实际虚温与标准虚温偏差时,则各高度的虚温按照虚温随高度的标准定律加上地面虚温偏差的方法确定,称为标准分布。由于实际气象条件是复杂的,实际分布与标准分布之间存在误差。即使有气象保障的条件下,仍有测量误差、射击时间与测量时间不一致误差和射击区域与气象站空间不一致的误差。
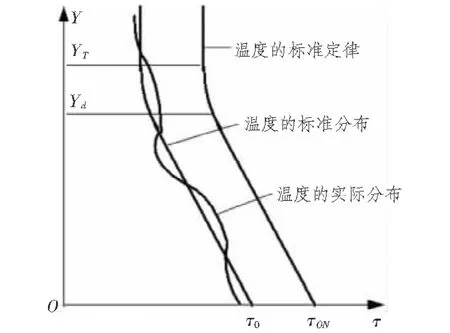
图1 虚温随高度分布图Fig.1 Virtual temperature distributing chart going with height
在大气处于铅直平衡状态的假设下,大气压力随高度的关系式为

式中:p0为地面气压;R1=29.27。
目前,气象通报中只发布地面气压值而不包括各高度上的实际气压,但是,大气复杂的动态运动使按式(2)计算的气压与实际气压存在误差[5]。虚温和气压误差直接使式(1)中空气密度和声速产生误差,进而使预测落点射程产生误差。另外,实际风和测量风的误差[6]也会对预测落点产生误差。
3 气象误差辨识方法
文献 [7-9]研究了对虚温和纵横风的辨识方法、按照式(2)计算气压,而计算所得气压与实际气压之间的误差必将使预测落点产生误差;另一方面,文献 [7-9]的辨识方法适合炮兵采用试射、效力射2个阶段传统的射击方法,而弹道修正弹要求在每发炮弹落地前预测落点,并且要给修正指令的形成、发送和修正执行机构工作留下足够的时间。本文借鉴舰炮射击将弹道气象误差折算成初速误差的传统做法,提出一种将全部气象误差折合成某一种气象误差用于一维弹道修正弹落点预测的方法。
借鉴弹道风的定义[10],假设全弹道只有气压有一常值误差,称之为等效气压误差,此误差对射程的影响与实际气温、湿度、气压、风速、风向等全部误差对射程的影响相等。等效气压误差的求法为:设雷达实际测量一段弹道坐标转换到射击坐标系X轴 (射击方向)上的坐标为(i=1,2,…,n),滤波值为(i=1,2,…,n),二者之差绝对值最小值(k∈i,i=1,2,…,n),k为二者之差绝对值最小时的i;设(i=1,2,…,n)的对应时刻射击坐标系X轴上的事先预测坐标为(i=1,2,…,n);设全弹道只有气压有一常值误差Δp,解弹道方程得(i=1,2,…,n)的对应时刻射击坐标系X轴上的坐标为(i=1,2,…,n),则等效气压误差Δpe按下式计算:
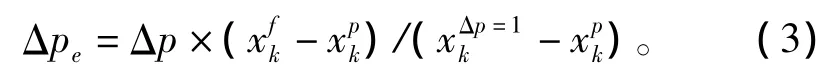
用求得的Δpe和实际测量弹道坐标、速度转换到射击坐标系后坐标、速度的滤波值,通过解弹道方程推算落点。以上为等效气压误差法识别气象误差用于一维弹道修正弹落点预测。同理,还有等效虚温误差法和等效纵风误差法。
4 仿真
以某型弹为例,射角35°,雷达测量弹丸飞行时间16~22 s的弹道坐标,仿真气象误差分为无风误差、顺风误差和逆风误差3种情况,每种情况下虚温、气压误差分为8种情况,风误差均值为2.0 m/s,均方差0.2 m/s。虚温、气压误差如表1所示,虚温误差单位为°K,气压误差单位为地面标准气压 (p0N=1000 hPa)的百分比,虚温误差均方差为0.1°K,气压误差均方差为0.1%p0N。分别采用等效虚温误差、等效气压误差和等效纵风误差3种方法辨识气象误差,与不辨识气象误差预测落点的射程误差如表1所示。

表1 射程误差Tab.1 Range errors
从表1可以看出:
1)等效虚温误差法和等效气压误差法预测落点精度,从均值和均方差二方面综合比较明显好于不识别气象误差预测落点的精度;
2)等效纵风误差法分别在无风误差、顺风误差、逆风误差3种情况下,预测落点误差均值明显好于不识别气象误差;
3)从推算落点误差的均值和均方差两方面综合考虑,等效气压误差法好于等效虚温误差法和等效纵风误差法以及不识别气象误差,射程误差均值为-7.58 m、均方差为10.97 m,满足一维弹道修正弹落点预测的精度要求。
5 结语
本文提出的方法利用实测弹道坐标滤波值与预测弹道坐标的偏差、将全部气象误差折算成某一种气象误差、通过解弹道方程预测一维弹道修正弹落点,克服了现有弹道辨识算法的局限性,适应一维弹道修正弹火控解算的需要。除了表1所列数据外,笔者做了多种情形下的仿真,均表明本文的方法能够满足一维弹道修正弹预测落点的精度要求。研究结论为一维弹道修正弹预测落点技术提供参考。
[1]史金光,王中原,等.一维弹道修正弹气动力计算方法和射程修正量分析[J].火力与指挥控制,2010,35(7):80-83.SHI Jin-guang,WANG Zhong-yuan,et al.Aerodynamic calculational method and range correction analysis of one dimensional trajectory correction projectile[J].Fire Control and Command Control,2010,35(7):80 -83.
[2]王中原,史金光,李铁鹏.弹道修正中的控制算法[J].弹道学报,2011,23(2):19 -21,27.WANG Zhong-yuan,SHI Jin-guang,LI Tie-peng.Control method for trajectory correction[J].Journal of Ballistics,2011,23(2):19 -21,27.
[3]李岩,任睿,王旭刚.两种卡尔曼滤波模型在修正弹弹道数据处理中的应用研究[J].弹道学报,2011,23(1):27-30.LIYan, REN Rui, WANG Xu-gang. Application comparision oftwo Kalman filtering modelsused in trajectory data processing of correction projectile[J].Journal of Ballistics,2011,23(1):27 -30.
[4]侯宏录,闫帅.利用Simulink仿真的弹道辨识算法精度分析[J].西安工业大学学报,2008,28(5):409 -413.HOU Hong-lu,YAN Shuai.Accuracy analysis of trajectory identification algorithm based on Simulink simulation[J].Journal of Xi'an Technological University,2008,28(5):409-413.
[5]王兆胜,郭锡福.气压偏差对射击诸元精度的影响[J].弹箭与制导学报,2001,21(4):70 -72.WANG Zhao-sheng,GUO Xi-fu.The influence on accuracy of firing element by deviation of air pressure[J].Journal of Projectiles,Rockets,Missiles and Guidance,2001,21(4):70-72.
[6]王建明,潘红华,许涛.舰载火箭炮弹道风确定探讨[J].弹道学报,2004,16(1):11 -15.WANG Jian-ming,PAN Hong-hua,XU Tao.Study of naval ramming system ballistic-wind correct coefficient[J].Journal of Ballistics,2004,16(1):11 -15.
[7]汪德虎,戴耀,王建明.舰炮弹道观测校正研究[J].弹道学报,2002,14(2):48 -51,56.WANG De-hu,DAI Yao,WANG Jian-ming.Study of naval gun's trajectory detection and correction[J].Journal of Ballistics,2002,14(2):48 -51,56.
[8]戴耀,汪德虎,马野.基于神经网络逆模型的非线性外弹道参数辨识[J].弹道学报,2005,17(1):18-22.DAI Yao,WANG De-hu,MA Ye.Study of nonlinear ballistic parameters identification based on neural network contrary model[J].Journal of Ballistics,2005,17(1):18-22.
[9]赵金强,汪德虎.舰炮间瞄射击的辨识修正方法[J].弹道学报,2006,18(2):91 -93,96.ZHAO Jin-qiang,WANG De-hu.Identification correction method of indirect aiming firing of shipboard guns[J].Journal of Ballistics,2006,18(2):91 -93,96.
[10]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.HAN Zi-peng.Exterior ballistics of projectiles and rockets[M].Beijing:Beijing Institute of Technology Press,2008.
