三体船波浪载荷预报研究
2013-08-26耿彦超胡嘉骏顾学康汪雪良
耿彦超,胡嘉骏,顾学康,汪雪良,张 凡
(中国船舶科学研究中心,江苏 无锡 214082)
0 引言
三体船作为一种新型高性能船,已经引起造船界学者的兴趣,一些造船技术先进的国家已经在这方面开展了一系列的研究工作,并建造了实船。
根据现有高速三体船的相关资料和海浪统计资料,本文采用三维频域计算方法,给出横纵向波浪载荷分量的传递函数 (RAO)及长短期预报值。横向波浪载荷包括各纵剖面的横向对开力、横垂向剪力、横垂向弯矩、纵摇有关扭矩等;纵向波浪载荷包括各横剖面的纵垂向剪力、纵垂向弯矩、纵向扭矩和水平弯矩[1]。
根据本文的计算结果,可给出高速三体船的波浪载荷特征,为结构的进一步优化设计提供重要依据,并为相关规范公式的修改提供参考。
1 波浪载荷预报
设三体船在水面上做任意形式的摇荡运动,运动由入射波及其在船体上的绕射影响所引起。流体或船体的初始位置和速度已知。图1描述波浪和三体船舶运动及3个右手坐标系[2-3]。

图1 三体船运动坐标系Fig.1 The reference frame of trimaran motions
1)空间固定坐标系O-XYZ:原点O位于未扰动的静水面上,OX轴与入射波浪传播方向相反,OZ轴竖直向上,用这个空间固定坐标系来表示入射波最为方便。
2)随船平动坐标系o-xyz:原点o位于未扰动的静水面上,ox轴与船舶航行方向一致,oz轴竖直向上,通过船舶重心,oxy平面与静水面重合。
3)固连船体坐标系G-xbybzb:原点G为船舶重心,Gxb轴平行于船体基线指向船首,Gzb轴垂直于船体水线面,用这一坐标系表述船体表面。
通过势流理论确定场内速度势后,按线性伯努利方程求得流场中的动压力和作用于船体上的流体动力,并以此建立起时域运动方程,得到船体的运动。当入射波是规则的简谐振荡波,船体的运动也简谐。时域运动方程可以转换成频域运动方程。对时域计算结果进行傅立叶变换后,得到频域下运动和剖面载荷的传递函数[4]。
波浪载荷预报的目的,是以规则波中的载荷响应为基础,通过理论计算,确定船舶在给定的时间运行于实际海情中的波浪载荷变化特性。波浪载荷预报常分为短期预报和长期预报2类。短期预报的时间范围为0.5 h到数小时,在此时间内,船的装载状态、航速、航向角以及海情都可以被认为固定不变。长期预报的时间范围是数年或整个寿命期,在此时间内,上述因素都会改变,长期预报由许多短期预报组成。一旦船舶运行海域和概率水平确定后,即可得到对应的波浪载荷特征最大值Xmax。此值表示船舶在波浪遭遇次数为n的整个使用期内,最可能出现的最大波浪载荷[5]。
2 模型建立与计算设置
计算对象为某高速三体船,该三体船主船体垂线长70 m,片体船体垂线间长28 m,三体船左右2个片体与主船体尾部对齐,主船体的排水量约为单独1个片体排水量的40倍。
建立高速三体船模型,然后生成船体表面和自由面网格。为计算精确,将船体分成主体部分、片体部分与连接桥3个部分,然后单独划分网格。自由面网格等见图2与图3。整理主船体,片体及连接桥结构重量分布,在考虑横摇惯性半径情况下建立质量模型。

图2 水动力计算模型Fig.2 The hydrodynamic model

图3 船体与自由面网格Fig.3 The gridding of hull and free surface
另外,在保证纵向惯量和横摇周期的情况下,建立除去2个片体只保留主船体的单体船水动力计算模型,如图4所示。模型吃水、船体表面和自由面网格尺寸、附体、阻尼等设置与三体船一样[6]。
计算假设船舶航行在无限水深海域,航向角从0°~180°(规定顶浪航行为 180°),共取13个航向,航向角定义如图5所示。计算波浪周期共取31个。采用IACS Rec.34北大西洋标准海浪统计资料,计算航速V分别取为0,10,18与24 kn。取0~20站共21个计算横剖面,沿船宽0到10站共11个计算纵剖面。
短期预报采用P-M双参谱;长期预报采用IACS推荐的Rec.34标准海浪统计资料 (2001年修正版)[7]。考虑到高速三体船适用于7级海浪要求,根据实际情况把海浪资料波高截断,即有义波高变化范围为0.5~6 m及0.5~9 m,其中6 m及9 m有义波高的出现概率按照插值的方法得到。在响应的长期预报时,对应的超越概率 Q分别为 10-2,10-4,10-6,10-8,10-10。为控制计算的发散,采用模拟数字舵技术控制船舶的横摇和首摇横向运动,采用模拟弹性系统控制纵荡运动。线性横摇阻尼取为0.05。

图4 单体船水动力计算模型Fig.4 The hydrodynamic model of hull
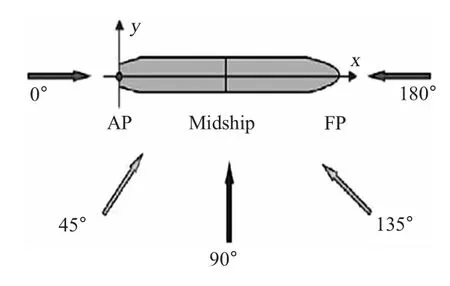
图5 航向角定义Fig.5 The describing of course angle
计算结果包括传递函数、短期预报和长期预报(见图6~图33)。图中LFy为横向对开力,LFz为横垂向剪力,LMx为横垂向弯矩,LMy为纵摇有关扭矩,VWSF为垂向波浪剪力,TM为波浪扭矩,VWBM为垂向波浪弯矩,HWBM为水平波浪弯矩。
3 传递函数的对比分析
V分别取为0,10,18与24 kn,给出高速三体船横纵向波浪载荷的传递函数,如图6~图13所示。横坐标为波长船长比,纵坐标为单位波幅下的响应幅值。
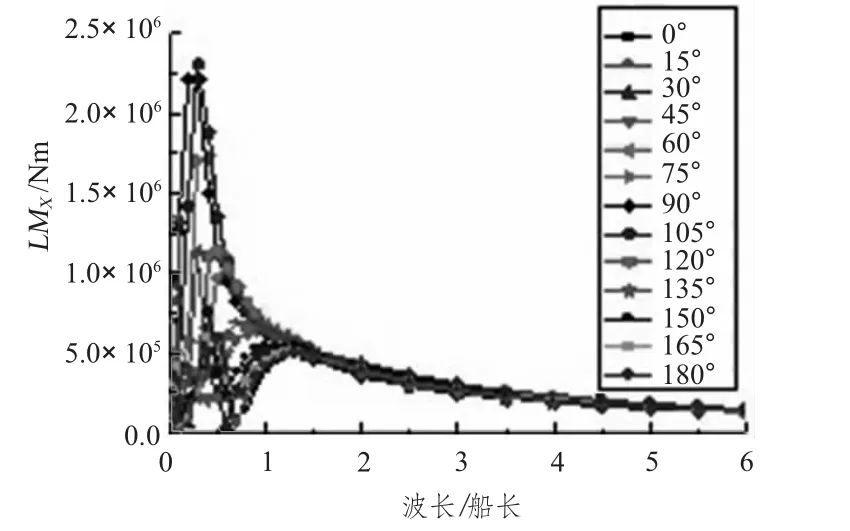
图6 0 kn横垂向弯矩传递函数Fig.6 The RAO of transverse prying moment(0 kn)

图7 0 kn纵摇有关扭矩传递函数Fig.7 The RAO of pitch connecting moment(0 kn)

图8 0 kn中纵向波浪扭矩传递函数Fig.8 The RAO of longitudinal torsion(0 kn)

图9 0 kn中纵垂向波浪弯矩传递函数Fig.9 The RAO of longitudinal prying moment(0 kn)

图10 180°中纵垂向波浪弯矩传递函数Fig.10 The RAO of longitudinal prying moment(180°)
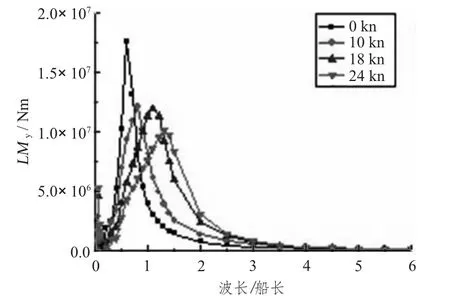
图11 135°纵摇有关扭矩传递函数Fig.11 The RAO of pitch connecting moment(135°)
3.1 相同航速传递函数对比分析
从同航速下传递函数可以看出:横向对开力在横浪时最大,随浪与顶浪时最小;同样横垂向弯矩也是在横浪时最大,随浪与顶浪时最小;而纵摇有关扭矩则是在首斜浪时最大。
首尾L/4剖面处的纵垂向剪力在顶浪时最大;纵向扭矩在首斜浪时最大;纵垂向弯矩在顶浪时最大;水平弯矩在首斜浪时最大。
3.2 相同浪向传递函数对比分析
从同浪向下的传递函数可以看出:顶浪时纵垂向弯矩的幅值随着航速的增大而增大;首斜浪时纵摇有关扭矩和纵向扭矩幅值随着航速的增大而减小且往低频方向移动;横浪时横垂向弯矩受航速变化影响不大。
4 波浪载荷的短期预报
三体船短期预报结果如图14~图17所示。横坐标为波浪平均跨零周期,纵坐标为单位有义波高下不同航速的响应值。同样,横向对开力和横垂向弯矩受航速变化影响不大;纵摇有关扭矩和纵向扭矩幅值随着航速的增大而减小且往低频方向移动;顶浪时纵垂向弯矩的幅值随着航速的增大而增大。
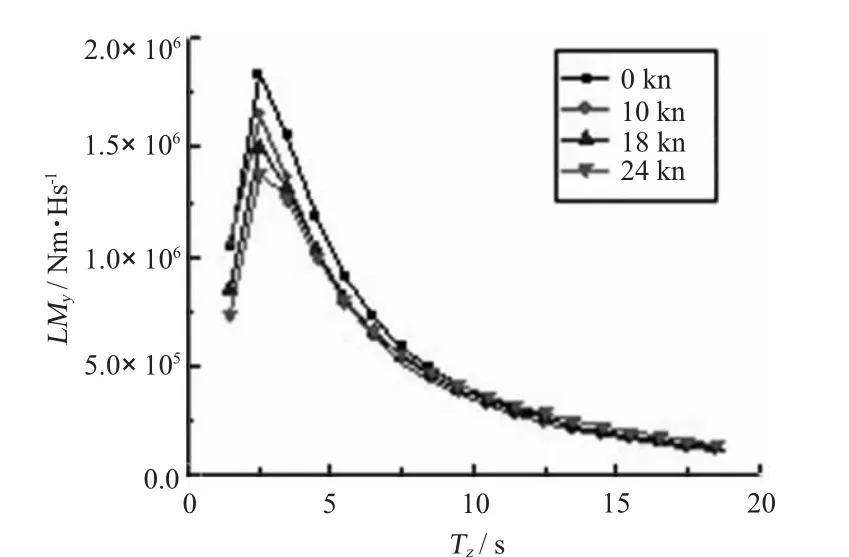
图15 135°纵摇有关扭矩短期预报Fig.15 The short term of pitch connecting moment(135°)
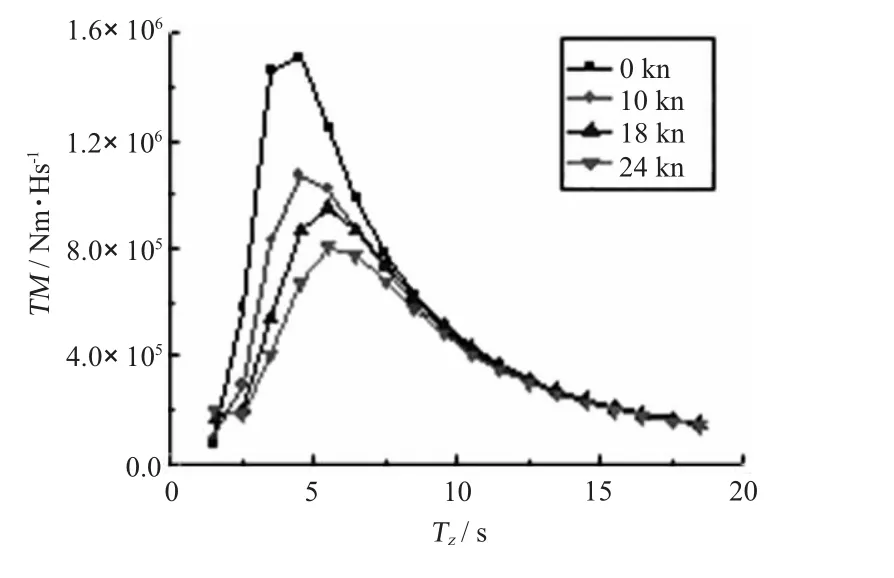
图16 135°舯纵向扭矩短期预报Fig.16 The short term of longitudinal torsion(135°)
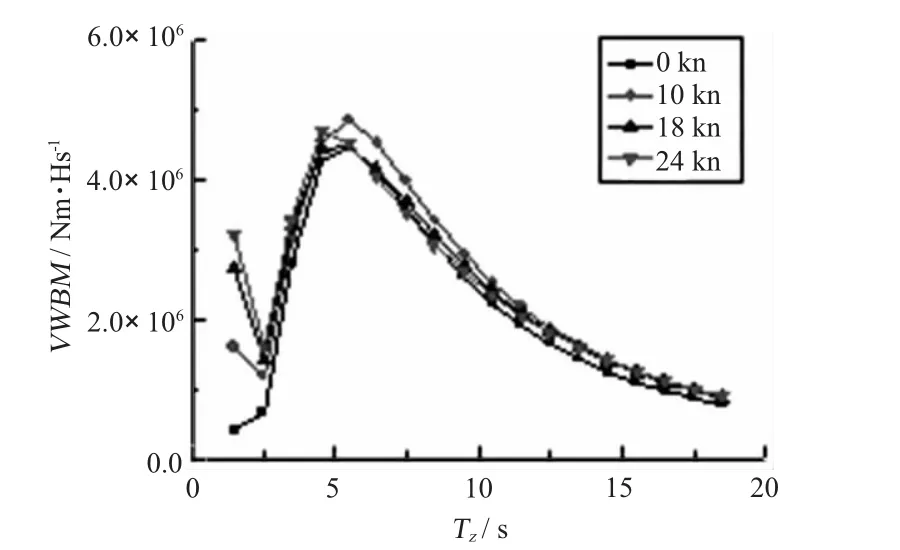
图17 180°舯纵垂向弯矩短期预报Fig.17 The short term of longitudinal prying moment(180°)
5 波浪载荷的长期预报
三体船波浪载荷长期预报结果如图18~图33所示。长期预报分别采用IACS 6 m极限有义波高和9 m极限有义波高等2种情况。长期预报根据V=0时的传递函数做出。
5.1 极限有义波高为6 m时横向波浪载荷沿船宽变化
三体船横向波浪载荷长期预报值沿船宽的变化如图18~图21所示。横坐标为沿船宽的站号,纵坐标为载荷的长期预报值,响应是单幅值。可以看出,横向对开力在中纵剖面处最大;横垂向剪力与横垂向弯矩随船宽变化曲线基本相同,都是在中纵剖面处最大,但是在连接桥与主体和片体连接区域也有个小峰值,且连接部分存在几何和结构的突变,容易引起应力集中,应引起设计者的高度重视;纵摇有关扭矩沿船宽方向也是在中部达到最大值。
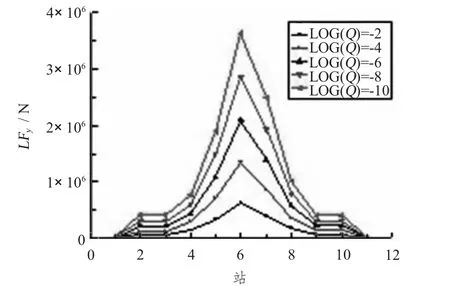
图18 横向对开力长期预报Fig.18 The long term of lateral shear force
5.2 极限有义波高为6 m时纵向波浪载荷沿船长变化
三体船纵向波浪载荷长期预报值沿船长的变化见图22~图25。横坐标为沿船长的站号,纵坐标为载荷的长期预报值,响应是单幅值。纵垂向剪力沿船长变化呈双峰现象,且靠近船尾处的峰值大于靠近船首处的峰值;纵向扭矩、纵垂向弯矩、水平弯矩都在船中附近取得最大值,且越靠近船首尾方向越小。
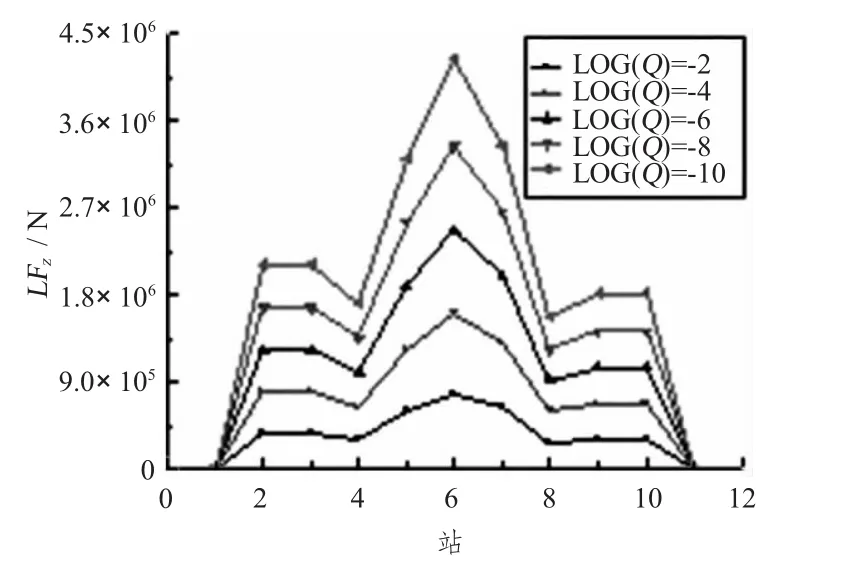
图19 横垂向剪力长期预报Fig.19 The long term of transverse vertical shear force
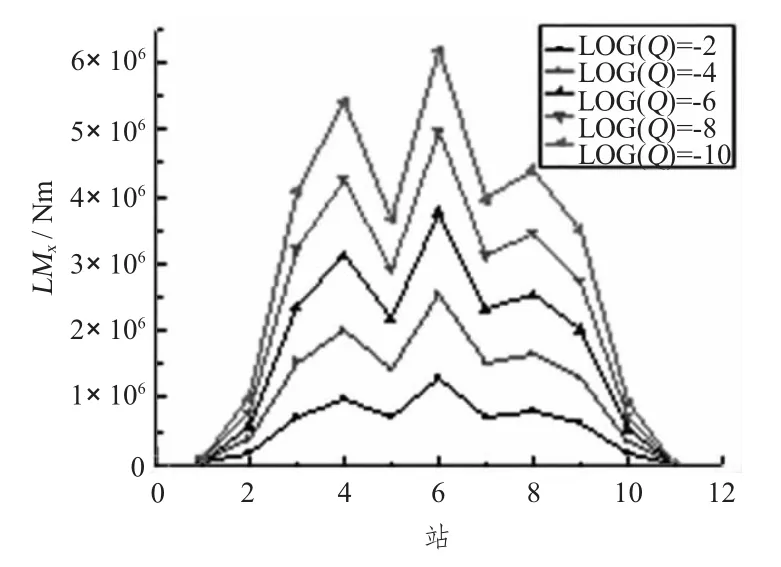
图20 横垂向弯矩长期预报Fig.20 The long term of transverse prying moment

图21 纵摇有关扭矩长期预报Fig.21 The long term of pitch connecting moment

图22 纵垂向剪力长期预报Fig.22 The long term of longitudinal vertical shear force

图23 纵向扭矩长期预报Fig.23 The long term of longitudinal torsion
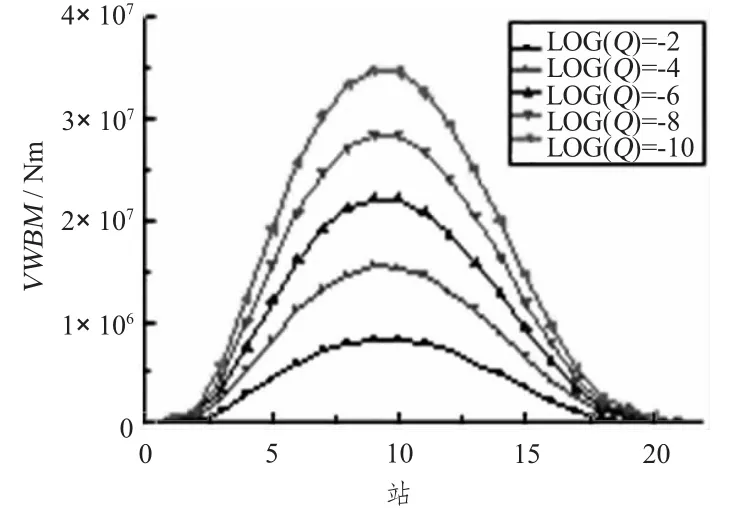
图24 纵垂向弯矩长期预报Fig.24 The long term of longitudinal prying moment

图25 水平弯矩长期预报Fig.25 The long term of horizontal moment
5.3 纵向波浪载荷受2个片体影响变化的对比分析
三体船纵向波浪载荷受2个片体影响长期预报值沿船长的变化见图26~图29。横坐标为沿船长的站号,纵坐标为载荷在极限有义波高为6 m时的长期预报值,响应是单幅值。其中Trimaran为三体船,Mainhull为除去2个片体只保留主船体的单体船。从图中可以看出,三体船长期预报结果与只有三体船主船体的长期预报结果基本相同,其中,三体船的纵垂向剪力、纵垂向弯矩与水平弯矩略大于单体船结果且趋势基本相同。而三体船纵向扭矩明显大于单体船纵向扭矩,表明三体船纵向扭矩与纵摇有关扭矩一样重要,需特别关注。
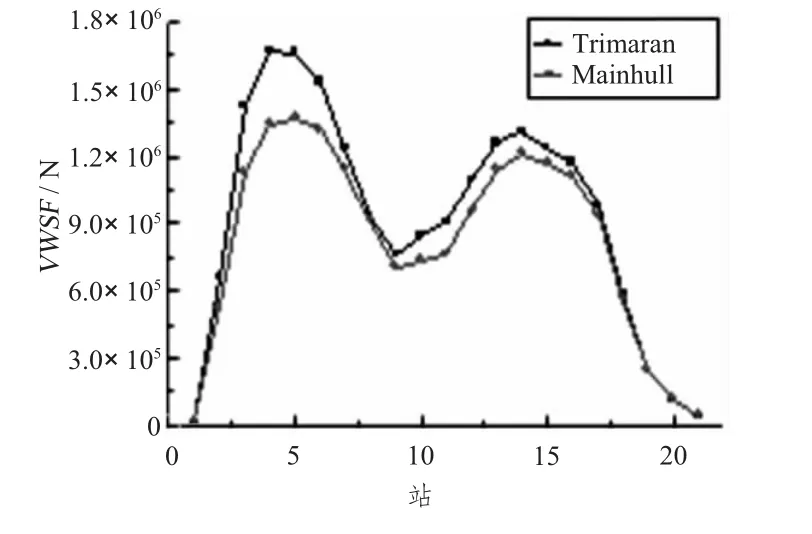
图26 纵垂向剪力长期预报Fig.26 The long term of longitudinal vertical shear force
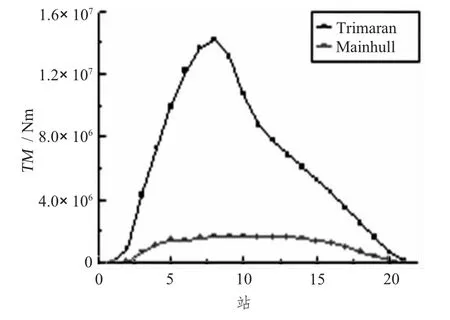
图27 纵向扭矩长期预报Fig.27 The long term of longitudinal torsion
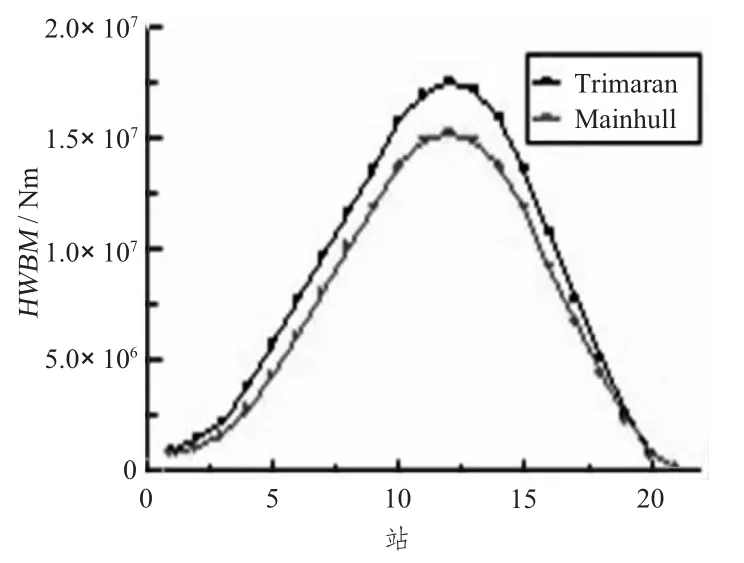
图29 水平弯矩长期预报Fig.29 The long term of horizontal moment
5.4 不同极限有义波高波浪载荷长期预报对比分析
分别采用极限有义波高为6 m和9 m来做长期预报,三体船横纵向波浪载荷长期预报值的变化见图30~图33。横坐标为沿船宽或船长的站号,纵坐标为载荷在极限有义波高为6 m和9 m时的长期预报值,响应是单幅值。其中“6 m Hs limit”代表6 m极限有义波高,“9 m Hs limit”代表9 m极限有义波高。从图中可以看出,二者变化趋势一致,且极限波高值越大,预报值也就越大。

图30 横垂向弯矩长期预报Fig.30 The long term of transverse prying moment
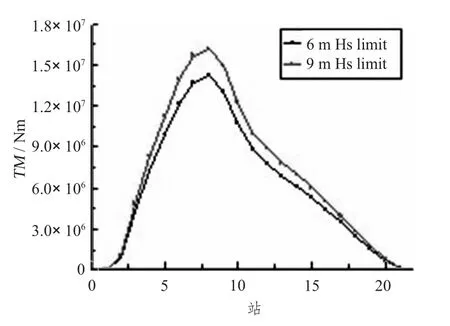
图31 纵向扭矩长期预报Fig.31 The long term of longitudinal torsion

图32 纵垂向弯矩长期预报Fig.32 The long term of longitudinal prying moment

图33 水平弯矩长期预报Fig.33 The long term of horizontal moment
6 结语
本文采用三维频域计算方法对高速三体船波浪载荷进行计算分析并根据IACS推荐的海浪谱及方法给出了长短期预报值。通过对高速三体船横纵向波浪载荷的比较研究,本文得出以下主要结论:
1)横向波浪载荷与纵向波浪载荷都是三体船较为重要的波浪载荷。
2)一般三体船主要横向波浪载荷在横浪时较大、主要纵向波浪载荷在顶浪时较大、而横、纵向扭矩在斜浪时较大,所以在进行结构分析和强度衡准时,应采用不同的载荷工况分别分析计算。
3)就纵向波浪载荷而言,三体船2个较小的片体对纵向扭矩影响较大。而对纵垂向弯矩和水平弯矩影响不大。
4)在相同的海浪统计资料下,采用不同的极限有义波高对长期预报结果也有影响,极限有义波高越大,长期预报值也就越大。
根据本文计算结果,可了解高速三体船的波浪载荷特征,为结构的进一步优化设计提供重要依据,并为相关规范公式的修改提供参考。
[1]LLOYD'S REGISTER(LR).Rules for the clssification of trimarans[S].2006.
[2]汪雪良.波浪中多体船舶响应的二维理论研究[D].中国船舶科学研究中心,2006.
[3]戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社.2008.
[4]马山.高速船舶运动与波浪载荷计算的二维半理论研究[D].哈尔滨工程大学,2005.
[5]戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.
[6]HydroD User's Manual[Z].DNV.2008.
[7]IACS NA Rec.34[Z].IACS.,2001.
