基于粒子群的城市交通信号两级模糊控制

曾松林，余立建，郭翠玲，2

（1.西南交通大学 信息科学与技术学院，四川 成都 610031；2.商丘职业技术学院 机电工程系，河南 商丘 476000）

1 单交叉口几何模型及相位设置

为避免交叉口各向交通流之间的冲突，人们引入了信号灯。在一个信号控制周期内，交叉口上某一支或几支交通流所获得的通行权称为相位。

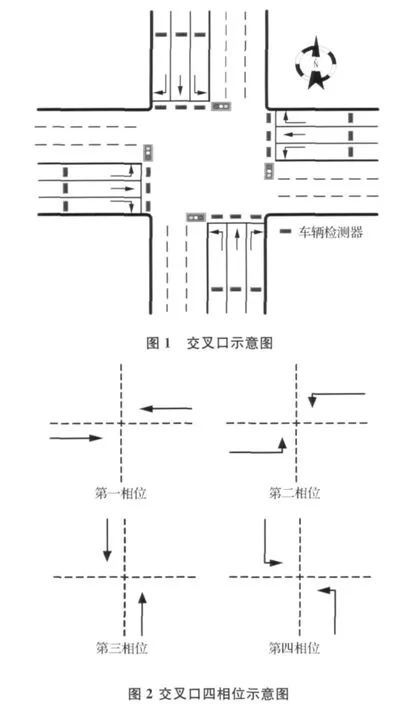
一个典型的四相位交叉口如图1所示，包括东、西、南、北4个通行方向，每个通行方向包括左转、直行和右转3支交通流。本文以此为研究对象，采用东西直行、东西左转、南北直行、南北左转的四相位控制方式，右转车流统一设定为即时放行，在控制中不加以考虑。在每条车道上安装2个检测器构成一个检测区以获取实时交通流信息：一个设在停车线处，用于检测该车道的车辆离开数；另一个设在距停车线一定距离处，用于检测车辆驶入数。

交叉路口四相位控制如图2所示，图中箭头表示该相位车流对应的通行方向，未标出的方向为该相位车流禁止通行的方向。

2 交通信号两级模糊控制策略

2.1 模糊控制算法

一般地，在交通控制中，当车辆排队长度较短时，信号控制周期应短一些，但一般不应小于P×15s（P为相位数），以防止某一方向的绿灯时间小于15s，使车辆来不及通过路口而影响交通安全；当队长较长时，信号周期则应该长一些，但一般不能超过200s，否则，某一相位的红灯时间太长，驾驶员人心理上不能忍受。当排队长度很小时，一般按最小周期运行；当队长很大时，只能按最大周期控制，此时车辆堵塞现象已不可避免。

如上所述，为了有效减小车辆平均延误，两级模糊控制算法设计步骤如下：

Step1：从相位i开始，根据交通状况分别限定各相位的最小绿灯时间Gimin和最大绿灯时间Gimax。

Step2：给获得通行权的相位i赋予最短绿灯时间Gi＝Gimin。

Step3：在当前绿灯相位的绿灯时间结束前，根据车辆检测器检测到的交通信息计算绿灯相位的繁忙度和各红灯相位的紧迫度。

Step4：从当前红灯相位中选择紧迫度最大的相位作为下一个绿灯相位的预备相位。

Step5：以当前绿灯相位的繁忙度和预备相位的紧迫度作为模糊控制器的输入变量，经过模糊推理，得到当前绿灯相位的绿灯延长时间ΔG。

Step6：根据不同的车流情况确定阈值M：

1）若ΔG＞M，且Gi＋ΔG＜Gimax，则Gi＋ΔG→Gi，转Step3。

2）若ΔG＞M，且Gi＋ΔG≥Gimax，则ΔG＝Gimax－Gi，Gimax→Gi，转Step7。

3）若ΔG＜M，则转Step7。

Step7：当前绿灯相位延长ΔGs后切换到下一绿灯相位，转Step2。

2.2 两级模糊控制器设计

两级模糊控制器的结构如图3所示，第一级包括2个模块：红灯相位评估模块和绿灯相位评估模块；第二级包括1个模块：决策模块。每个模块都是1个子模糊控制器。

图3 两级模糊控制系统

2.2.1 红灯相位评估模块

红灯相位评估模块根据当前所有红灯相位的交通状况，计算出当前各红灯相位的紧迫度，并从中选出紧迫度最高的相位，作为下一个绿灯相位的预备相位。该模块的输入为当前各红灯相位上下游检测器之间的车辆数Qr和当前各红灯相位的红灯持续时间Tr，输出为预备相位的紧迫度Ur。若某一相位内包含多支交通流，则通过模糊推理分别计算出该相位各交通流的紧迫度，然后取平均值作为整个相位交通流的紧迫度。

Qr的物理论域为[0，30]，量化因子为0.4，其模糊论域为[0，1，2，…，12]，划分为5个模糊子集，分别为｛很少，少，中等，多，很多｝，简记为｛VF，F，M，E，VE｝。

Tr的物理论域为[0，120]，量化因子为0.2，其模糊论域为[0，1，2，…，24]，划分为5个模糊子集，分别为｛很短，短，中等，长，很长｝，简记为｛VS，S，M，L，VL｝。

Ur的物理论域为[0，1]，比例因子为1，其模糊论域为[0，0.05，0.1，…，1]，划分为5个模糊子集，分别为｛很低，低，中等，高，很高｝，简记为｛VL，L，M，H，VH｝。

输入输出变量的模糊隶属函数如图4所示。

图4 红灯模块输入输出变量的模糊隶属函数

通过总结实践和专家经验，建立了25条模糊控制规则，如表1所示。

表1 红灯模块模糊规则

2.2.2 绿灯相位评估模块

绿灯相位评估模块根据当前绿灯相位的交通信息，计算出该相位的紧迫度。该模块的输入为当前绿灯相位上下游检测器之间的车辆数Qg和当前绿灯相位经过最小绿灯时间后的延长时间Tg，输出为当前绿灯相位的繁忙度Bg。若某个相位包含多支交通流，则取该相位各交通流排队长度的最大值，绿灯延长时间是相同的。

Qg的物理论域为[0，30]，量化因子为0.4，其模糊论域为[0，1，2，…，12]，划分为5个模糊子集，分别为｛很少，少，中等，多，很多｝，简记为｛VF，F，M，E，VE｝。

Tg的物理论域为[0，45]，量化因子为0.4，其模糊论域为[0，1，2，…，18]，划分为5个模糊子集，分别为｛很短，短，中等，长，很长｝，简记为｛VS，S，M，L，VL｝。

Bg的物理论域为[0，1]，比例因子为1，其模糊论域为[0，0.05，0.1，…，1]，划分为5个模糊子集，分别为｛很低，低，中等，高，很高｝，简记为｛VL，L，M，H，VH｝。

输入输出变量的模糊隶属函数如图5所示。

图5 绿灯模块输入输出变量的模糊隶属函数

通过总结实践和专家经验，建立了25条模糊控制规则，如表2所示。

2.2.2 决策模块

决策模块根据预备相位的紧迫度Ur和当前绿灯相位的繁忙度Bg，进而决定延长绿灯时间或切换到下一相位。若能够延时的长度小于5s，则系统在延时结束后立即进行相位切换。

Ur和Bg的模糊子集划分与前面红灯模块和绿灯模块的划分一致，在此不再赘述。决策模块的输出ΔG的物理论域为[0，20]，比例因子为1，其模糊论域为[0，1，2，…，20]，划分为5个模糊子集，分别为｛很短，短，中等，长，很长｝，简记为｛VS，S，M，L，VL｝。输入变量Ur与Bg的模糊隶属函数划分同上。

表2 绿灯模块模糊规则

输出变量的模糊隶属函数如图6所示。通过总结实践和专家经验，建立了25条模糊控制规则，如表3所示。

表3 决策模块模糊规则

图6 决策模块输入输出变量的模糊隶属函数

3 隶属度函数的粒子群优化

粒子群优化算法（Particle Swarm Optimization，PSO），作为群智能（Swarm Intelligence）领域中的一种重要方法，是由Kennedy博士和Eberhart博士通过对鸟群、鱼群和人类社会某些行为的观察研究，于1995年提出的一种基于群体智能的全局随机搜索算法。

在粒子群优化算法中，每个优化问题的潜在解都是搜索空间中的一个粒子。每一次迭代，粒子通过跟踪个体极值pbest和全局极值gbest不断更新自己。

设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子的位置表示为一个D维的向量，记为

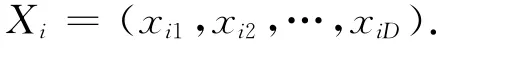
第i个粒子的“飞行”速度也是一个D维的向量，记为

第i个粒子迄今为止搜索到的最优位置称为个体极值，记为

整个粒子群迄今为止搜索到的最优位置为全局极值，记为当找到这些最优值时，粒子根据以下公式不断更新速度和位置

式中：i＝1，2，…，N，d＝1，2，…，D；vid为粒子的速度，vid∈ [－vmax，vmax]，vmax为常数，由用户设定，用来限制粒子的速度；w为非负数，称为惯性因子；c1，c2为学习因子；r1，r2为[0，1]范围内的均匀随机数；iter为当前迭代次数；itermax为最大迭代次数；wmin为惯性因子的下限；wmax为惯性因子的上限。

两级模糊控制器采用分级分块的方法对较多的输入参数进行了处理，有利于更加合理地制定决策规则，但也包含了较多的隶属度函数，若这些参数全部由人工设置，则其合理性难以得到保证。当系统参数固定时，若交通流波动较大，则模糊控制器的性能也会受到相应的影响。如果隶属度函数能随不同的交通状况而自适应地调整，则有利于提高模糊控制器的性能。于是，本文采用粒子群算法对两级模糊控制器的隶属度函数进行了优化。

粒子群算法优化过程：两级模糊控制器首先采用人工初始设置的隶属度函数进行模糊推理，同时历史数据库开始对各时段的交通流数据进行记录。每经过一定的时间间隔，利用历史数据库中的交通流数据进行交通再现模拟，同时，采用粒子群算法对模糊隶属度函数进行寻优，找出适应当前交通状况的模糊隶属度函数，并将其送入模糊控制器加以更新。

粒子群优化控制系统结构如图7所示。

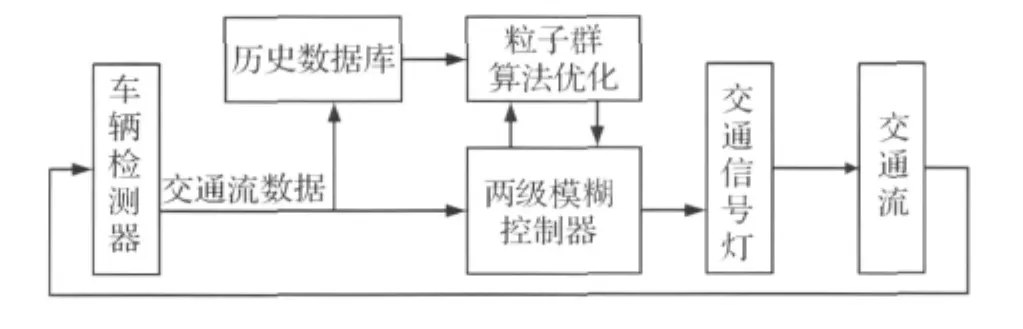
图7 粒子群算法优化的两级模糊控制器

4 仿 真

为了验证两级模糊控制器及其优化的控制效果，用 MATLAB 7.0编写了定时控制、两级模糊控制以及优化仿真程序，以车辆平均延误为性能指标，在相同的交通条件下对定时控制、优化前的两级模糊控制以及优化后的两级模糊控制各进行了10次计算机仿真。仿真参数设置为：假设各方向车辆到达交叉路口是随机的且服从泊松分布，所有车辆都已换算成当量小汽车（PCU），直行相位的车流平均为900PCU／h，左转相位车流平均为720PCU／h；每次仿真时间设置为1200s，在绿灯相位内，车辆以1辆／s的速率离开等候的车队，仿真结果如图8所示。

图8 仿真结果

从仿真结果可以看出，两级模糊控制的结果明显优于定时控制，同时，优化后的两级模糊控制相对于优化前，性能也有所提升。这主要是因为模糊控制能模仿有经验的交警指挥交通时的思路，直接用路口车辆的实时信息进行推理、决策，从而实现交通信号的自适应控制，达到很好的控制效果。而经粒子群优化后的隶属度函数弥补了其完全由人工设置的不足，因此，相对于优化前，车辆的平均延误也有所减少。

5 结束语

由于模糊控制器的模糊规则和隶属度函数都完全由人工确定，带有一定的主观性，因此，本文利用粒子群优化算法对两级模糊控制器的隶属度函数进行了优化，使模糊控制系统能根据不同的交通信息自适应变化，从而更加合理地对多相位或者交通状况复杂的交叉路口进行控制。本文提出的方法具有良好的适应性并可在不同相位设置的路口方便地推广，将其用于城市交叉口的信号控制具有较大的优势。

[1] 许伦辉，衷路生，徐建闽.基于神经网络实现的交叉口多相位模糊逻辑控制[J].系统工程理论与实践，2004（7）：135－140.

[2] Pappis C P，Mamdani E H.A fuzzy logic controller for a traffic junction[J].IEEE Trans on Systems，Man and Cybernetics，1997，SMC－7（10）：707－717.

[3] 刘智勇，朱劲，李秀平，等.单交叉口的多相位模糊控制[J].信息与控制，1999，28（6）：453－458.

[4] 徐冬玲，方建安.交通系统的模糊控制及其神经网络实现[J].信息与控制，1992，21（2）：74－78.

[5] 陈洪，陈森发.单路口交通实时模糊控制的一种方法[J].信息与控制，1997，26（3）：229－233.

[6] 高俊侠，李建更，陈阳舟，等.交通信号2级模糊控制系统的优化设计与仿真[J].北京工业大学学报，2009，35（1）：19－24.

[7] 刘智勇.智能交通控制理论及其应用[M].北京：科学出版社，2003.

[8] 杨祖元，刘鸿飞，杜长海.交通强度优先的交叉口模糊控制研究[J].计算机工程与应用，2009，45（36）：193－195.