斜支撑钢箱梁变形分析

2013-08-22李军卫胡金萍贺文彪

交通科技与经济 2013年5期

陈宇，李晶，李军卫，胡金萍，贺文彪

（黑龙江东方学院建筑工程学部，黑龙江哈尔滨 150086）

1 钢箱梁试验与有限元模拟

1.1 试验模型

荷载试验的作用和目的是通过对桥梁结构的直接加载后进行有关测试、记录与分析，为深入探索提供了科学依据。箱梁桥试验模型是由厚度为4mm的Q235钢板焊成的单室箱梁。三跨连续梁总长为4m，计算跨径1m＋2m＋1m，梁高0.12m，桥面宽 0.272m，加劲肋与横隔板间距0.25m。在箱梁顶面、底面和腹板布置17个测点，如图1所示。在主跨跨中和1／4、1／8、3／8截面处以及边跨跨中都布置了测点。试验采用油压千斤顶对试件主跨跨中分级加载，利用YJ 225静态电阻应变仪测定应变值。将百分表对称布置在计算截面，观测箱梁加载时的挠度变化。试验建立了0°、15°、30°、45°共4种不同斜交角的支座支撑条件。

1.2 有限元模拟

利用ABAQUS的壳单元模拟钢箱梁截面。特殊用途壳单元分为两类：薄壳单元和厚壳单元。当厚度和跨度比小于1／15时，可以忽略壳体的横向剪切变形，认为是薄壳问题，即垂直于壳中面的平面在变形中应保持垂直于壳中面。模型的钢板厚度仅为4mm，且梁体以受弯为主，钢板在变形中横向剪切变形的影响极小，属于薄壳问题。本文采用壳单元S4R5模拟钢板，实体单元C3D8模拟支座的垫条。为避免对塑性材料直接施加点荷载或集中力，施加荷载时，集中力施加在与顶板建立耦合约束的参考点上。计算时计入几何非线性和材料非线性，几何非线性问题的模拟只需在前处理分析中设定几何非线性的分析项即可实现，材料非线性问题的模拟利用低碳钢应力－应变曲线数值为被测对象的名义应力和名义应变。

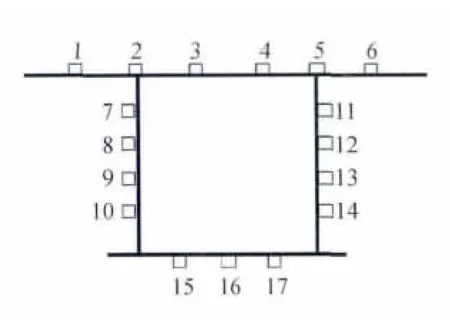
图1 测点布置

1.3 试验成果与有限元计算对比

斜率为0°、15°、30°、45°的情况下，在主跨跨中桥面中心的集中力作用下的挠度和底板应变计算结果如表1所示。从试验数据与有限元计算结果来看，ABAQUS的薄壳单元和通过改变支撑方向的支座实体单元可以很好的模拟钢箱梁斜桥的静力学行为，有限元计算结果与试验数据吻合较好。

2 挠曲变形分析

2.1 箱梁变形特点

根据现有的箱梁研究成果，参考文献[12]关于正桥的变形问题，箱梁的变形主要有：纵向弯曲变形、刚性扭转、畸变和横向翘曲，如图2所示。

2.2 斜支撑箱梁变形分析

有限元计算的整体坐标系为：X轴是梁的横向方向；Y轴是箱梁顶板的法线方向；Z轴是梁的纵向方向。图3中各图左侧为边支点截面，右侧为主跨跨中截面。

图2 箱梁变形状态

桥梁钢结构设计采用的容许应力法，外力的效应值不得大于结构抗力的容许应力，容许应力是钢材的名义屈服点除以安全系数，该安全系数通常取1.7～2.5。可知容许应力法保证了钢结构在使用阶段基本处于弹性工作状态。有限元计算结果表明，在集中力25kN的中心荷载作用下，跨中附近箱梁底板和顶板应力较小，主跨最大挠度2.9mm，美国钢结构建筑与桥梁设计标准中挠度准则规定的钢梁挠度限值为计算跨径的1／800，连续钢箱梁处于弹性工作状态。由图3（a）、（b）、（c）、（d）可以看出15°和30°斜率下相同横断面上的节点位移离散程度很小，截面转动微小。由图3（e）、（f）可以看出45°斜率下边跨跨中区域的横断面节点竖向位移离散程度较大，横断面绕Z轴发生转动，即扭转；靠近斜支撑区域的横断面节点纵向位移也有一定程度的离散，横断面绕Y轴发生转动。

图4中的横向坐标对应的箱梁位置为：1为靠近主跨支点；2为主跨1／8截面处；3为主跨1／4截面处；4为主跨3／8截面处；5为主跨1／2截面处。偏心荷载的偏心距为40mm。由图4可以看出，斜率为15°时与正桥相比挠度十分接近，最大偏差仅为10%；斜率为30°与45°的挠度较为接近，最大偏差为14.3%；挠度偏差随着斜率增大而增大，斜率超过15°后挠度值随斜率的增大而减小，斜率为45°时与正桥相比的最大偏差为38.5%。