基于VISSIM仿真的平面交叉口信号配时方案比选分析
2013-08-22安慧姝王占宇吕岩峰
张 鹏,赵 静,安慧姝,王占宇,吕岩峰
(1.黑龙江工程学院 汽车与交通工程学院,黑龙江 哈尔滨 150050;2.哈尔滨德强商务学院,黑龙江 哈尔滨 150000;3东北林业大学 交通学院,黑龙江 哈尔滨 150040)
随着经济的发展和城市化水平的提高,城市交通问题日益突出。如何充分利用现有道路资源,通过科学合理的交通控制手段,最大限度的提高信号交叉口的通过能力、降低延迟时间一直是交通工程领域重要的研究课题。在诸多交通控制手段中,优化信号配时是最直接有效的方法之一,而应用交通仿真软件进行配时研究是未来发展的方向。针对信号交叉口的信号配时算法软件有TRANSYT系统、SCATS系统和SCOOT系统,以及力加拿大开发的GreenStar“绿星”软件,GreenStar是为实现道路双向交通绿波控制而开发的。
目前,信号配时的模型也越来越多,每种模型都有其各自的优缺点,应用合适的模型进行信号配时方案的合理设计可以解决道路交通高峰拥堵的重要措施。在对交叉口进行调查和数据分析的基础上,通过VISSIM仿真对国内外的配时主要模型进行研究分析,选出适合我国城市交通流特点的模型,对于改善城市道路交通拥堵状况、提高道路通行能力、减少交通事故具有十分重要的现实意义。
1 常见配时模型分析
目前,国内外常见的交叉口信号配时模型主要有4种,包括国内的上海市综合算法,美国的HCM算法,英国的韦伯斯特算法以及澳大利亚配时方法。各种配时模型的绿信比、流量比、损失时间、各相位有效绿灯时间等基本配时参数的计算公式一样,只有周期时长、延误计算公式会由于应用范围的不同而不同,本文仅通过延误和周期时长这两个参数对各种配时模型做简单介绍。
1.1 韦伯斯特配时方法
该配时方法和计算公式首先由韦伯斯特和柯布在20世纪50年代提出,后经过R·金伯等人改进而来。它的延误公式是通过蒙特卡罗模拟法对随机延误和平均延误进行标定得到,如下式
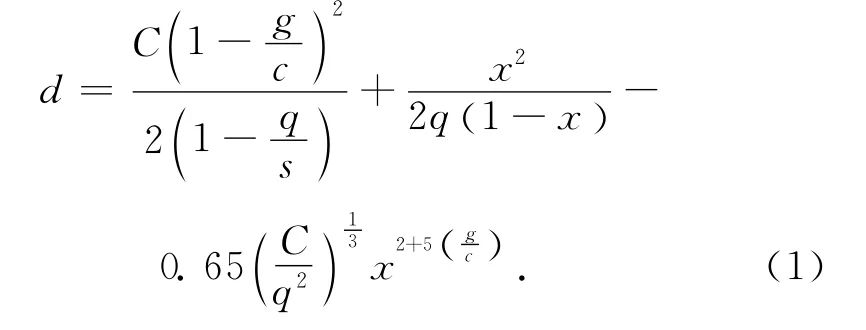
式中:d为每辆车的平均延误,s;c为周期时长,s;g为有效绿灯时间,s;x为饱和度,s;q为到达率,veh/s。
为了得到使交叉口总延误达到最小的最佳周期时长,将总延误D对C求偏导,并令偏导数为0,可得到最佳周期时长

式中:C0为最佳周期长度,s;L为总的损失时间,s;Y为所有相位关键车流的流量比之和。
该模型较好地反映了交叉口在低饱和情况下,车辆延误与信号配时、交通量大小、饱和度间的定量关系。但当交叉口上的实际交通量很小时,信号周期若设置过短,对行车安全是不利的。因此,通常要规定一个最短信号周期的限值,参考西方国家一般为25s。
而当交通量过大,造成设置周期过长,则车辆延误时间会骤然急速增长,反而会造成交通拥挤,应将120s视作最佳周期的上限值,但在多相位及饱和交通流情况下常常突破该上限。
1.2 澳大利亚ARRB配时方法
韦伯斯特模型结构简单、使用方便,是目前应用最普遍的一种模型,不足之处是当饱和度越接近1时,计算的延误越不准确,更无法计算超饱和交通情况下的延误。ARRB法考虑了超饱和交通情况,将延误公式改为
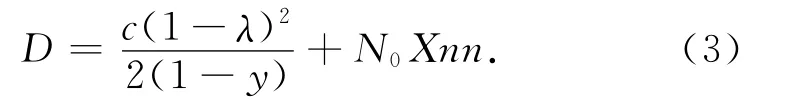
同时,再考虑停车因素,完全停车的停车率

式中:N0为溢流排队长度。
再把优化周期时间的指标改为油耗,而把油耗作为延误与停车的函数,即油耗
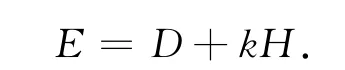
式中:E为油耗;H为每小时完全停车数,H=hq;k为停车补偿系数。
可按不同优化要求,取不同的值。要求油耗最小时,取k=0.4;消费(包括延误、时间损失等)最小时,取k=0.2;延误最小时,取k=0。则最佳周期时长公式为
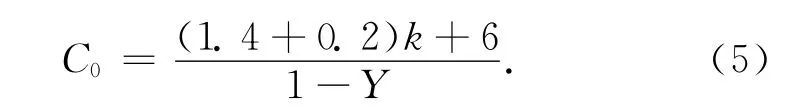
1.3 美国HCM法
该模型是基于美国道路通行能力手册2000版(HCM2000)延误模型的基础上进行的配时方法。信号控制交叉口最佳周期时长估算公式为
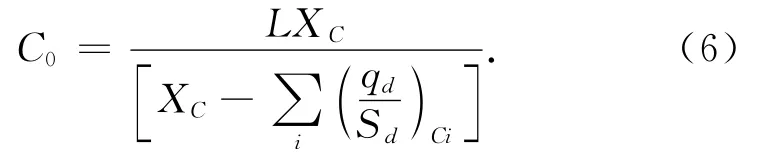
式中:XC为交叉口的关键v/c比;qd为设计交通量,pcu/h;Sd为设计饱和流量,pcu/h。
在美国HCM法中,计算结果表明,当计算周期介于30~90时,可取信号周期为最靠近5的整数倍;当周期超过90s时,则取最靠近10的整数倍。美国HCM算法配时的延误计算与上海市综合算法的延误计算相同。
1.4 上海市综合算法
上海市综合算法是在综合研究英国、澳大利亚和美国等国家以及我国现有配时方法的基础上,结合我国交通特点,讨论定时信号的配时基本方法。通过计算各进口道的设计小时交通量和饱和流量计算其最佳周期,公式为

周期时长应该取40~180s,高峰期间应不大于120s,延误是交叉口各进口道的每车平均信控延误;进口道每车平均延误是进口道各车道延误的加权平均值;整个交叉口的每车平均延误是各进口道延误加权平均值。
各个进口道的平均信控延误,按该进口道中各车道延误的加权平均数估算

式中:dA为进口道A的平均信控延误;di为进口道A中第i车道的平均信控延误;qi为进口道A中第i车道的小时交通量,换算为高峰15min时的交通流率,辆/15min。
整个交叉口的平均信控延误,按该交叉口中各进口道延误的加权数估算
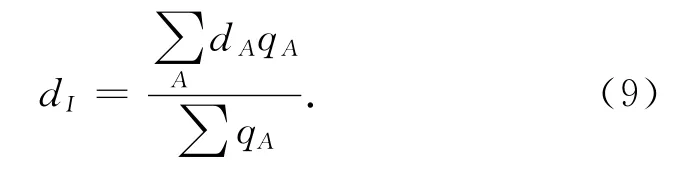
式中:dI为交叉口每车的平均信控延误;qA为进口道A的高峰15min交通流率,辆/15min。
2 实例分析
2.1 交通调查
以哈尔滨市红旗大街与辽河路交叉口为研究对象,该交叉口是三相位交叉口,表1为相位配时表,表2为交通量数据,表3为点样本法延误调查及计算结果。

表1 红旗大街与辽河路现有三相位配时表s
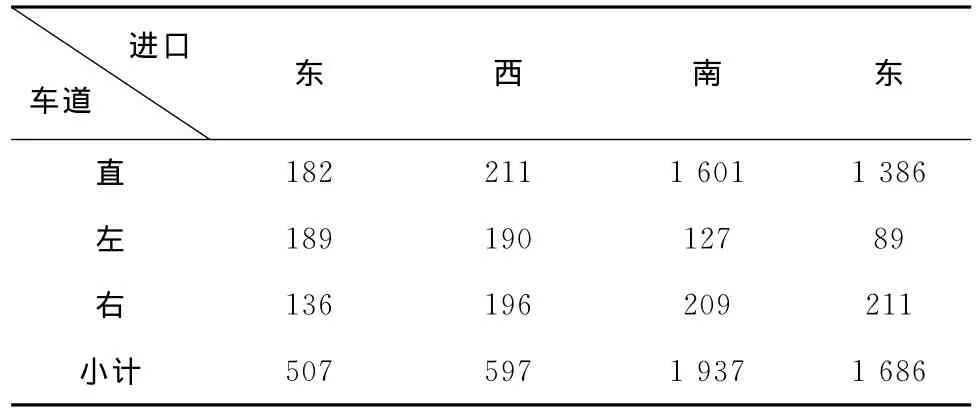
表2 红旗大街与辽河路交叉口进口道交通量调查表 辆
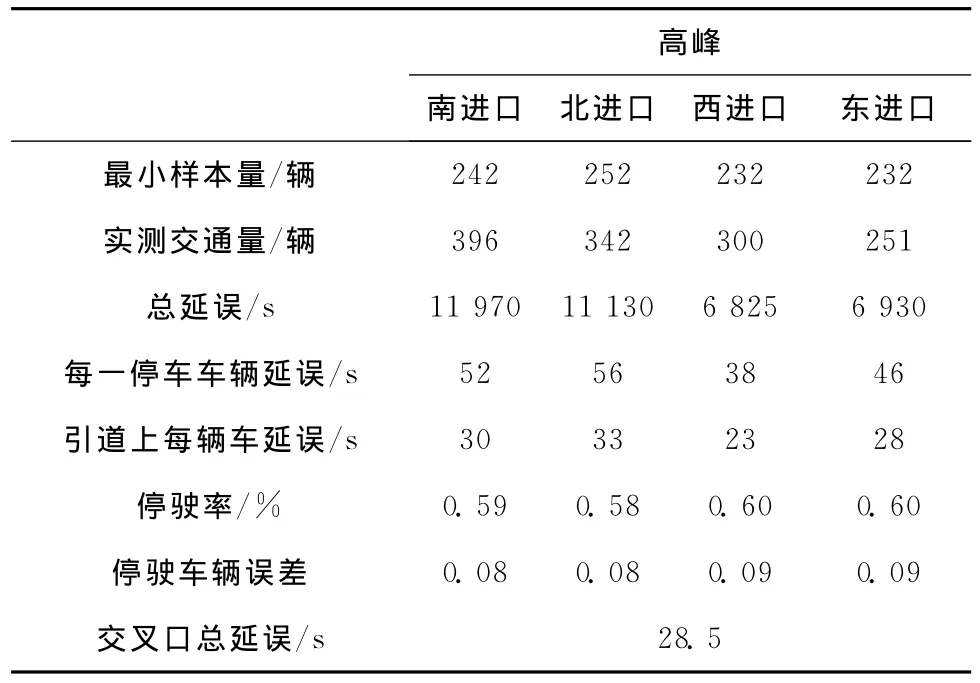
表3 红旗大街与辽河路交叉口延误调查及计算结果表
2.2 各种方法进行配时
根据表2和表3数据,根据式(2)、式(5)、式(6)、式(7)和各自的饱和流量计算公式得出相应的配时结果,见表4~表7。

表4 韦伯斯特算法配时三相位配时表s

表5 美国HCM法配时三相位配时表s

表6 澳大利亚算法配时三相位配时表s
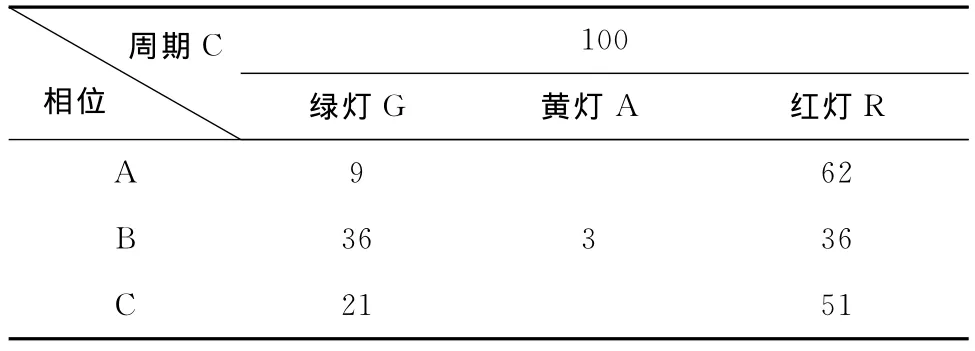
表7 上海市综合算法配时三相位配时表s
3 基于VISSIM仿真配时研究
VISSIM可作为许多交通问题分析的有力工具,在交通控制领域可以对固定式信号灯进行配时方法的开发、评价及优化,对各种类型的信号控制进行模拟,还可以通过外部信号发生器来进行模拟交通信号配时策略,允许用户设计自己定义的信号控制方法等。
3.1 VISSIM 仿真
利用该功能对信号配时方案进行研究,将测得的原始数据包括每条车道的交通量、车道宽度、大车比率、每条车道的功能一一导入VISSIM软件,由于配时中并没有改变每条车道的功能和加减相位,所以分别输入4种配时方法,周期得出延误。以韦伯斯特算法为例,它的仿真延误见图1。
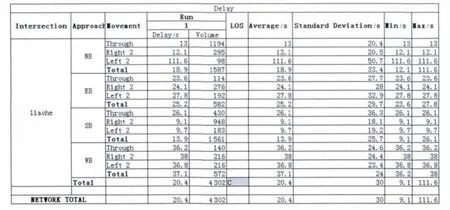
图1 韦伯斯特算法配时仿真的延误
3.2 最优模型选取
从配时公式上看,上海市综合算法与美国HCM算法类似,设计饱和流量的计算方法相同且具有相同的延误计算,可以轻易的看出上海市综合算法是从美国HCM算法衍生出来的,只不过是上海市综合算法配时选取的是最短的配时周期,而美国HCM算法则引入了另一个参数XC(交叉口的关键v/c比),XC是对整个交叉口而言。关键车道组是指对给定的信号相位,具有最高流率比的车道组,例如一个二相位信号中,在同一绿灯时间对象车道组需要更多的时间(即具有较高的流率)。需要时间较多的车道组就是该相位的关键车道组(来确定该相位所需绿灯时间)。XC值范围从1.00~0.00。美国HCM法配时中不能大于1.00也不能等于Y(组成周期的全部信号相位的最大流量比),由此可以看出XC在Y与1.00中选取,这样美国HCM法配时之后得出的周期是在一定的范围之内的,少了上海市综合算法的局限性。
通过上面的计算实例及VISSIM仿真结果进行比较分析,见表8和图2。

表8 4种配时方法比较
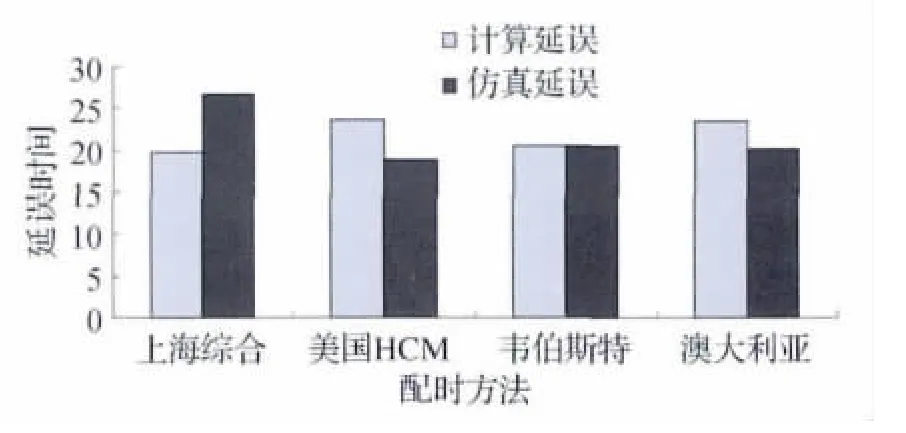
图2 各种配时方法计算延误与仿真延误比较分析
韦伯斯特算法与澳大利亚算法公式也很类似,澳大利亚算法是从韦伯斯特算法改进而来的,它们的设计饱和流量计算相同,只考虑车道是否靠边、车道宽度、坡度、转弯半径和转弯车辆所占比例。不同的是澳大利亚算法中引入了k值,当k=0时延误最小,此时与韦伯斯特算法最接近,它们的延误计算也略有不同,澳大利亚算法引入了溢流排队长度的延误,替代了韦伯斯特延误公式中的随机到达延误和计算机仿真延误。
从设计饱和流量上看,上海市综合算法和美国HCM算法的设计饱和流量比韦伯斯特算法和澳大利亚算法要精确的多,前两者对设计饱和流量修正的更加全面完善,考虑了行人或自行车影响校正系数和有无专用相位。可以得出上海市综合算法和美国HCM算法要优于韦伯斯特算法和澳大利亚算法。
综上以及计算结果表明上海市综合算法周期时长最短,从计算的延误看,上海市的延误19.8s也是最小的,但从仿真中可以看出上海市算法却是最大的,可知该算法的延误计算公式有着很大的误差。在仿真中,美国HCM算法的延误时最小且与该方法对应的延误计算结果相近。韦伯斯特算法与澳大利亚算法的延误计算虽然与仿真中数据相接近,但仿真结果却没有美国HCM算法配时的延误小,从而可以得出最优配时模型是美国HCM算法。
4 结束语
城市交通是整个交通系统中最为关键和重要的部分,而城市交通信号控制系统是实施智能交通系统工程的首要任务。本文应用4种配时模型对实际交叉口配时,应用VISSIM软件比较分析各种配时方法的优缺点,对各交叉口选用合理的配时方法,对解决交通拥挤问题有实际意义。
[1] 顾宝华.城市道路交又口信号配时设计方法研究[D].西安:西北工业大学,2005.
[2] 范东凯,胡晓明.VISSIM在信号交叉口配时优化中的应用 [J].中外公路,2011,31(5),257-259.
[3] 盖学松.信号控制交叉口周期时长对饱和 .流量的影响研究[D].上海:同济大学,2007.
[4] 潘云伟.交通信号配时优化仿真评价技术研究[D].昆明:昆明理工大学,2011.
[5] 刘瑞婷.城市平面正交交叉口信号配时模型研究 [D].南京:南京林业大学,2008.
[6] 蒋金勇,云美萍,杨佩昆.基于HCM 2000延误模型的最佳周期时长估算公式 [J].同济大学学报,2009,37(8):1024-1028
[7] 武连港,沙尧尧,李标.城市主干路协调配时实证[J].交通科技与经济,2012,14(14):102-106.
[8] 李 林,徐建闽,黄思博,陈元朵.VISSIM在信号交叉口优化中的应用 [J].现代交通技术,2009,6(5),62-64.
[9] 邓明君,艾瑶,谭德坤.基于仿真的单点交叉口固定信号配时分析 [J].交通科技与经济,2010,12(1):28-31.
