基于角度度量法的混纺纤维定量检测

梁梅，姚志湘，粟晖

（广西科技大学生物与化学工程学院，广西柳州 545006）

目前纺织纤维的一些定量检测方法［1］都需要选用适当溶剂将其中一种或几种纤维溶解，这种检测耗时且实验过程中会产生有毒污染物［2］，无法满足纺织品生产过程中质量监控及国际贸易快速通关检测的需求。近红外光谱（NIR）分析技术在20世纪90年代初得到迅速发展［3］，主要用于快速定量分析和判别分析。NIR分析技术通过所采集的光谱数据对样品进行分析，其特点是准确、快速、无损、无污染并且操作简便［4］。传统的多组分混合体系光谱定量方法是光谱强度结合化学计量学的分析方法，如用偏最小二乘法法（partial least squares，PLS）［5］直接对光谱强度和其对应的物质含量进行多变量回归建立校正模型。传统的光谱结合化学计量学的定量方法由于光强度、测量环境以及样本均匀性等因素引起的信号强度不稳定使非接触分析在过程分析中遇到了很大的障碍［6–8］。近年来研究人员开始运用近红外光谱来检测混纺纤维含量［9–11］，采用偏最小二乘法（PLS）建立被测纤维含量与近红外光谱数据的定量校正模型。该方法对实验环境等要求较高，测量环境以及样本均匀性等因素容易引起信号强度不稳定导致计算不准确。

笔者采用“基于角度度量的多变量分析方法”对混纺纤维组分进行定量分析，探讨角度度量法在混纺纤维含量预测中的应用。

1 原理和方法

1.1 原理

在混合体系中，每个组分可对应为单一向量，体系为多个向量构成的空间。空间也可描述成被测组分向量a和不含该向量的超平面B，体系中包含被测组分和其它组分的被测样本s可表示成介于被测组分向量和超平面间的一个向量，如图1所示，a和s张成的平面与B交于b。

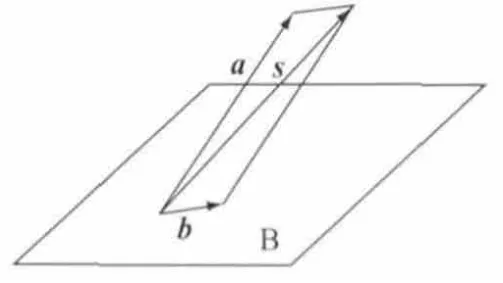
图1 被测组分a、超平面B、待测样本s关系图

向量的长度代表被测物的响应强度，由于体系已经确定，所以a与b的夹角确定，s存在于a和b之间，体系中被测组分a的含量越低，被测样本s与a的夹角θ就越大，反之就越小，见图2。

图2 被测组分a与待测样本夹角关系图

设θi是空间中s与第i个组分向量的夹角，体系中组分含量恒为正值，θ的取值范围是0～π/2，矩阵θ与组分含量Q的关系可用多元体系化学计量学的普遍表达式表示［12］：

式中：θ——混合向量与纯组分向量的夹角；

B——系数；

Q——各组分在总组成中的含量；

ε——随机误差和非线性误差。

基于角度度量的多变量分析方法就是把测量信号的强度度量值转化成被测组分和待测样本的角度度量值进行多变量回归完成定量分析［13］。

1.2 数据处理方法

数据分析步骤如下：

(1)选取建模样本S，S中被测组分a的含量需已知。

(2)通过近红外光谱仪获取建模样本S的多点强度值和被测组分a的多点强度值。

(3)将测量点分割成n个区间，则被测组分a的多点强度测量值被分割为{a1，……，ai，……，an}；建模样本S的多点强度测量值被分割为{s1，……，si，……，sn}。

(4)求取建模样本S和a的角度度量值{θ1，……，θi，……，θn}。

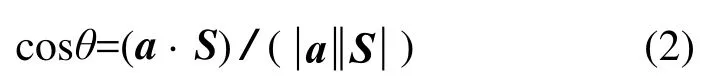
(5)以建模样本S中被测组分a的含量作为因变量，将建模样本S和被测组分a的角度度量值构成的矩阵作为自变量，采用偏最小二乘回归方法(PLS)建立回归模型。

(6)选取预测样本P，通过近红外光谱仪获取P的多点强度测量值，求取样本P和a的角度度量值，将该角度值代入已经建立的模型中，即可预测样本P中组分a的含量。

2 实验部分

2.1 主要仪器与原料

电子分析天平：AR124CN型，上海奥豪斯仪器公司；

近红外光谱仪：Frontier型，附带积分球，美国PE公司；

维纶、腈纶：实验室提供。

2.2 样本制备和近红外光谱采集

维纶和腈纶质量百分数在12%～88%范围内按不同的质量百分比混合配制27个校正集样品，10个预测集样品。

近红外光谱扫描波数范围4 000～10 000 cm–1。扫描混纺纤维样本的校正集、预测集，以及维纶，腈纶两种纯组分的近红外光谱数据。每个样本扫描3次，取其平均值。

3 结果与讨论

选取4 000～6 000 cm–1波段进行分析，图 3为维纶和腈纶的近红外光谱图，图4是维纶和腈纶混合纤维近红外光谱图。

图3 纯纤维光谱图图

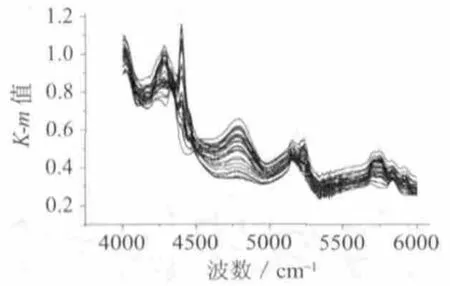
图4 混合纤维光谱图

对光谱进行15点平滑后，直接用偏最小二乘法（PLS）和角度度量法对预测集中的各组分预测结果进行对比，如表1所示。

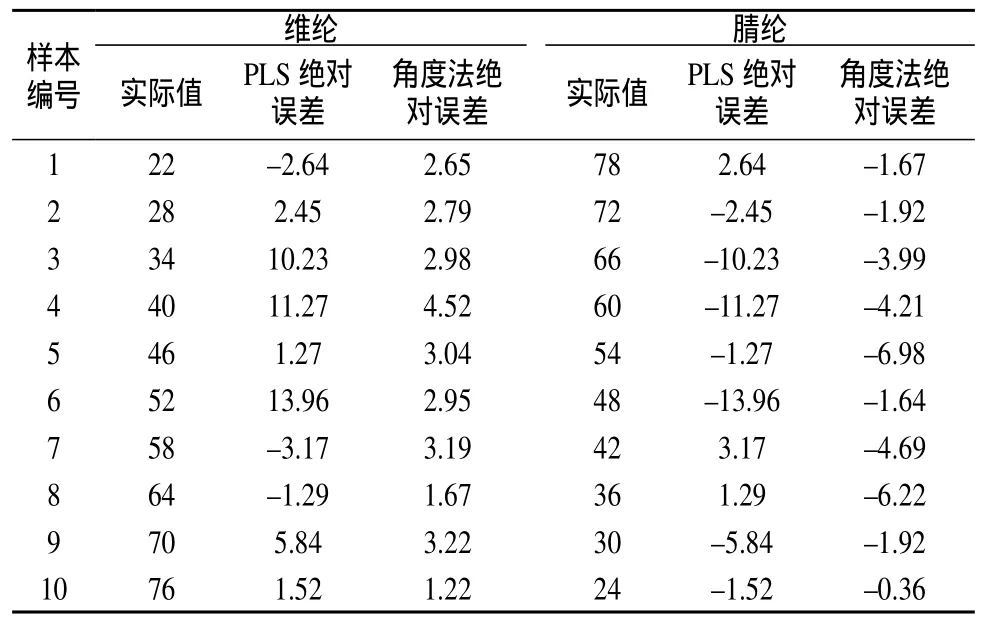
表1 PLS法和角度度量法对预测集中维纶、腈纶预测结果 %

由表1可知，PLS法的预测绝对误差有几个样本超过10%，角度度量法对维纶预测绝对误差在±4.6%以内，对腈纶预测绝对误差在±7%以内。

直接用PLS对近红外光谱进行建模，维纶和腈纶预测值与实际值的线性相关系数r均为0.945 7，标准偏差是6.090 6，均方根误差为6.994 8。角度度量法对维纶预测值与实际值的线性相关系数r为0.999 0，标准偏差为0.892 9，均方根误差为2.189 6；对腈纶预测值与实际值的线性关系r是0.992 8，标准偏差是2.189 6，均方根误差为3.949 3。结果显著改善。两种方法预测值与实际值的线性关系图如图5、图6所示。

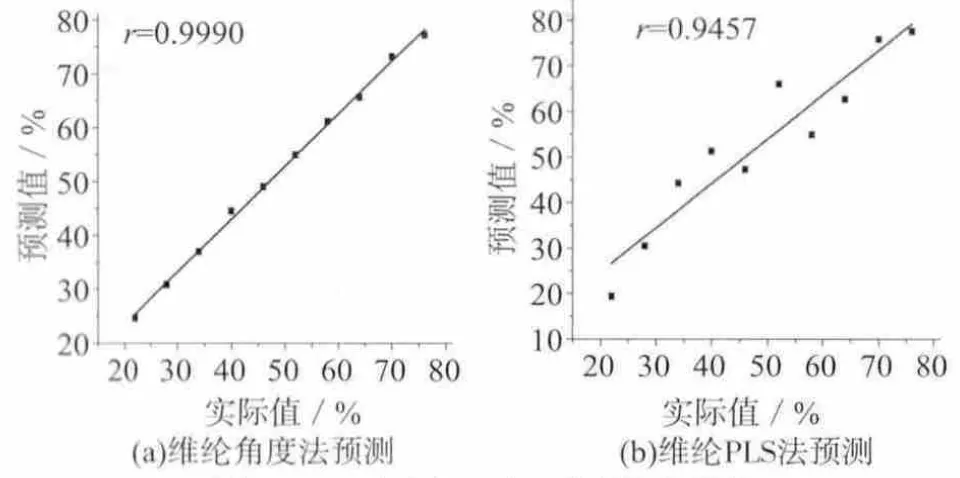
图5 PLS法和角度法对维纶预测结果

两种方法都能表达混纺纤维的定量关系，但PLS法预测绝对误差比角度度量法大，预测模型的稳健性不如角度度量法，因此角度度量法能够完成混纺纤维的定量分析。

4 结论

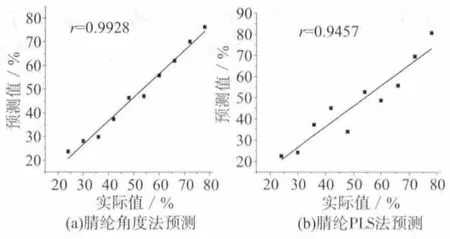
图6 PLS法和角度法对腈纶预测结果

基于角度度量的多变量方法在仪器噪声和环境等因素影响下完成对混纺纤维中待测组分的定量分析，结果满意。因此基于角度度量法能够弥补传统的化学计量学方法在测量强度不稳定时不能对多组分混合体系定量分析的缺点，降低了测量条件对光谱定量分析的要求。

［1］李青山.纺织纤维鉴别手册［M］.2版.北京：中国纺织出版社，2003: 303–305.

［2］尤克非.常见纺织纤维的鉴别方法［J］.教学与研究，1995，(Z2):15–18.

［3］陆婉珍，袁洪福.现代近红外光谱分析技术［M］.北京: 中国石化出版社，2006: 1–2.

［4］严衍禄，赵龙莲，韩东海,等.近红外光谱分析基础与应用［M］.北京: 中国轻工业出版社，2004.

［5］许禄，邵学广.化学计量学［M］.北京: 科学出版社，2004:179–181.

［6］Wayne W Blaser, Robert A Bredeweg, Richard S harner. Process Analytical Chemistry［J］. Analytical Chemistry，1995，67(12):47–70.

［7］Workman J， Koch M，Veltkamp D. Process analytical chemistry［J］.Analytical Chemistry，2007，79(12): 4 345–4 364.

［8］Workman J， Koch M， Lavine B. Process analytical chemistry［J］.Analytical Chemistry，2009，81(12): 4 623–4 643.

［9］桂家祥，耿响，要磊，等.基于近红外光谱法的棉/涤混纺织物中棉含量快速检测［J］.纺织学报，2012，33(4): 55–59.

［10］吕丹，于婵，赵国.利用近红外光谱进行羊绒与羊毛的鉴别技术研究［A］.北京服装学院学报，2010，30(2): 29–34.

［11］王京力，耿响，桂家祥，等.近红外光谱分析技术快速检测锦纶/氨纶混纺织物纤维含量的研究［J］.化纤与纺织技术，2013(2): 42–47.

［12］姚志湘，粟晖.多元统计描述中随机误差与变量空间角的关系［J］.中国科学：化学，2010，40(10): 1 564–1 570.

［13］姚志湘，粟晖.基于角度度量的多变量分析方法：中国，201110188187［ P］.2011–07–06.