基于性能的抗震结构的失效概率
2013-08-22王作君于俊豪
王作君 张 磊 于俊豪
(1.烟台市政府投资工程建设管理办公室,山东烟台 264001;2.山东同舟工程咨询有限公司,山东烟台 264001)
0 引言
合理的设防标准应寻求在地震作用下的损失和抗震投入之间取得最佳平衡,这是一个优化的问题。按照《国际标准ISO 2394∶1998》中的有关内容,最优设防烈度的优化决策模型为使结构全寿命预期总费用趋于最小[1]:

其中,Cb为结构造价;Cm为维护和拆除的预期费用;Pf为寿命期内的失效概率;Cf为失效损失。
附加约束条件[2]:地震后伤亡人数≤社会可接受的水平。
由式(1)可知,优化的一个关键量是寿命期内的失效概率Pf。结构的失效概率主要有两方面的影响因素:1)结构本身的抗震性能,它是设防烈度Id的函数;2)地震本身的危险性,可以根据地震烈度区划图及地震危险性曲线来确定。由此,本文参照文献[7]提出的地震烈度的概率模型和结构的性能目标,来确定我国不同地震危险性分区内,在不同基本烈度下,抗震结构失效概率同设防烈度Id的关系,从而为最优设防烈度的优化提供参考。
1 抗震结构的性能目标
1.1 三水准抗震设防标准
GB 20011-2008建筑抗震设计规范对建筑的抗震设防提出三个水准的要求:小震不坏,中震可修,大震不倒。同时还给出了三个水准烈度的相对关系(见表1)。其中,将众值烈度作为小震,基本烈度作为中震,罕遇烈度作为大震。结构设计中,将基本烈度作为本地区的设防烈度。

表1 三水准抗震设防标准
《建筑抗震设计规范》中给出的“小震”和“大震”分别与基本烈度差1.55度和1度,这两个固定值实际上是忽略了全国各地地震危险性的差异。
而在CECS 160∶2004建筑工程抗震性态设计通则中[4],根据地域差异将全国分为三个区,每个分区内“小震”“大震”与“中震”的烈度差不同,如表2所示,这一概念为基于性能的抗震设计提供了更合理的参考。

表2 不同地震危险性特征区内“小震”“大震”与“中震”的烈度差
另外,《建筑抗震设计规范》中所谓“小震”和“大震”是以基本烈度为参考的,一般以某一特定地区为对象。而基于性能的抗震设计是以特定结构为对象,其最优设防烈度并不一定为该地区的基本烈度,因此以设防烈度Id代替基本烈度来确定“小震”和“大震”更有实际意义。例如,对设防烈度为Id=9度的结构,7度是小震,要求不坏;而对Id=6度的结构,7度是大震,要求不倒。
1.2 抗震结构的五级工作模式
按照我国实际工程震害分析的习惯,将结构破坏程度划分为基本完好B1、轻微破坏B2、中等破坏B3、严重破坏 B4及倒塌B5五个等级。按规范标准,小震不坏应指结构处于“基本完好”(B1)状态,中震可修大致相当于“中等破坏”(B3),大震不倒应指出现“严重破坏”(B4)状态。
文献[3]中给出了抗震结构的五级工作模式(见表3),并定义了结构可能遭遇的各种烈度与设防烈度的关系。


表3 抗震结构的五级工作模式
由此可将抗震结构的各级性能目标表示为设防烈度Id的单值函数,从而可以确定影响结构失效概率的第一个因素。
当然,随着经验的积累,表3中各烈度的定义是可以调整的。而且根据表2中的内容,各烈度同设防烈度的关系应该有地域差异。但是关于这方面的研究还很少,本文暂且采用文献[3]中的定义。
2 设计基准期内地震烈度的概率模型
文献[2]对高小旺等人[7]提出的地震烈度概率模型进行了进一步的研究,以烈度概率分布曲线的形状参数k作为表征不同地区地震危险性差异的特征参数,通过对遍及全国和周边地区的6 376个点的地震危险性特征参数k值的分析,可将全国分为Ⅰ,Ⅱ,Ⅲ三个区并编制了中国地震危险性特征区划图。提出烈度I的地震危险性曲线为:

其中,P为设计基准期内地震烈度的超越概率。将式(3)写为式(4):
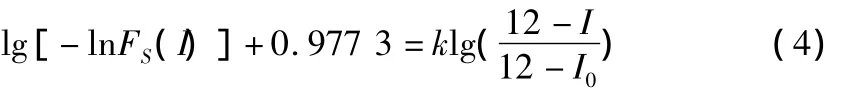
其中,FS(I)为设计基准期内地震烈度的概率分布函数;k为形状参数,Ⅰ,Ⅱ,Ⅲ区的形状参数分别为k=6,10,20;I0为超越概率10%对应的基本烈度。
由上我们可以得到影响结构失效概率的第二个因素。
3 设计基准期内结构的失效概率
由表3和式(2)给出的结构性能目标同设防烈度的关系,以及式(4)给出的地震危险性曲线,可以计算得到发生各种破坏状态 Bi(i=1,2,3,4,5)的概率(即结构失效概率)。

由于地震危险性曲线对不同危险性分区的形状参数k不同,我们将每个分区下结构发生各种破坏状态的概率分别列于表4~表6中。
从表中可以看出,对于某一特定基本烈度I0,设防烈度Id越高,发生高级破坏的概率越小,即危险性越小;对于某一特定设防烈度Id,基本烈度越大,发生高级破坏的概率越大,即危险性越大,这与实际情况相符。
于是,当结构的使用功能、空间布局、结构选型、建筑材料决定后,结构造价、维修和拆除费用,失效损失期望值都是该结构设防烈度Id的函数,把Cm和Cf统一考虑,这时可把式(1)写成:
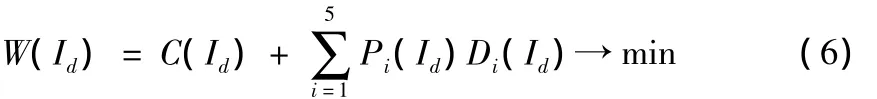
其中,Pi=P(Bi)即发生Bi破坏的概率,Di即Bi级破坏造成的损失,包括维修费、修复费和拆除费。P(Bi)可以从表4~表6中查出。
4 结语
1)本文结合我国现行的建筑抗震规范,重新给出了“小震”“中震”和“大震”的定义,使结构设计真正符合其性能目标的定义。
2)本文将抗震结构的五级工作模式作为基本性能目标,通过地震危险性分析,估算出了我国不同地震危险性分区内,结构在不同设防烈度下的失效概率,为最优设防烈度的决策提供了切实可行的参考。

表4 Ⅰ区结构发生各种破坏状态的概率

表5 Ⅱ区结构发生各种破坏状态的概率
3)本文所给出的失效概率表能直观的表现出结构的失效概率同结构自身抗震能力(设防烈度)和地震危险性(基本烈度)的关系。在设防烈度的优化过程中,我们可以直接查表确定结构的失效概率。

表6 Ⅲ区结构发生各种破坏状态的概率
4)当然,关于五级工作模式所遭遇地震与设防烈度的关系,我们还需要进一步的研究,考虑各地区风险地震风险水平的差异,应针对不同地区给出差值。
[1] International Standard,ISO 2394,General Principles on reliability for structures,Second edition,1998-16-01.
[2] 谢礼立,马玉宏.基于抗震性态的设防标准研究[J].地震学报,2002,24(2):200-209.
[3] 王光远.抗震结构全寿命预期总费用最小优化设计[J].土木工程学报,2003,36(6):1-6.
[4] CECS 160∶2004,建筑工程抗震性态设计通则(试用)[S].
[5] 王光远,邵卓民.抗震结构的最优设防烈度与可靠度[M].北京:科学出版社,1999.
[6] 高小旺.工程抗震设防标准的若干问题[A].城市与工程减灾基础研究论文集[C].北京:中国科学技术出版社,1996.
[7] 高小旺.不同重要性建筑抗震设防标准的探讨[A].城市与工程减灾基础研究论文集[C].中国地震局工程力学研究所,2000.
[8] 马玉宏.基于性态的抗震设防标准的研究[D].北京:中国地震局工程力学研究所博士学位论文,2000.
[9] 马玉宏,谢礼立,赵桂峰.抗震设防烈度的决策分析方法研究[J].世界地震工程,2007,23(1):86-91.
