基于HOT理论的网络抗毁性动态演化模型

刘媛妮

(重庆邮电大学通信与信息工程学院，重庆 400065)

1 概述

随着自然灾害、恶意攻击等事件对互联网生存性构成的威胁日益增多，提高网络的抗毁性具有重要的研究意义。以往的网络抗毁性研究大都建立在图论基础上，不能很好地把握Internet的拓扑规律和动态行为特性，很难从根本上解决大型复杂网络的抗毁性问题。Internet发展至今，其内在规律在外部则表现为度分布的幂率特性[1-2]，即:()PK=CKλ-× ，其中，P(K)指节点度数为K的概率；C为常数；λ为常数。这种幂率特性并不是偶然出现的，而是其内在的择优选择机制所产生的结果:新节点加入网络时总是倾向于与最“优”的节点相连。从用户角度来讲，其加入网络时将会倾向于选择与具有较高抗攻击能力以及自恢复能力的节点进行连接，以保证自身的安全性；而对于网络中已经存在的节点来说，抗毁性越强的节点获得新节点连接的概率越大。因此，对于网络抗毁性问题的研究，要从网络内部的发展规律出发，通过研究节点在网络中的动态演化行为建立具有抗毁性的网络模型，将是网络抗毁性研究的一条新途径。

HOT[3-4]最优化理论表明，系统在朝最优化方向演化后，其外在特征将会表现出幂率特性。因此，当把建立具有抗毁性的网络模型作为 HOT问题进行求解时，为了真实模拟节点在网络中的演化过程，节点在进行择优选择的过程中，要根据节点的抗攻击能力、自恢复能力、连接能力、传输代价以及连接范围等因素综合考虑最“优”的节点进行连接。这种择优选择的过程不仅使Internet最终在外在形式上表现为节点度符合幂率分布、抗攻击能力等综合特性朝最优化方向发展，从而可以从根本上解决网络性能的优化问题。

本文将建立具有抗毁性的网络动态演化模型作为 HOT问题进行求解，通过模拟单个节点在网络中的产生、成长和消亡过程来建立具有抗毁性的网络动态演化模型，使得建立的模型不仅在节点度分布上与互联网节点度分布呈现幂率特性相一致，而且将抗毁性作为节点择优互联的一个考虑因素，从系统发展的内部演化规律使得模型的抗毁能力朝最优化方向发展。

2 研究现状

研究表明，Internet的节点度分布符合幂率分布(power law)，在这种分布下，网络中大部分节点只有少数连接，而少数节点则拥有大量的连接。HOT理论从系统优化设计的角度说明了幂率特性产生的原因:即全局性的优化过程可导致幂率分布。HOT理论建模是使用一种优化框架来模拟节点在网络中的发展过程，并且以一种增量式优化的方法使系统不断朝最优的方向发展，这种方式是按照网络发展的内部诱因来建模，当网络朝最优化方向发展的过程中，一些外部表现如power law等特征会自然地表现出来，而不是仅关注一些统计特性的显式表现，如节点的层次性、节点度分布等。HOT系统是伴随着使系统故意朝向鲁棒性设置的过程出现的，目的是使系统对不确定性有一定的容忍度(Tolerance)。产量的最优化将会产生高性能以及高的吞吐量以及事件规模的幂率分布和对于不确定性事件的高敏感性。

HOT系统对于系统在设计过程中实现考虑到的因素，具有很强的鲁棒性(high-robust)，但是对于考虑到的因素，有着很强的敏感性(fragile)，也反映了当前复杂系统的 Robust-yet-fragile特性。当前针对HOT理论的应用主要集中于 2个方面:(1)PLR(Probability-Loss-Resource)问题的优化[2]；(2)网络优化建模[5-6]。

文献[5]最先尝试将 Internet建模作为 HOT问题求解。新节点i连接到一个已存在的节点j的依据是2个目标的权重最小，即:

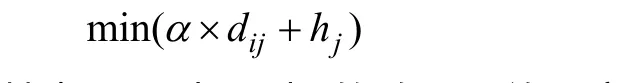
其中，dij为i到j的欧几里德距离；hj是从j到其他所有节点的平均跳数。当α在不同范围内取值时，可以得到星形、指数度分布和幂率度分布3种类型的拓扑[1]。文献[6]等开始尝试应用 HOT理论对 Internet的AS级拓扑进行建模，他们在不同程度上考虑了AS的连接能力、商业关系、连接代价等直观因素，生成的模型在某些特性上与真实拓扑相符合。

3 动态演化模型

3.1 基本定义

通过研究，将网络中的每个节点抽象为一个8元组(i, Ipi, Cci, Cri, Rdi, Sri, Aai, (xi, yi))，其中:

(1)i:区分不同节点的唯一标识。

(2)Ipi:节点的重要性，用于衡量节点在网络中的重要程度。节点i在加入网络时，首先要根据其重要性以确定其连接能力、连接范围等属性，另外节点在网络的动态演化过程中，其重要性将会发生改变。因此，节点i的重要性可以表示为:

其中，Ci为节点 i重要性的常量部分；Bi为节点 i重要性的变量部分；由该节点加入网络后的介数[7-8]决定，α为Ci与Bi之间的调节因子。

(3)Cci:节点的连接能力。节点受其性能限制所能连接的最大数目。重要性越高的节点其连接能力也越高，反之亦然。

(4)Cri:节点的连接半径。在实际情况中，需要考虑连接的可行性，过长的连接需要极高的连接代价，不具备实际意义。因此，节点i的连接范围是以其自身坐标为原点，Cri为半径的圆。

(5)Rdi:节点的度增长率。反映了节点在网络中的增长速度的快慢。在网络中，节点的增长速度并不相同，有些新加入节点在很短时间内即变为度数较大的节点，引入度增长率就是为了正确再现这一现象。在模型中以随机分布的方式为节点设置度增长率。

(6)(xi, yi):节点坐标。节点i在模拟范围内的坐标值。

(7)Sri:节点的自恢复能力。衡量节点在受到攻击后从脱离网络到成功恢复这一能力的大小。在通常情况下，关键节点具有更好的备份措施，因此，重要性越大的节点自恢复的能力更高。

(8)Aai:节点的抗攻击能力。衡量节点对于攻击的抵御能力，通常对于网络中的关键节点，其周围部署的安全工具较之普通节点要多得多，对于一般的攻击抵抗能力也会增高。

3.2 模型建立过程

模型在建立的最初阶段需要在网络中一次性加入m0个节点，随后将以这m0个节点为基础，每一步随机地进行如下的一个操作:

(1)以概率p1加入一个新的节点i，该操作主要分为4步:

1)配置节点i的各种属性。

2)根据 i坐标信息，在其连接范围 Cri内选择一节点j进行连接。新节点j选择与网络中已存在的节点i连接的规则如下:若在节点i的连接范围内不存在这样的节点j，则取消该操作；若存在节点j，则节点j被选择的概率:

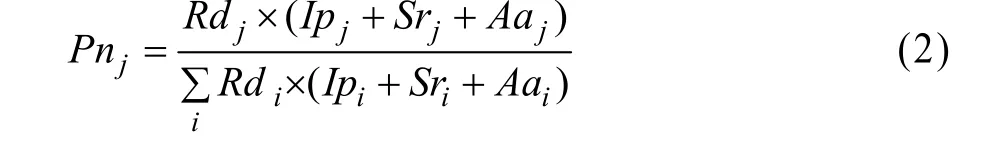
3)将节点 i与被选中的节点 j连接，即加入一条新边 i−j。

4)更新网络信息。由于新加入了节点和边，需对网络中受影响的节点重新计算其各属性值。

(2)以概率 p2加入一条新边:在节点 i和节点 j之间加入新的连接边，主要分为2步:

1)在所有节点中随机选择一节点 i，且满足Ki＜Cci，其中Ki为节点i当前的度数，即在添加边的过程中要保证节点的度数不超过其连接能力。

2)在节点i的连接范围内选择一节点j进行连接。选择j时应满足Ccj＞Cci，同时，节点j被选择的概率应为Pnj。若在i的连接范围内不存在这样的节点j，则操作到此结束。

(3)以概率 p3删除一个已存在的节点，包括 2种情况:

1)永久性删除节点，即节点的正常更替:此操作主要分成2步:

①重要性越小的节点被更替的概率越大。则节点j被删除的概率为:

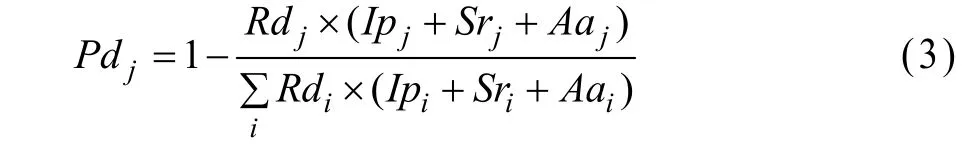
②更新网络信息:对网络中受影响的节点重新计算其各属性值。

2)攻击性删除节点:网络中节点受到攻击，使得节点暂时失效，在这种情况下，节点经过一段时间的自恢复后还会重新加入到网络中。此操作主要分为3步:

①重要性越大的节点被删除的概率越大。则节点j被选择的概率为:

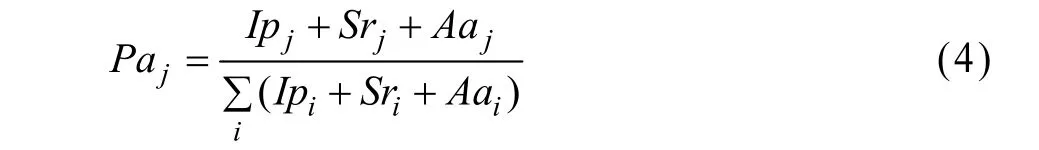
②节点j被选择后，则以概率P判定该次攻击能否成功，若成功，则将节点j以及与其连接的所有边一并删除；若失败，说明节点足以抵御这一次攻击，则操作到此取消。

③若上述攻击成功，则更新网络信息。需对网络中受影响的节点重新计算其各属性值。

(4)以概率p4删除一条已存在的边。

1)在全部节点中随机选择一节点作为 i，设网络全部节点数为x，则i被选中的概率为1/x。在i的所有边中，选择连接的j重要性最小的边进行删除。节点j被选择的概率为Pdj。

2)若删除掉该边之后，i的度变为0，脱离整个网络，则再执行边重连的操作。

4 网络抗毁性动态演化模型分析

本节首先对建立的网络模型的度分布进行分析，然后研究节点的度分布情况，以及在何种情况下会产生节点度符合幂率分布的模型。

4.1 节点度分布分析

在建模时，执行完初始化操作之后，假设余下的4种操作在一个时间步内被执行的概率分别为P1、P2、P3、P4，在删除已有边的过程中又分为以概率 P31永久性删除或者以概率 P32进行攻击性删除，其中，P3=P31+P32。设节点 i加入网络过程中选择节点 j进行连接的概率为 Pnj，永久性删除特定节点 j的概率为Pdj，攻击性删除特定节点 j的概率为Paj，节点 j被攻击成功的概率为p，删除特定边中选择的概率为在网络中全部节点随机选择，即 1/x(x为当前网络中全部节点的个数)，选择j的概率是Pdj，即删除边i−j的概率为 Pdj×(1/x)。

设函数 p(K,ti,t)表示节点i在ti时刻加入域间路由系统，在t时刻节点度数变为K的概率，则:

由连续演化定理，节点度数分布概率为:

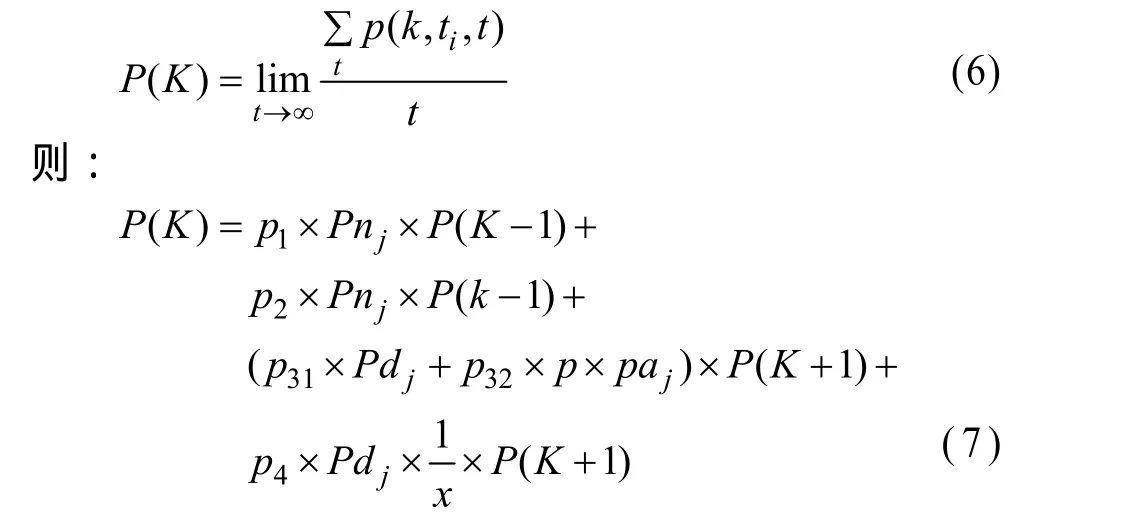
只有在执行了删除节点的操作之后，节点的度数可能变为0，所以:

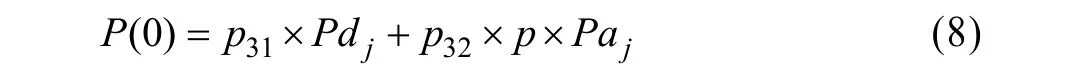
根据概率和为1，即:

由式(7)～式(9)可计算出P(K)的递推公式:

4.2 幂律特性产生条件分析

将式(2)～式(4)代入P(K)的表达式(10)内化简进行分析可得:

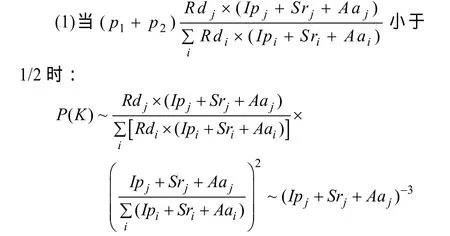
节点度数服从幂指数为3的幂率分布。节点度服从指数分布。

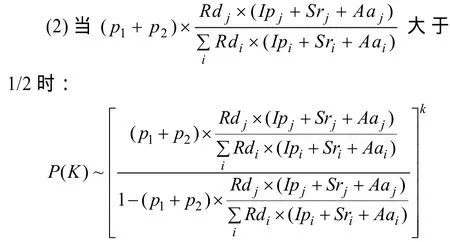
5 仿真分析

本文仿真实验使用负荷-容量模型[9-10]，基于Matlab6.5环境，研究在网络规模同为 1000个节点4413条边，HOT模型和BA模型在发生相继失效的情况下，网络效率E随失效节点数目所占比例P增多时的变化情况。其中，HOT模型中各参数设置如表1所示。

表1 HOT模型各参数值 (%)

通过仿真实验，得到1000个节点的HOT网络模型的节点度分布如图 1所示，其中，直线是P(K )= C× K-3(C为常数)的曲线，散点为HOT模型中节点度的概率分布，由图 1可以看出，HOT模型的度分布与 P(K )= C× K-3的曲线十分接近。

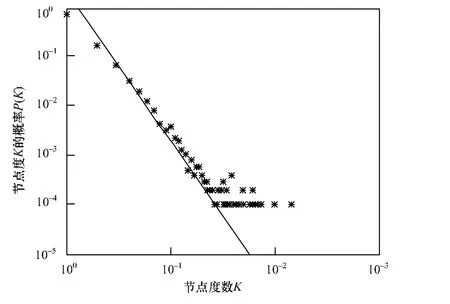
图1 N=1000时的HOT模型节点度分布

为了验证HOT模型的抗毁性，本文在HOT模型以及BA模型上(其中，BA模型的幂指数为−3)研究网络在受到2种不同类型的节点失效后，网络效率E和其初始效率E1之比随着失效节点数目增多时的变化情况，仿真结果如图2所示。图2(a)和图2(b)分别为同等规模的BA和HOT模型在发生相继失效情况下，网络效率E与初始网络效率E1的比值在基于节点度攻击和节点随机失效的情况下随着节点失效数目增多的变化曲线。由图2可以看出，随着节点失效数目的增多，网络效率E不断下降，但是基于HOT模型的网络始终比BA模型具有更高的网络效率比。这说明在同等网络规模、网络受到同等打击的情况下，HOT模型比BA模型的网络效率下降得少，具有更高的抗毁性。

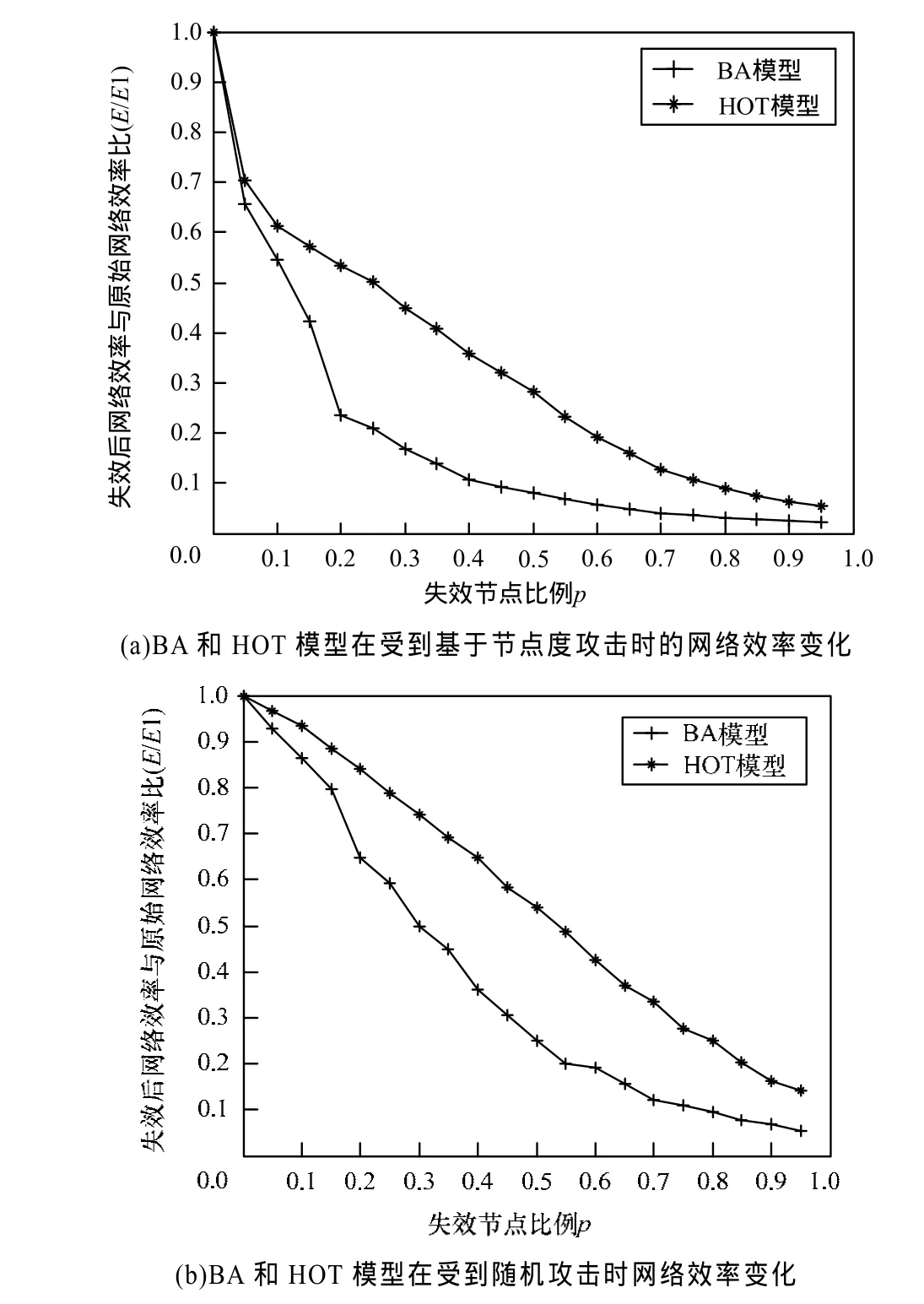
图2 受到不同类型攻击时的网络效率变化曲线

6 结束语

本文以一种优化驱动的方式建立了基于 HOT理论的抗毁性网络动态演化模型，为进行网络抗毁性研究打下了基础。该模型不仅优于传统的图论的建模方法，而且更具真实性。在利用内在规律研究抗毁性网络模型的过程中，可以得出以下结论:网络中各个节点作为独立的系统自主决策，并具有相同的目标，即使自身利益最大化，因此在宏观上具有一致性和可预测性。网络的外在表现是可以调节的，这与其本身的特性并不矛盾；可以通过激励措施引导各个节点进行决策，通过调节节点的不同属性值，可以使系统在整体上表现出期望的特征。

[1]周 苗, 杨家海, 刘洪波, 等.Internet网络拓扑建模[J].软件学报, 2009, 20(1)∶ 109-123.

[2]张 昕, 赵 海, 王莉菲, 等.AS级Internet拓扑分析[J].通信学报, 2008, 29(7)∶ 50-61.

[3]Carlson J M, Doyle J.Highly Optimized Tolerance∶ A Mechanism for Power Laws in Designed Systems[J].Physical Review E, 1999, 60(2)∶ 1412-1427.

[4]Doyle J, Carlson J M, Law P.High Optimized Tolerance,and Generalized Source Coding[J].Physical Review Letters, 2000, 84(24)∶ 5656-5659.

[5]Fabrikant A, Koutsoupias E, Papadimitriou C.Heuristically Optimized Trade-offs∶ A New Paradigm for Power-laws in the Internet[C]//Proc.of ICALP’02.[S.1.]∶IEEE Press, 2002∶ 110-122.

[6]Alderson D, Doyle J, Willinger W.Internet Connectivity at the AS Level∶ An Optimization Driven Modeling Approach[C]//Proc.of ACM SIGCOMM’03.Karlsruhe,Germany∶ ACM Press, 2003.

[7]Freeman L C.A Set of Measures of Centrality Based on Betweenness[J].Sociometry, 1997, 40(1)∶ 35-41.

[8]Brandes U.A Faster Algorithm for Betweenness Centrality[J].Journal of Mathematical Socialogy, 2001,25(2)∶ 163-177.

[9]Kinney R, Crucitti P, Albert R, et al.Modeling Cascading Failures in the North American Power Grid[EB/OL].(2010-10-20).http∶//arXiv∶cond-mat/0410318.

[10]Kinney R, Crucitti P, Albert R, et al.Modeling Cascading Failures in the North American Power Grid[J].European Physical Journal, 2005, 46(1)∶ 101-107.